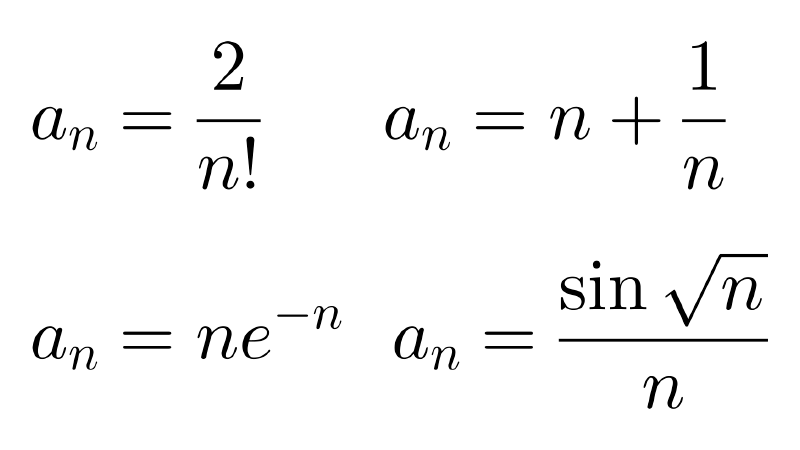
Tipos de sucesiones matemáticas

Daniel Machado · Actualizado el 26/08/2025

Existen diferentes clases de sucesiones matemáticas, las veremos en la siguiente tabla con ejemplos de cada una.

Tipo	Descripción	Ejemplo
Sucesiones finitas	Son aquellas que contienen un número limitado de términos y tienen un último elemento.	(2, 3, 4, 5) (3, 5, 7, 9, 11)
Sucesiones infinitas	Son aquellas que tienen infinitos términos y no poseen un último elemento.	(2, 4, 6, 8, 10, …) (-5, -10, -15, -20, -25, …)
Sucesiones acotadas inferiormente	Son aquellas cuyos términos no son menores que un cierto valor real, llamado cota inferior.	(2, 4, 6, 8, 10, …) tiene como cota inferior a 2.
Sucesiones acotadas superiormente	Son aquellas cuyos términos no superan un cierto valor real, llamado cota superior	(-1, -2, -3, -4, …) tiene como cota superior a -1.
Sucesiones acotadas	Son aquellas que están acotadas tanto superior como inferiormente, es decir, todos sus términos se encuentran entre dos valores reales.	(1, 1/2, 1/3, 1/4, 1/5, 1/6, …) tiene todos sus términos entre 0 y 1.
Sucesiones crecientes	Son aquellas en las que cada término es mayor o igual que el anterior.	(1, 2, 2, 3, 3, …)
Sucesiones estrictamente crecientes	Son aquellas en las que cada término es estrictamente mayor que el anterior, sin repeticiones.	(1, 3, 5, 7, 9, 11, …)
Sucesiones decrecientes	Son aquellas en las que cada término es menor o igual que el anterior.	(10, 8, 8, 5, 2, …)
Sucesiones estrictamente decrecientes	Son aquellas en las que cada término es menor que el anterior, sin repeticiones.	(15, 10, 5, 0, -5, …)
Sucesiones monótonas	Son aquellas que mantienen siempre la misma tendencia (creciente o decreciente) a lo largo de todos sus términos.	(1, 3, 5, 7, 9, 11, …) (20, 15, 10, 5, 0, …)
Sucesiones constantes	Todos sus términos son iguales: a_n = k siendo k un número real.	(5, 5, 5, 5, 5, …) (-1, -1, -1, -1, …)
Sucesiones iguales	Dos sucesiones son iguales si coinciden término a término.	(a_n = 2n) y (b_n = n + n) son la misma sucesión: (2, 4, 6, 8, 10, …)
Sucesiones convergentes	Son aquellas que tienen límite finito. Sus valores se acercan cada vez más a un número fijo a medida que avanzamos en los términos.	(1, 1/2, 1/3, 1/4, 1/5, 1/6, …) converge a 0. (1/2, 2/3, 3/4, 4/5, 5/6, 6/7, …) converge a 1.
Sucesiones divergentes	Son aquellas que no son convergentes. Pueden tener límite infinito o ser oscilantes.	La sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, …) es divergente porque crece sin límite. (1, -1, 1, -1, 1, -1, …) es divergente porque es oscilante.
Sucesiones oscilantes	Son aquellas que no tienen límite finito ni infinito, por tanto, son divergentes.	(1, 2, 3, 1, 2, 3, …) (-1, 1, -1, 1, -1, 1, ...) (0, 1, 0, 2, 0, 3, 0, 4, …)
Sucesiones alternantes	Son aquellas cuyos términos cambian de signo en forma sucesiva, es decir, positivos y negativos se intercalan. Estas sucesiones pueden converger o no.	(-2, 2, -2, 2, -2, …) es alternante y divergente. (a_n = (-1)ⁿ/ n) es alternante y converge a cero.
Sucesiones o progresiones aritméticas	Son aquellas en las que cada término se obtiene sumando o restando una misma cantidad constante, llamada diferencia común, al término anterior.	(2, 5, 8, 11, 14, …) con diferencia 3 (10, 6, 2, -2, -6, …) con diferencia -4.
Sucesiones o progresiones geométricas	Son aquellas en las que cada término se obtiene multiplicando o dividiendo el término anterior por una misma cantidad constante, llamada razón común.	(3, 6, 12, 24, 48, …) con razón 2. (81, 27, 9, 3, 1, …) con razón 1/3.
Sucesiones cuadráticas	Son aquellas en las que la diferencia entre términos consecutivos no es constante, pero la segunda diferencia (diferencia de las diferencias) sí lo es, y cuyos términos pueden expresarse mediante una fórmula cuadrática del tipo a_n = an² + bn + c.	(1, 4, 9, 16, 25, …) con a_n = n² (2, 5, 10, 17, 26, …) con a_n = n² + 1

Tipos de sucesiones numéricas con ejemplos

Bibliografía

Apostol, T. (1984). Calculus: Cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15.ª ed.). El Ateneo.
Stewart, J. (2012). Cálculo de una variable: Trascendentes tempranas (7.ª ed.). Cengage Learning.
Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: Matemáticas para el cálculo (6.ª ed.). Cengage Learning.
Zill, D. y Wright, W. (2011). Cálculo: Trascendentes tempranas (4.ª ed.). McGraw-Hill Education.