Sucesión convergente
Una sucesión convergente es una secuencia de números cuyos valores se aproximan cada vez más a un valor fijo a medida que la sucesión avanza hacia el infinito. A este valor lo llamamos límite de la sucesión. Una sucesión que no es convergente se llama divergente.
Ejemplos
- La sucesión ( 1/n2 ) = (1, 1/4, 1/9, 1/16, 1/25, …) converge a cero porque sus términos se acercan cada vez más a ese valor a medida que n se hace grande.
- La secuencia ( (n + 1) / n ) = (2, 3/2, 4/3, 5/4, 6/5, …) converge a 1 ya que los valores de sus términos se aproximan a ese valor cuanto más avanzamos en la sucesión.
- La sucesión constante (3, 3, 3, 3, 3, …) converge a 3 porque todos sus términos son iguales.
- La secuencia ( (-1)n / n ) = (-1, 1/2, -1/3, 1/4, -1/5, …) converge a 0.
- La sucesión de números pares (2, 4, 6, 8, 10, 12, …) no converge porque sus términos crecen sin límite sin acercarse a ningún valor particular.
- La sucesión ( (-1)n ) = ( -1, 1, -1, 1, -1, …) no es convergente porque sus términos no se acercan a ningún valor sino que "saltan" continuamente entre dos valores.
Índice
Definición formal
De forma estricta, una sucesión se considera convergente cuando posee un límite finito. Dicho de otro modo, existe un número real L tal que los términos de la sucesión se aproximan a él a medida que avanzamos hacia índices cada vez mayores.
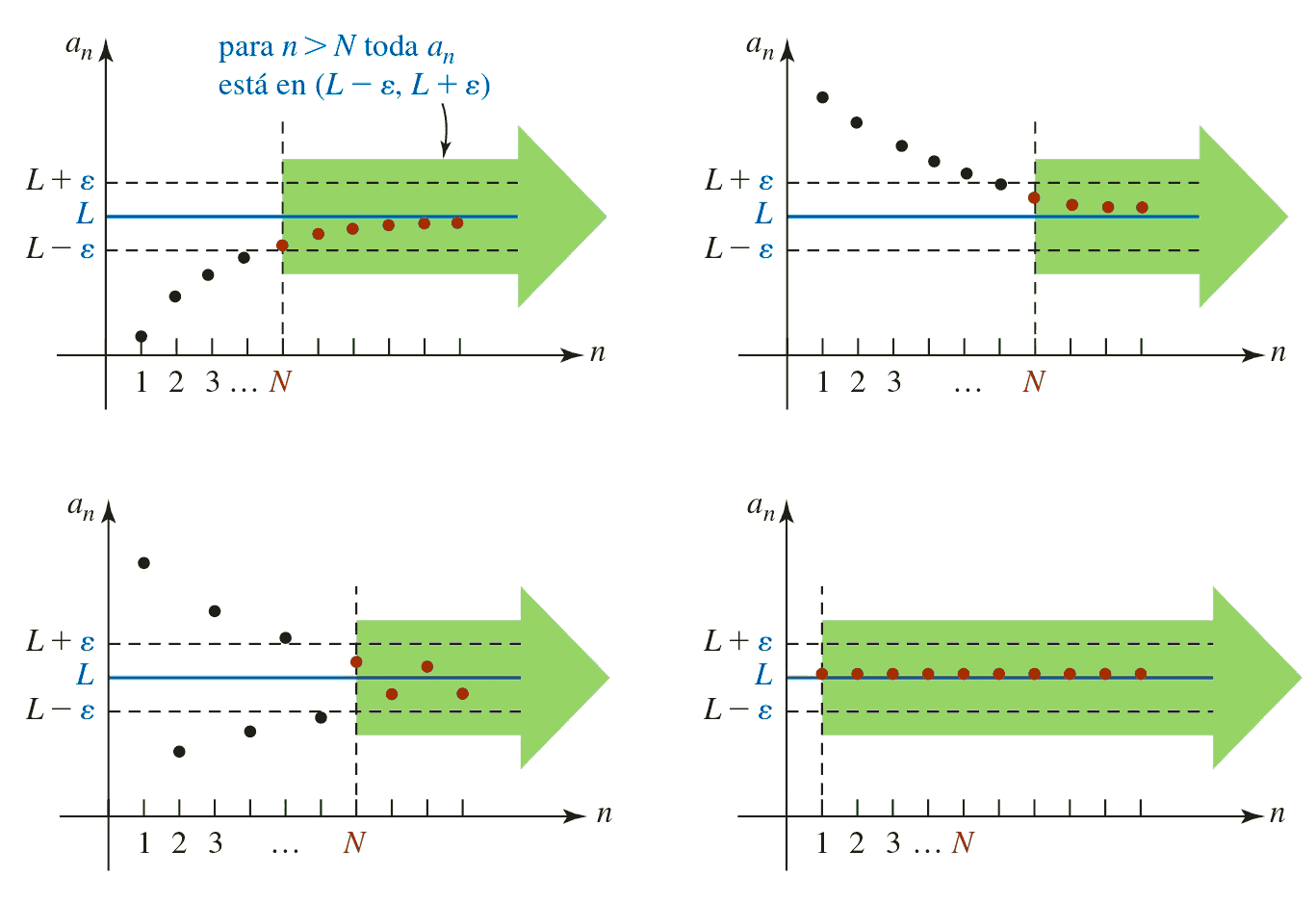
Formalmente, diremos que una sucesión (an) converge a L si, para todo número positivo ε, por pequeño que sea, podemos encontrar un entero natural N tal que se cumpla:
|an - L| < ε para todo n > N
En este caso, L recibe el nombre de límite de la sucesión y se denota como:
\(\lim_{n \to \infty} a_n=L\)
o también
\(a_n \to L \quad \text{cuando } n \to \infty\)
Si no existe tal número L, diremos que la sucesión es divergente. Si una sucesión converge, su límite es único.
Si la notación simbólica te resulta difícil de entender, puedes consultar el artículo sobre límite de una sucesión donde explicamos en detalle qué significan ε y N y cómo interpretarlos.
Toda sucesión que no es convergente se llama divergente. Una sucesión puede diverger por dos motivos:
- Sus términos crecen en valor absoluto sin acercarse a ningún número. En este caso se dice que el límite es infinito (si los términos crecen en sentido positivo) o menos infinito (si los términos se hacen cada vez más negativos).
- Sus términos oscilan entre distintos valores sin acercarse a ningún valor fijo. En este caso se dice que el límite no es finito ni infinito.
Importante: decir que el límite es infinito (o menos infinito) no significa que el límite exista. Estos términos se usan para describir el comportamiento de la sucesión, es decir, se trata de expresar de qué forma no existe el límite: sus términos crecen en valor absoluto sin ninguna cota.
Cómo saber si una sucesión es convergente
La forma más directa de probar si una sucesión es convergente es calcular su límite cuando n tiende a infinito. Si el resultado es un número real finito, la sucesión converge a ese número. Si el resultado es infinito o no existe, la sucesión es divergente.
Ejemplo
Determinar si las sucesiones definidas por los siguientes términos generales son convergentes o divergentes.
- \(a_n=\dfrac{2n}{n+1}\)
- \(a_n=3+(-1)^n\)
- \(a_n=\dfrac{4n^2-1}{2n^2+3}\)
- \(a_n=\dfrac{n^2}{2^n-1} \)
- \(a_n=\sqrt{n^2+3n-1}\)
- \(a_n=\sin(n\pi)\)
Soluciones
Solución 1
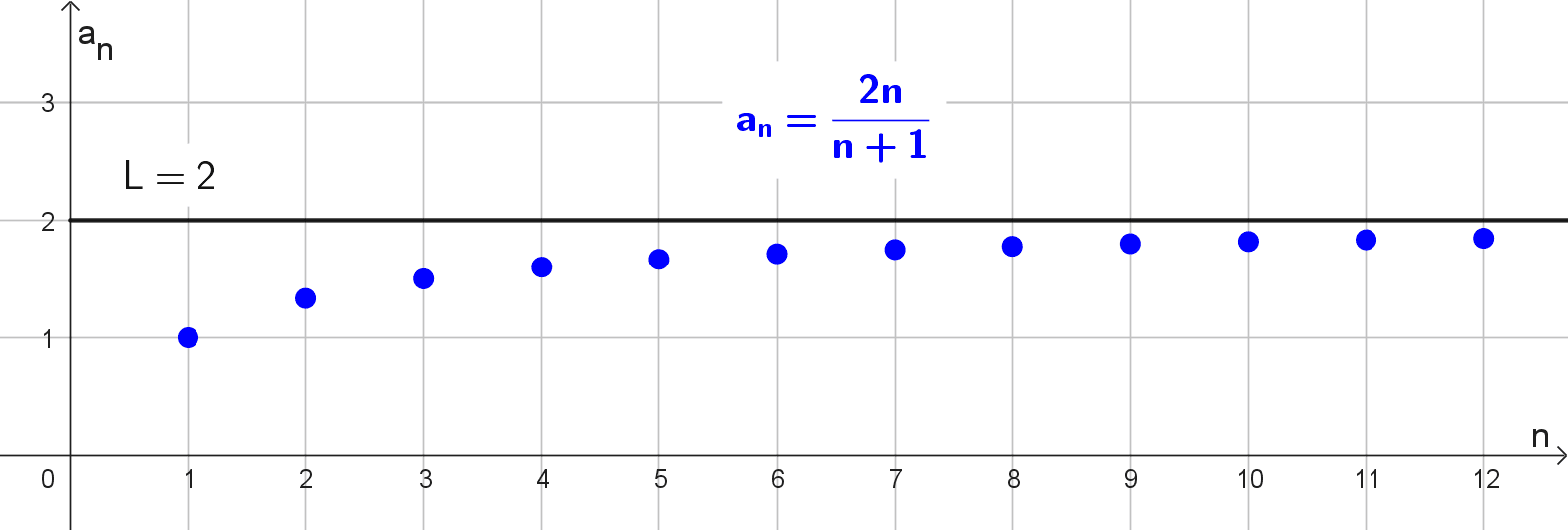
Para determinar si la sucesión definida por el término general \(a_n=\dfrac{2n}{n+1}\) es convergente o divergente, primero calculamos algunos de sus términos para observar su comportamiento. Sustituimos los primeros valores de \(n\) y obtenemos:
\(a_1=\dfrac{2(1)}{1+1}=\dfrac{2}{2}=1\)
\(a_2=\dfrac{2(2)}{2+1}=\dfrac{4}{3} ≈ 1,33\)
\(a_3=\dfrac{2(3)}{3+1}=\dfrac{6}{4}=1,5\)
\(a_4=\dfrac{2(4)}{4+1}=\dfrac{8}{5}=1,6\)
\(a_5=\dfrac{2(5)}{5+1}=\dfrac{10}{6} ≈ 1,67\)
\(a_{10}=\dfrac{2(10)}{10+1}=\dfrac{20}{11} ≈ 1,82\)
\(a_{100}=\dfrac{2(100)}{100+1}=\dfrac{200}{101} ≈ 1,98\)
Al observar estos valores, podemos predecir que la sucesión parece estar convergiendo hacia el número 2. Este comportamiento también se puede ver en la gráfica de la sucesión.
Para confirmar la convergencia, calculamos el límite cuando n tiende a infinito. La estrategia para resolver este tipo de límites de sucesiones racionales donde el numerador y el denominador tienden a infinito (una indeterminación del tipo \(\infty /\infty\)) es dividir tanto el numerador como el denominador por la potencia más alta de \(n\) que aparece en la expresión, que en este caso es \(n.\)
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{2n}{n+1}=\lim_{n \to \infty} \dfrac{\dfrac{2n}{n}}{\dfrac{n}{n}+\dfrac{1}{n}}=\lim_{n \to \infty} \dfrac{2}{1+\dfrac{1}{n}}\)
Ahora, analizamos el comportamiento de cada término por separado cuando \(n \to \infty.\) El numerador es la constante 2. En el denominador, el número 1 es constante y el término \(\dfrac{1}{n}\) tiende a 0. Por lo tanto, el límite de todo el denominador es \(1+0=1.\)
\(\lim_{n \to \infty} a_n=\dfrac{2}{1}=2\)
Dado que el límite existe y es un número real finito, podemos concluir que la sucesión dada es convergente.
Solución 2
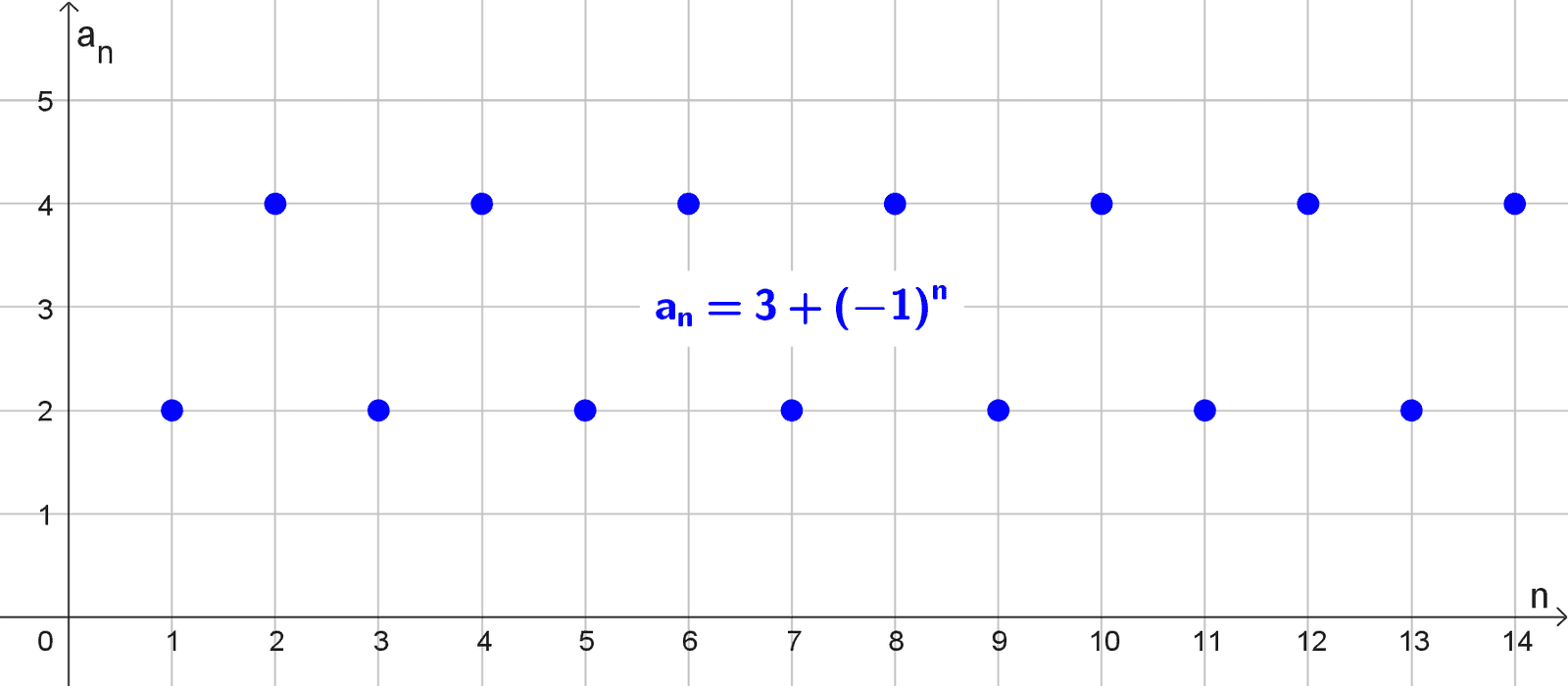
Para analizar la convergencia de la sucesión definida por \(a_n=3+(-1)^n,\) calculamos algunos de sus términos para observar su comportamiento. Sustituimos los primeros valores de \(n\) y obtenemos:
\(a_1=3+(-1)^1=3-1=2\)
\(a_2=3+(-1)^2=3+1=4\)
\(a_3=3+(-1)^3=3-1=2\)
\(a_4=3+(-1)^4=3+1=4\)
\(a_5=3+(-1)^5=3-1=2\)
\(a_{10}=3+(-1)^{10}=3+1=4\)
\(a_{11}=3+(-1)^{11}=3-1=2\)
Al examinar estos valores, notamos que la sucesión oscila de manera constante entre 2 (cuando n es impar) y 4 (cuando n es par). Esta oscilación indica que los términos no se acercan a un único valor fijo a medida que n aumenta. Por lo tanto, el límite no existe, y concluimos que la sucesión es divergente por oscilación.
Solución 3
Para determinar si la sucesión \(a_n=\dfrac{4n^2-1}{2n^2+3}\) converge o diverge, primero evaluamos algunos términos para intuir su comportamiento. Calculamos:
\(a_1=\dfrac{4(1)^2-1}{2(1)^2+3}=\dfrac{3}{5}=0,6\)
\(a_2=\dfrac{4(4)-1}{2(4)+3}=\dfrac{15}{11} ≈ 1,36\)
\(a_3=\dfrac{4(9)-1}{2(9)+3}=\dfrac{35}{21} ≈ 1,67\)
\(a_4=\dfrac{4(16)-1}{2(16)+3}=\dfrac{63}{35}=1,8\)
\(a_5=\dfrac{4(25)-1}{2(25)+3}=\dfrac{99}{53} ≈ 1,87\)
\(a_{10}=\dfrac{4(100)-1}{2(100)+3}=\dfrac{399}{203} ≈ 1,97\)
\(a_{100}=\dfrac{4(10000)-1}{2(10000)+3}=\dfrac{39999}{20003} ≈ 1,999\)
Estos valores sugieren que la sucesión se aproxima a 2. Para verificarlo, calculamos el límite cuando \(n \to \infty.\) Dado que tanto el numerador como el denominador tienden a infinito (indeterminación \(\dfrac{\infty}{\infty}\)), dividimos ambos por \(n^2,\) la potencia dominante:
\(\lim_{n \to \infty} \dfrac{4n^2-1}{2n^2+3}=\lim_{n \to \infty} \dfrac{\dfrac{4n^2}{n^2}-\dfrac{1}{n^2}}{\dfrac{2n^2}{n^2}+\dfrac{3}{n^2}}=\lim_{n \to \infty} \dfrac{4-\dfrac{1}{n^2}}{2+\dfrac{3}{n^2}}\)
Cuando \(n \to \infty,\) los términos \(\dfrac{1}{n^2}\) y \(\dfrac{3}{n^2}\) tienden a 0. Así, el límite es:
\(\lim_{n \to \infty} \dfrac{4-\dfrac{1}{n^2}}{2+\dfrac{3}{n^2}}=\dfrac{4-0}{2+0}=\dfrac{4}{2}=2\)
Como el límite existe y es finito, la sucesión es convergente.
Solución 4
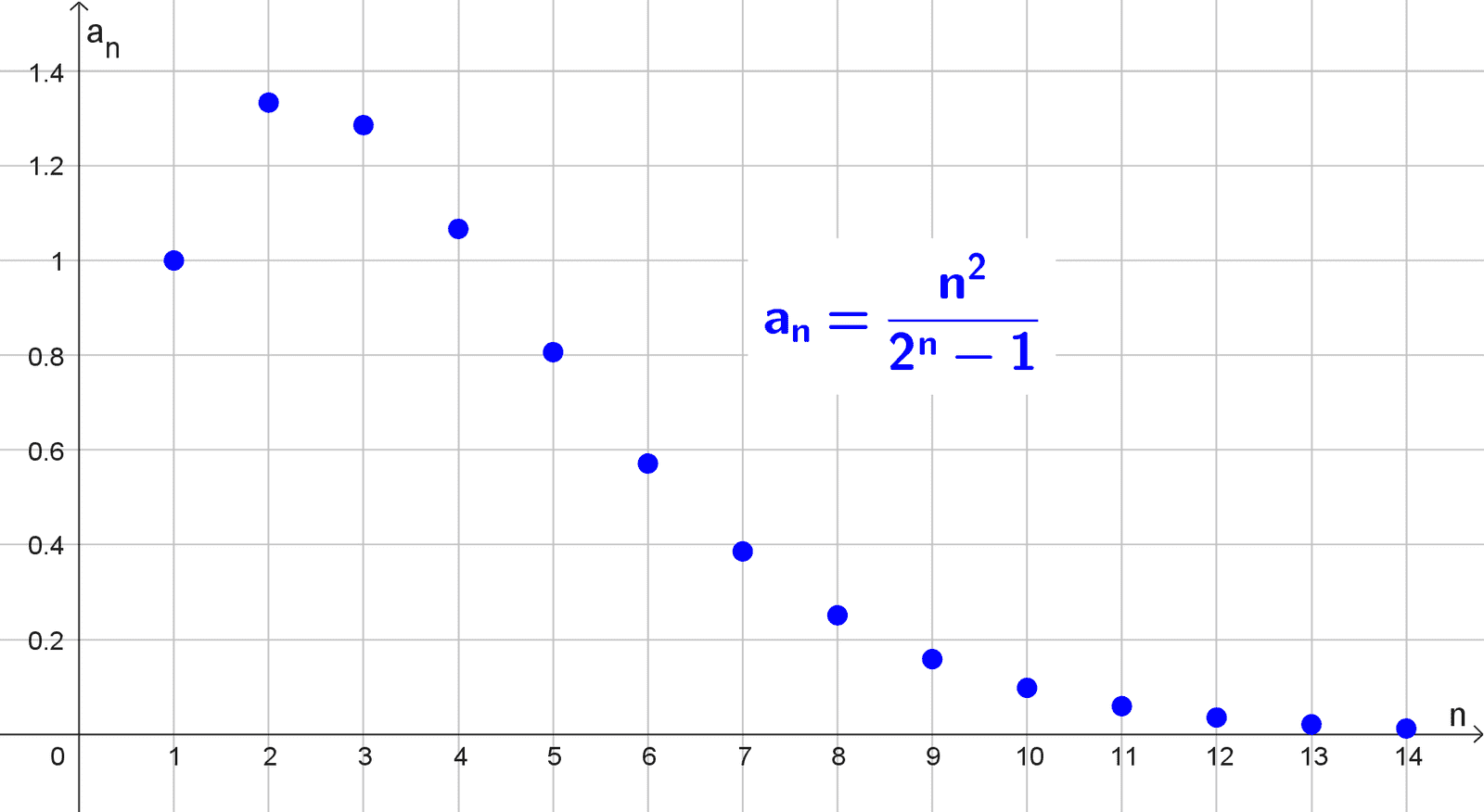
Para analizar la sucesión \(a_n=\dfrac{n^2}{2^n-1},\) calculamos términos iniciales para observar su tendencia:
\(a_1=\dfrac{1^2}{2^1-1}=\dfrac{1}{1}=1\)
\(a_2=\dfrac{4}{4-1}=\dfrac{4}{3} ≈ 1,33\)
\(a_3=\dfrac{9}{8-1}=\dfrac{9}{7} ≈ 1,29\)
\(a_4=\dfrac{16}{16-1}=\dfrac{16}{15} ≈ 1,07\)
\(a_5=\dfrac{25}{32-1}=\dfrac{25}{31} ≈ 0,81\)
\(a_6=\dfrac{36}{64-1}=\dfrac{36}{63} ≈ 0,57\)
\(a_{10}=\dfrac{100}{1024-1}=\dfrac{100}{1023} ≈ 0,098\)
\(a_{20}=\dfrac{400}{1048576-1} ≈ \dfrac{400}{1048575} ≈ 0,00038\)
Los valores decrecen rápidamente después de \(n=4,\) sugiriendo convergencia a 0. La función exponencial \(2^n\), por tener base mayor a 1, crece mucho más rápido que cualquier polinomio (como \(n^2\)), por lo que el denominador domina al numerador. Así, la sucesión converge a 0.
\(\lim_{n \to \infty} \dfrac{n^2}{2^n-1}=0\)
Solución 5
Para estudiar el comportamiento de la sucesión definida por \(a_n=\sqrt{n^2+3n-1},\) comenzamos calculando algunos de sus términos para observar su tendencia. Evaluamos:
\(a_1=\sqrt{1^2+3(1)-1}=\sqrt{1+3-1}=\sqrt{3} ≈ 1,73\)
\(a_2=\sqrt{4+6-1}=\sqrt{9}=3\)
\(a_3=\sqrt{9+9-1}=\sqrt{17} ≈ 4,12\)
\(a_4=\sqrt{16+12-1}=\sqrt{27} ≈ 5,20\)
\(a_5=\sqrt{25+15-1}=\sqrt{39} ≈ 6,24\)
\(a_{10}=\sqrt{100+30-1}=\sqrt{129} ≈ 11,36\)
\(a_{100}=\sqrt{10000+300-1}=\sqrt{10299} ≈ 101,48\)
Estos valores muestran un crecimiento continuo y sin cota aparente, lo que sugiere que la sucesión diverge a infinito. Para confirmarlo, calculamos el límite cuando \(n \to \infty.\) Notamos que la expresión dentro de la raíz cuadrada es un polinomio de grado 2, por lo que el término dominante es \(n^2.\) Podemos reescribir la expresión para analizar su comportamiento:
\(a_n=\sqrt{n^2+3n-1}=\sqrt{n^2 \left(1+\dfrac{3}{n}-\dfrac{1}{n^2}\right)}=n \cdot \sqrt{1+\dfrac{3}{n}-\dfrac{1}{n^2}}\)
Ahora, tomamos el límite:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \left(n \cdot \sqrt{1+\dfrac{3}{n}-\dfrac{1}{n^2}} \right)\)
Cuando \(n \to \infty,\) los términos \(\dfrac{3}{n}\) y \(\dfrac{1}{n^2}\) tienden a 0, por lo que la expresión bajo la raíz converge a 1. Así, tenemos:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} n \cdot 1=\infty\)
Dado que el límite no es finito y la sucesión crece indefinidamente, concluimos que diverge a infinito.
Solución 6
Para determinar la convergencia de la sucesión \(a_n=\sin(n\pi),\) evaluamos sus primeros términos para identificar algún patrón.
\(a_1=\sin(1 \cdot \pi)=\sin(\pi)=0\)
\(a_2=\sin(2\pi)=0\)
\(a_3=\sin(3\pi)=0\)
\(a_4=\sin(4\pi)=0\)
\(a_5=\sin(5\pi)=0\)
\(a_{10}=\sin(10\pi)=0\)
\(a_{100}=\sin(100\pi)=0\)
Todos los términos son exactamente 0, sin excepción, ya el seno de cualquier múltiplo entero de \(\pi\) es 0. Por tanto, la sucesión es constante e igual a 0 para todo \(n.\) Al ser constante, su límite cuando \(n \to \infty\) es trivialmente 0:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} 0=0\)
Como el límite existe y es finito, la sucesión es convergente.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Límites de sucesiones conocidas
- Sucesión constante: \(\lim_{n \to \infty} k=k\) para todo número real k.
- Sucesión inversa de una potencia: \(\lim_{n \to \infty} \dfrac{1}{n^r}=0\) si r > 0. Si r < 0 la sucesión diverge a infinito.
- Progresión geométrica: \(\lim_{n \to \infty} r^n=0\) si |r| < 1. Si |r| > 1 la sucesión diverge a infinito.
- Logaritmo sobre potencia: \(\lim_{n \to \infty} \dfrac{(\log n)^a}{n^b}=0\) para todo a > 0, b > 0.
- Raíz enésima de n: \(\lim_{n \to \infty} \sqrt[n]{n}=1\)
- Número e: \(\lim_{n \to \infty} \left(1+\dfrac{a}{n}\right)^n=e^a\) para todo real a, siendo e el número de Euler.
Criterios de convergencia de sucesiones
Otra forma de determinar si una sucesión converge es utilizando algún criterio de convergencia, veremos los más importantes a continuación.
Teorema de la sucesión monótona
Toda sucesión monótona y acotada es convergente.
Una sucesión monótona es aquella cuyos términos son siempre crecientes o siempre decrecientes. Una sucesión acotada es aquella cuyos términos permanecen dentro de un intervalo fijo, es decir, no sobrepasan ciertos valores máximo y mínimo.
Este teorema no nos indica a qué número converge la sucesión, sólo asegura que el límite existe. Es importante destacar que esta condición es suficiente, pero no necesaria. Esto significa que:
- Una sucesión puede estar acotada y no converger. Por ejemplo, \(((-1)^n)\) está acotada entre -1 y 1, pero no converge porque oscila indefinidamente.
- Una sucesión puede no ser monótona y aun así converger. Por ejemplo, \(\left(\dfrac{(-1)^n}{n}\right)\) no es monótona, pero converge a 0.
- Una sucesión puede ser monótona pero no convergerá si no está acotada. Por ejemplo, \((a_n=n)\) es monótona creciente pero no converge, sino que tiende a infinito.
Por otro lado, toda sucesión convergente debe ser acotada. En otras palabras, la acotación es una condición necesaria para la convergencia, pero no suficiente por sí sola. En la siguiente tabla se resume el razonamiento.
| Monótona | Acotada | ¿Converge? |
|---|---|---|
| Si | Si | Siempre |
| Si | No | Nunca |
| No | Si | A veces |
| No | No | Nunca |
Demostración del teorema
Intuitivamente, si una sucesión crece pero no puede superar cierto techo, cada vez que avanzamos se queda más "pegada" al menor de esos techos posibles; ese techo ideal es el supremo del conjunto de términos y la sucesión tiende a él. De forma análoga, si decrece pero no baja de cierto piso, se aproxima al ínfimo. La completitud de \(\mathbb{R}\) garantiza que ese supremo o ínfimo existe y la monotonía obliga a los términos a acercarse a él.
Ahora haremos la demostración formal para el caso monótona creciente y acotada (el caso decreciente es análogo, invirtiendo las desigualdades y usando el ínfimo).
Sea \((a_n)\) una sucesión con \(a_n \le a_{n+1}\) para todo \(n\) y supongamos que existe \(M\in\mathbb{R}\) tal que \(a_n \le M\) para todo \(n.\) Consideremos el conjunto \(A=\{a_n: n \in\mathbb{N}\}.\) Como A está acotado superiormente, por la propiedad de completitud de \(\mathbb{R}\) existe el supremo \(L=\sup A.\)
Queremos probar que \(\lim_{n\to\infty} a_n=L.\) Sea \(\varepsilon>0.\) Por la definición de supremo, \(L-\varepsilon\) no puede ser cota superior de \(A;\) por tanto existe algún término \(a_N\in A\) tal que \(a_N>L-\varepsilon.\) Dado que la sucesión es creciente, para todo \(n\ge N\) se cumple \(a_n\ge a_N,\) y por ser \(L\) cota superior de \(A\) también se cumple \(a_n\le L.\) De aquí obtenemos que para todo \(n\ge N\)
\(L-\epsilon<a_n \leq L<L+\epsilon → -\epsilon<a_n-L<\epsilon\)
Por propiedades del valor absoluto, esto es: \(|a_n-L|<\epsilon.\) Como la elección de \(\epsilon>0\) fue arbitraria, esto demuestra que \(\lim_{n\to\infty} a_n=L.\)
El argumento inverso funciona igual para una sucesión monótona decreciente y acotada inferiormente: tomando \(l=\inf\{a_n\}\) y, para dado \(\epsilon>0,\) usando que \(l+\epsilon\) no es cota inferior, se consigue un índice a partir del cual \(l\le a_n<l+\varepsilon,\) lo que muestra \(\lim_{n\to\infty} a_n=l.\) Con esto queda probado que toda sucesión monótona y acotada es convergente.
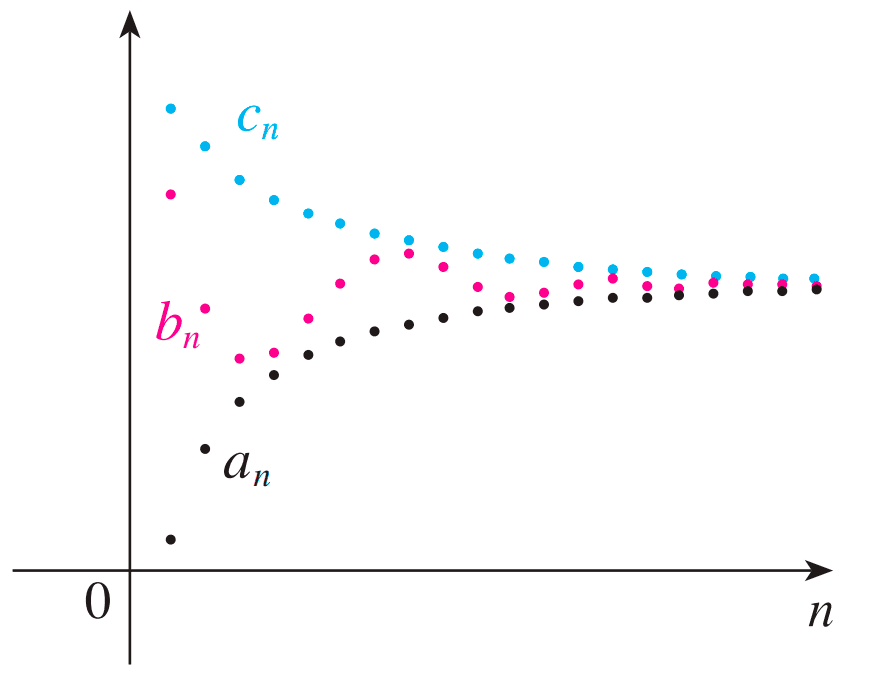
Teorema de compresión (o del sándwich)
Suponga que (an), (bn) y (cn) son sucesiones tales que an ≤ cn ≤ bn para todos los valores de n mayores que algún índice N (esto es, n > N). Si (an) y (bn) convergen a un límite común L, entonces (cn) también converge a L.
Teorema del valor absoluto
Si la sucesión de valores absolutos (|an|) converge a 0, entonces la sucesión (an) converge a 0.
Demostración del teorema
Supongamos que \(|a_n|\to 0.\) Por la definición de límite esto significa que para todo ε > 0 existe un \(N\in\mathbb{N}\) tal que, para todo n > N, se cumple
\(||a_n|-0|<ε\)
Pero \(||a_n|-0|=|a_n|,\) así que para todo n > N tenemos \(|a_n|<ε.\) Eso es exactamente la condición \(|a_n-0|<ε,\) por lo tanto \(a_n\to 0.\)
Una prueba alternativa utilizando el teorema del sándwich consiste en observar que siempre se cumple que:
\(-|a_n|≤ a_n≤|a_n|\)
Si \(|a_n|\to 0,\) las dos sucesiones límite de los extremos son 0; por el teorema de compresión la sucesión intermedia \(a_n\) también debe tender a 0.
Teorema de la función continua
Si acoplamos una función continua a los términos de una sucesión convergente, el resultado también es convergente. Si \(\lim_{n\to \infty} a_n=L\) y la función f es continua en L, entonces \(\lim_{n\to \infty} f(a_n)=f(L)\)
Puedes ver ejemplos de aplicación del teorema de compresión, del valor absoluto y de la función continua en el artículo de límite de una sucesión.
Convergencia de subsucesiones
Una subsucesión de una sucesión \((a_n)\) es una nueva sucesión que se obtiene tomando solo algunos términos de \((a_n),\) respetando el orden original, pero no necesariamente tomándolos todos. Formalmente, si \((n_k)\) es una sucesión estrictamente creciente de índices naturales, la sucesión \((a_{n_k})\) se llama subsucesión de \((a_n).\)
Teorema: si una sucesión converge, entonces todas sus subsucesiones también convergen al mismo límite. Esto es, si \(\lim_{n \to \infty} a_n=L,\) entonces para toda subsucesión \((a_{n_k})\) se cumple \(\lim_{k \to \infty} a_{n_k}=L.\)
Si dos subsucesiones diferentes convergen a límites distintos, entonces la sucesión original no converge. Simbólicamente, si existen dos subsucesiones \((a_{n_k})\) y \((a_{m_k})\) tales que
\(\lim_{k \to \infty} a_{n_k}=L_1 \quad \text{y} \quad \lim_{k \to \infty} a_{m_k}=L_2 \quad \text{con} \quad L_1 \neq L_2\)
entonces la sucesión original \((a_n)\) no converge.
Este resultado se aplica buscando dos subsucesiones con límites distintos: si se encuentran, queda demostrado que la sucesión original no puede tener un único límite y, por lo tanto, no es convergente.
Ejemplo
Consideramos la sucesión \(a_n = (-1)^n\). Tomemos las subsucesiones para índices pares \((a_{2k}) = ((-1)^{2k}) = (1, 1, 1,...)\) y para índices impares \((a_{2k-1}) = ((-1)^{2k-1}) = (-1, -1, -1,...)\). La primera subsucesión converge a 1 y la segunda a -1. Como estos límites son distintos, concluimos que la sucesión original \(a_n\) no converge.
Convergencia de sucesiones recurrentes
Cuando una sucesión está definida por recurrencia, para probar que es convergente normalmente se demuestra primero que es monótona y acotada, de modo que se garantiza su convergencia. Luego, para hallar su límite L se suele suponer que \(\lim_{n\to\infty} a_n=L\) y reemplazar an y an+1 por L en la ecuación de recurrencia, resolviendo la ecuación resultante para obtener el valor de L.
Ejemplo
Probaremos si la siguiente sucesión es convergente:
\(a_{n+1}=\sqrt{2+a_n}\) con \(a_1=\sqrt{2}\)
Primero verificamos que es monótona y acotada. Calculando los primeros términos: \(a_1=\sqrt{2} ≈ 1.414\)
\(a_2=\sqrt{2+\sqrt{2}}≈1.848\)
\(a_3 ≈ 1.961\)
Observamos que la sucesión parece creciente, y se puede demostrar por inducción que para toda n se cumple que \(a_{n+1}>a_n:\)
Para \(n=1,\) tenemos \(a_2=\sqrt{2+\sqrt{2}},\) y como \(\sqrt{2+\sqrt{2}}>\sqrt{2},\) se cumple \(a_2>a_1.\)
Ahora, suponemos que para algún \(k \geq 1\), \(a_{k+1}>a_k\) (hipótesis inductiva). Demostramos que \(a_{k+2}>a_{k+1}.\) Por definición, \(a_{k+2}=\sqrt{2+a_{k+1}}\) y \(a_{k+1}=\sqrt{2+a_k}.\)
Por la hipótesis inductiva, \(a_{k+1}>a_k,\) luego \(2+a_{k+1}>2+a_k,\) y tomando raíces cuadradas (que preservan el orden por ser funciones crecientes), obtenemos \(\sqrt{2+a_{k+1}}>\sqrt{2+a_k}\)
es decir:
\(a_{k+2}>a_{k+1}\)
Así, por inducción, la sucesión \(\{a_n\}\) es creciente para todo \(n \geq 1.\)
Además, por inducción, se puede probar que \(a_n<2\) para todo \(n,\) lo que implica que está acotada superiormente.
Para \(n=1,\) tenemos \(a_1=\sqrt{2} \leq 2,\) lo cual es cierto.
Supongamos ahora que para algún \(k \geq 1,\) se cumple \(a_k \leq 2\) (hipótesis inductiva).
Demostramos que \(a_{k+1} \leq 2.\) Por definición, \(a_{k+1}=\sqrt{2+a_k}.\) Usando la hipótesis inductiva, \(a_k \leq 2,\) luego \(2+a_k \leq 4,\) y tomando raíces cuadradas obtenemos
\(\sqrt{2+a_k} \leq 2\)
Por lo tanto:
\(a_{k+1} \leq 2\)
Hemos probado que la sucesión es creciente (por el resultado anterior) y está acotada superiormente por 2. Además, como \(a_n \geq \sqrt{2}\) (pues es creciente y \(a_1=\sqrt{2}\)), la sucesión también está acotada inferiormente.
Como la sucesión es creciente y acotada, por el teorema de convergencia monótona, es convergente. Si la sucesión converge a \(L,\) entonces \(\lim_{n \to \infty} a_{n+1}=\lim_{n \to \infty} a_n=L\) (esta propiedad se demostrará más adelante en este artículo).
Aplicando el límite en la relación de recurrencia:
\(\lim_{n \to \infty} a_{n+1}=L\)
\(\lim_{n \to \infty} \sqrt{2+a_n}=L\)
\(\sqrt{2+L}=L\)
Elevando al cuadrado y acomodando obtenemos la ecuación cuadrática
\(L^2-L-2=0\)
Las soluciones son L = 2 y L = -1. Descartamos L = -1 porque \(a_n \geq 0.\) Por lo tanto, la sucesión converge a 2.
Propiedades de las sucesiones convergentes
Las sucesiones convergentes tienen una serie de propiedades que veremos a continuación.
1) Unicidad del límite
Una sucesión convergente no puede tener más de un límite. Formalmente, si \(\lim_{n \to \infty} a_n=L\) y \(\lim_{n \to \infty} a_n=M,\) entonces necesariamente \(L=M.\) Esto significa que el límite, si existe, es único.
Demostración
Sea \(\epsilon>0.\) Como \(\lim_{n\to\infty} a_n=L,\) existe \(N_1\) tal que, para todo \(n>N_1,\)
\(|a_n-L|<\dfrac{\epsilon}{2}\)
También, dado que \(\lim_{n\to\infty} a_n=M,\) existe \(N_2\) tal que, para todo \(n>N_2,\)
\(|a_n-M|<\dfrac{\epsilon}{2}\)
Tomando \(N=\max\{N_1,N_2\}.\) Para todo \(n>N,\) por la desigualdad triangular,
\(|L-M|=|L-a_n+a_n-M|≤|L-a_n|+|a_n-M|<\dfrac{\epsilon}{2}+\dfrac{\epsilon}{2}=\epsilon\)
Como esto vale para todo \(\epsilon>0,\) \(|L-M|\) es menor que cualquier número positivo, la única posibilidad es que \(|L-M|=0,\) luego \(L=M.\)
Si los términos \(a_n\) están simultáneamente "arbitrariamente cerca" de L y de M, entonces L y M no pueden estar separados por una distancia positiva; la única posibilidad es que coincidan.
2) Toda sucesión convergente está acotada
Si una sucesión converge, sus términos no pueden crecer sin límite ni disminuir indefinidamente. En otras palabras, existe un número M > 0 tal que \(|a_n| ≤ M\) para todo n. Por lo tanto, la convergencia implica acotación, aunque la acotación por sí sola no garantiza convergencia.
Demostración
Sea \((a_n)\) una sucesión convergente con \(\lim_{n \to \infty} a_n=L.\) Queremos demostrar que \(\{a_n\}\) está acotada.
Por la definición de convergencia, dado cualquier \(\epsilon>0,\) existe \(N \in \mathbb{N}\) tal que para todo \(n > N,\) \(|a_n-L|<\epsilon.\)
Aplicando la desigualdad triangular:
\(|a_n|=|a_n-L+L| \leq |a_n-L|+|L|<\epsilon+|L|\)
Por lo tanto, para \(n > N,\) \(|a_n|<\epsilon+|L|.\) Hemos encontrado que para todos los términos mayores o iguales a N existe una cota para la sucesión.
Encontraremos una cota para el término N y los anteriores a él: los términos \(a_1, a_2, \dots, a_{N}\) son finitos. Definiremos como M’ al mayor de todos estos términos:
\(M'=\max\{|a_1|, |a_2|, \dots, |a_{N-1}|\}\)
Entonces, para \(n≤N,\)
\(|a_n| \leq M'\)
Es decir, el término N y todos los anteriores también están acotados.
Definimos una cota global tomando al máximo entre las dos cotas halladas:
\(M=\max\{M', \epsilon+|L|\}\)
Así, para todo \(n \in \mathbb{N},\) se cumple que \(|a_n| \leq M,\) como se quería demostrar.
3) Las subsucesiones de una sucesión convergente también convergen.
Si una sucesión \((a_n)\) converge a \(L,\) cualquier subsucesión \((a_{n_k})\) también converge al mismo valor \(L.\) Esto se debe a que extraer términos sin alterar el comportamiento a infinito no cambia el límite.
Demostración
Supongamos que la sucesión \((a_n)\) converge a \(L,\) es decir, para todo \(\varepsilon>0\) existe un número natural \(N\) tal que, para todo \(n \ge N,\) se cumple \(|a_n-L|<\varepsilon.\)
Consideremos ahora una subsucesión \((a_{n_k})\) de \((a_n),\) donde \(n_1<n_2<n_3<\cdots\) es una sucesión estrictamente creciente de índices. Como \(n_k \to \infty,\) llegará un momento en el que todos los índices \(n_k\) serán mayores o iguales que \(N.\) En otras palabras, existe un \(K\) tal que para todo \(k \ge K\) se cumple \(n_k \ge N.\)
Para esos valores de \(k,\) se tiene \(|a_{n_k}-L|<\varepsilon,\) ya que \(a_{n_k}\) es simplemente uno de los términos de la sucesión original con índice mayor o igual que \(N.\) Esto vale para cualquier \(\varepsilon>0,\) lo que implica que
\(\lim_{k \to \infty} a_{n_k}=L\)
Intuitivamente, una subsucesión no "escapa" del comportamiento final de la sucesión original: si los términos de \((a_n)\) están todos dentro de un margen \(\varepsilon\) de \(L\) a partir de cierto punto, entonces cualquier selección infinita de esos términos también estará dentro de ese margen y, por tanto, se acercará al mismo límite.
4) Toda sucesión constante es convergente.
Si \(a_n=c\) para todo \(n,\) entonces:
\(\lim_{n \to \infty} c=c\)
El límite es simplemente el valor de la constante.
Demostración
Supongamos que \((a_n)\) es una sucesión constante, es decir, existe un número real \(c\) tal que \(a_n=c\) para todo \(n \in \mathbb{N}.\) Queremos mostrar que esta sucesión es convergente y determinar su límite.
Tomemos un \(\varepsilon>0\) cualquiera. Para cualquier índice \(n,\) tenemos
\(|a_n-c|=|c-c|=0\)
Observamos que \(0<\varepsilon\) para cualquier \(\varepsilon>0,\) por lo que se cumple la condición de convergencia: para todo \(\varepsilon>0,\) existen índices \(n\) (de hecho, todos los índices) para los cuales \(|a_n-c|<\varepsilon.\)
Esto demuestra que la sucesión \((a_n)\) converge y que su límite es precisamente \(c:\)
\(\lim_{n \to \infty} a_n=c\)
5) Operaciones con sucesiones convergentes
La suma, diferencia, producto, y cociente (siempre que el denominador no tienda a 0) de sucesiones convergentes también son convergentes, con límites correspondientes a las operaciones en sus límites.
Si \(\lim_{n \to \infty} a_n=A\) y \(\lim_{n \to \infty} b_n=B,\) entonces:
- Suma y diferencia: \(\lim_{n \to \infty} (a_n±b_n)=\lim_{n \to \infty} a_n±\lim_{n \to \infty} b_n=A±B\)
- Producto: \(\lim_{n \to \infty} (a_n \cdot b_n)=\left(\lim_{n \to \infty} a_n\right) \cdot \left(\lim_{n \to \infty} b_n\right)=A \cdot B\)
- Cociente: \(\lim_{n \to \infty} \dfrac{a_n}{b_n}=\dfrac{\lim_{n \to \infty} a_n}{\lim_{n \to \infty} b_n}=\dfrac{A}{B} \quad \text{si } B \ne 0\)
6) Signo de los términos en el límite
Si una sucesión tiene límite positivo, existe un índice a partir del cual todos los términos de la sucesión son positivos. Simbólicamente, si \(\lim_{n \to \infty} a_n=L>0,\) entonces existe un número natural \(N\) tal que para todo \(n>N\) se cumple que \(a_n>0.\)
De forma análoga, si una sucesión tiene límite negativo, existe un índice a partir del cual todos los términos son negativos. En notación formal, si \(\lim_{n \to \infty} a_n=L<0,\) existe \(N\) tal que para todo \(n>N:\) \(a_n<0.\)
7) Multiplicación por una constante
Si cada término de una sucesión convergente se multiplica por una constante k, entonces el límite es igual a k multiplicado por el límite original.
Si \(\lim_{n \to \infty} a_n=A\) y \(c\) es una constante real, entonces:
\(\lim_{n \to \infty} (c \cdot a_n)=c \cdot \lim_{n \to \infty} a_n=c \cdot A\)
8) Límite de términos consecutivos
En una sucesión convergente, el límite del término siguiente es el mismo que el del término actual:
\(\lim_{n \to \infty} a_{n+1}=\lim_{n \to \infty} a_n\)
Esto se debe a que desplazar el índice en una cantidad finita no altera el comportamiento de la sucesión.
Demostración
Supongamos que \((a_n)\) es una sucesión convergente con límite \(L,\) es decir:
\(\lim_{n \to \infty} a_n=L\)
Por definición, esto significa que para todo \(\varepsilon>0\) existe un número natural \(N\) tal que para todo \(n>N,\) se cumple:
\(|a_n-L|<\varepsilon\)
Ahora consideremos la sucesión desplazada \((a_{n+1}).\) Para cualquier índice \(n>N,\) tenemos que \(n+1>N\) a partir de cierto índice \(N'.\) Por lo tanto:
\(|a_{n+1}-L|<\varepsilon \quad \text{para todo } n>N'\)
Esto demuestra que la sucesión \((a_{n+1})\) también se aproxima al mismo límite \(L:\)
\(\lim_{n \to \infty} a_{n+1}=L=\lim_{n \to \infty} a_n\)
Bibliografía
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

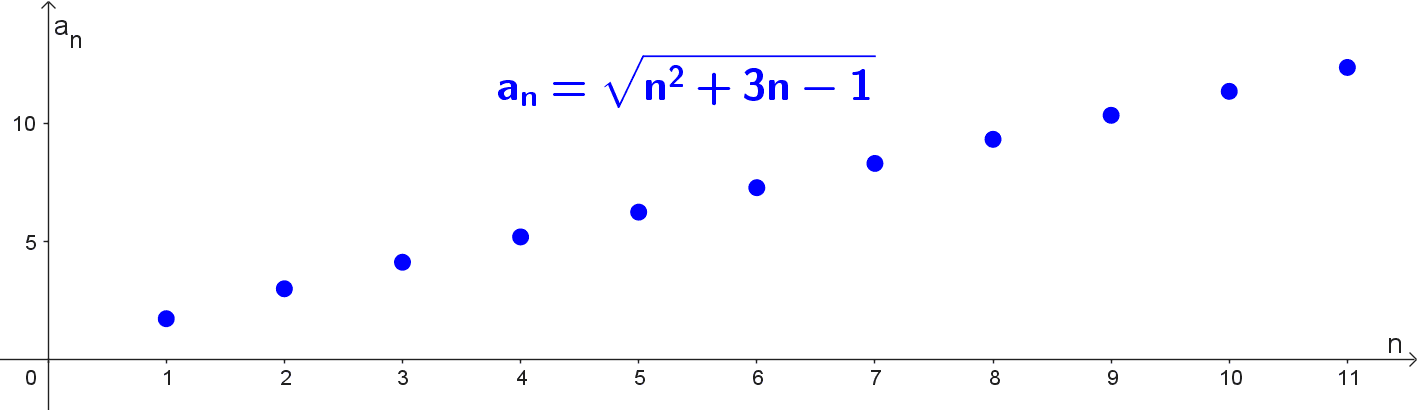
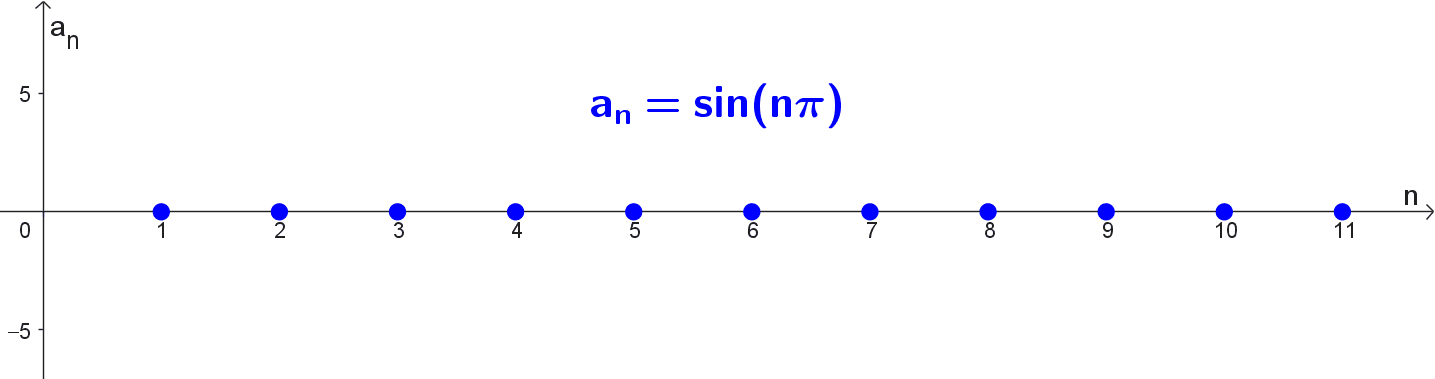
Otros artículos que pueden interesarte