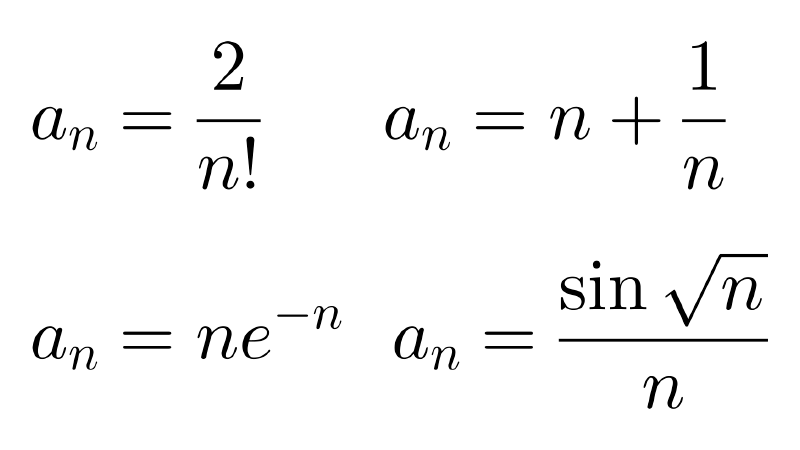
Sucesión divergente
Una sucesión divergente es aquella que no tiene límite finito, es decir, sus términos no se acercan a un valor fijo a medida que avanzamos en la sucesión. Puede ocurrir que sus términos crecen sin límite (diverge a ∞), se hacen cada vez más negativos (diverge a -∞), o los términos oscilan entre distintos valores sin acercarse a uno fijo (diverge por oscilación).
En contraste, una sucesión convergente es aquella que sí se acerca a un valor numérico fijo a medida que avanzamos en la sucesión, es decir, tiene límite finito. Algunos autores distinguen entre sucesión "no convergente" y "divergente", pero en este artículo adoptamos la convención de que toda sucesión no convergente es divergente.
Algunos ejemplos son:
- (2n) = (2, 4, 6, 8, 10, …) es una sucesión que diverge a ∞ porque sus términos se hacen cada vez más grandes.
- La sucesión (-n) = (-1, -2, -3, -4, -5, …) diverge a menos infinito porque los términos se hacen cada vez más negativos.
- La secuencia ( (-1)n ) = (-1, 1, -1, 1, -1, …) diverge por oscilación porque los términos "saltan" entre -1 y 1.
Índice
Tipos de divergencia
Existen tres tipos de divergencia: dos en los que el límite de la sucesión es infinito (positivo o negativo) y uno en el que no existe ningún límite, ni finito ni infinito. Más adelante abordaremos cada caso de manera detallada.
De forma rigurosa, una sucesión puede definirse como divergente negando la definición de convergencia:
Una sucesión (an) es divergente si y solo si, para todo número real L, existe un ε > 0 tal que para todo número natural N, se puede encontrar un n ≥ N con |an − L| ≥ ε.
La definición dice que no importa qué valor real L se tome como candidato a límite, siempre quedarán infinitos términos de la sucesión que se alejan de L más de una cierta cantidad fija (ε). Es decir, nunca se logra que los términos se acerquen y permanezcan arbitrariamente cerca de un mismo valor real, como sí ocurre en una sucesión convergente.
Divergencia positiva
Se dice que una sucesión diverge a infinito positivo cuando sus términos crecen sin límite, es decir, cuando a medida que avanza la sucesión los valores se hacen cada vez más grandes. De manera intuitiva, esto significa que los términos siguen aumentando sin detenerse y no hay un número real que pueda servir como "tope".
La definición formal establece que una sucesión (an) diverge a infinito si para todo número positivo M, existe un número natural N tal que si n ≥ N, entonces an > M. Esto quiere decir que, para cualquier número M > 0 que se elija, no importa lo grande que sea, siempre existirá un índice N tal que todos los términos posteriores de la sucesión serán mayores que M. Simbolizamos esta situación de la siguiente forma:
\(\lim_{n \to ∞} a_n=+∞\)
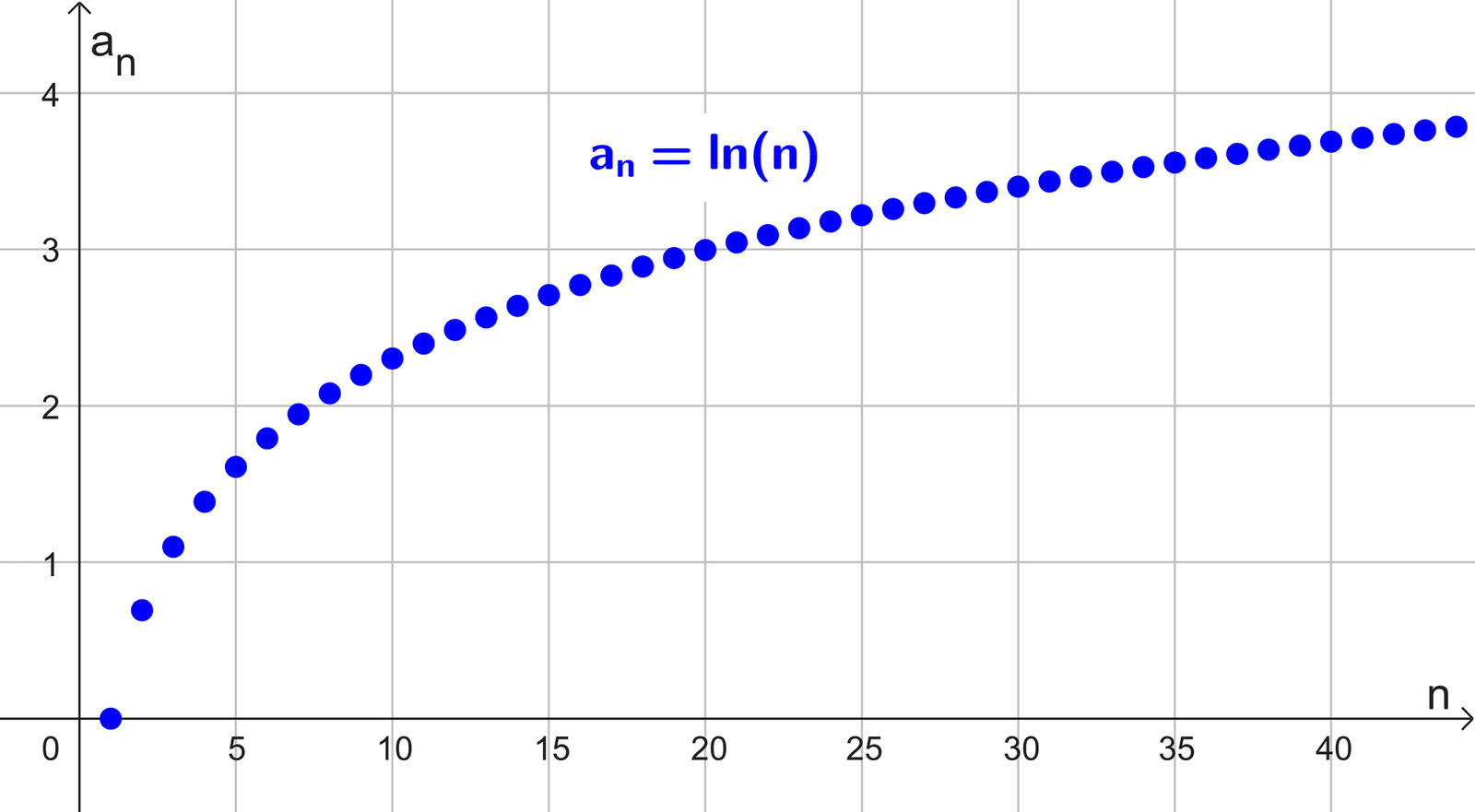
Si se representa gráficamente, se observa que los puntos de la sucesión se elevan cada vez más, avanzando hacia el infinito positivo (es decir, hacia arriba en el eje vertical).
Algunos ejemplos de sucesiones que divergen a infinito positivo son:
- (n) = (1, 2, 3, 4, 5, …), la sucesión de números naturales.
- (2n - 1) = (1, 3, 5, 7, 9, 11, 13, …), la sucesión de los números impares positivos.
- (n2) = (1, 4, 9, 16, 25, …), la sucesión de los cuadrados de los números naturales.
- (2n) = (2, 4, 8, 16, 32, …), una sucesión exponencial de base positiva mayor que 1.
- ( an = ln(n) ), aunque el logaritmo crezca muy lentamente, la sucesión diverge porque no está acotada superiormente.
Divergencia negativa
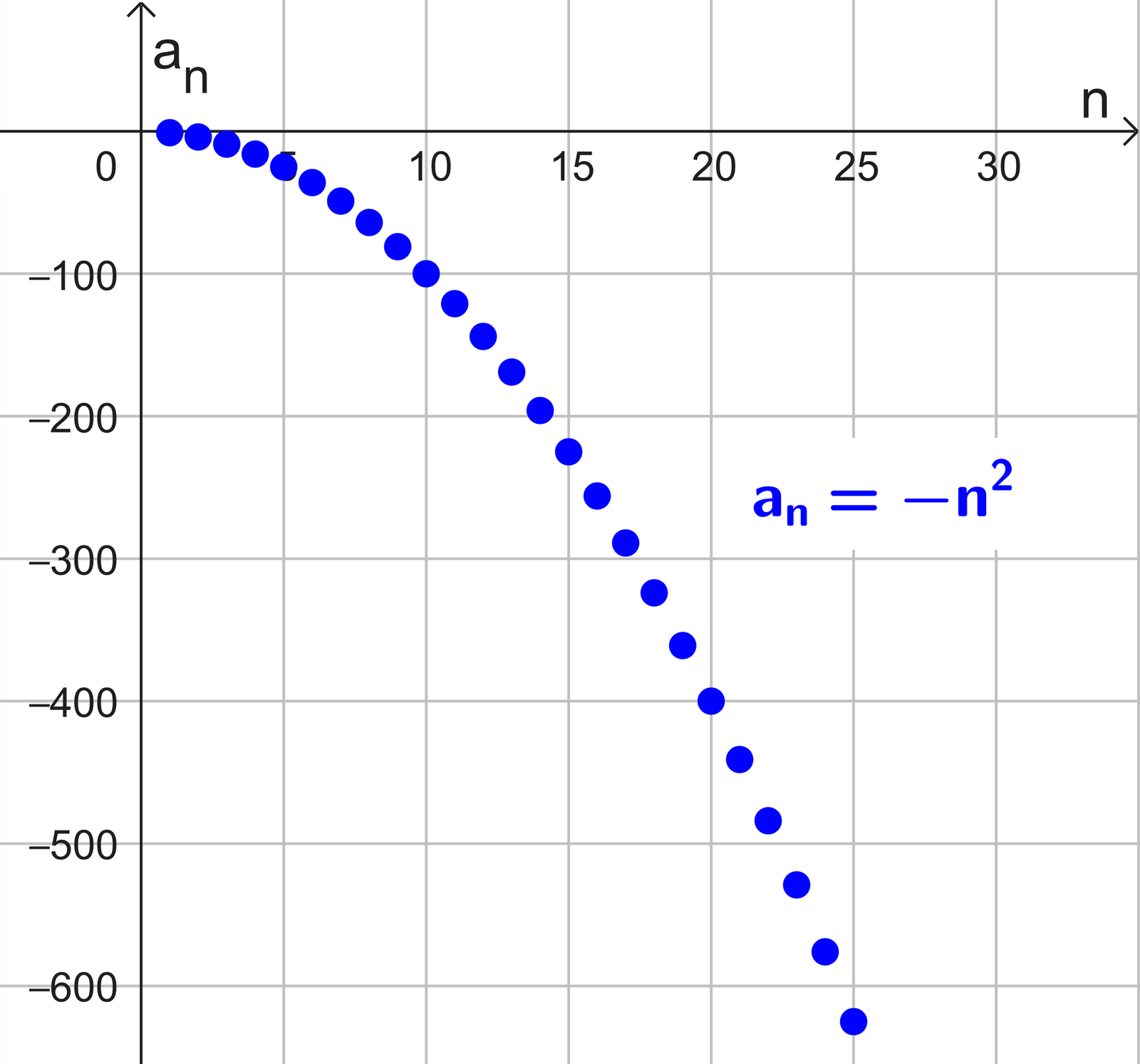
Una sucesión diverge a infinito negativo cuando sus términos decrecen sin límite, es decir, cuando a medida que avanza la sucesión los valores se hacen cada vez más pequeños en el sentido de volverse más negativos. De manera intuitiva, esto significa que los términos de la sucesión descienden indefinidamente y no existe un número real que pueda servir como "piso".
La definición formal establece que una sucesión (an) diverge a infinito negativo si para todo número negativo M, existe un número natural N tal que si n ≥ N, entonces an < M. Esto quiere decir que, para cualquier número M < 0 que se elija, siempre existirá un índice N tal que todos los términos posteriores de la sucesión serán menores que M. Simbolizamos esta situación de la siguiente forma:
\(\lim_{n \to ∞} a_n=-∞\)
Gráficamente observamos que los puntos de la sucesión descienden cada vez más, avanzando hacia el infinito negativo (es decir, hacia abajo en el eje vertical).
Algunos ejemplos de sucesiones que divergen a infinito negativo son:
- (-n) = (-1, -2, -3, -4, -5, …), la sucesión de enteros negativos.
- (-n2) = (-1, -4, -9, -16, …), la sucesión de cuadrados negativos.
- (-2n) = (-2, -4, -6, -8, …), una sucesión de números pares negativos.
- (-3n) = (-2, -4, -8, -16, …), una sucesión exponencial negativa.
Nota: cuando escribimos \(\lim_{n \to ∞} a_n=+∞\) o \(\lim_{n \to ∞} a_n=-∞,\) no debe interpretarse que el límite existe, ya que el infinito no es un número real. Lo que estas expresiones indican es precisamente la razón por la cual el límite no existe: la sucesión crece o decrece sin límite. Por este motivo, conviene evitar expresiones como "la sucesión converge a infinito", ya que pueden generar confusión respecto al concepto de convergencia, el cual se reserva solo para límites finitos.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Divergencia por oscilación
Una sucesión diverge por oscilación cuando no tiene límite finito ni infinito. Esto significa que sus términos no se acercan a un único número real fijo, pero tampoco crecen o decrecen de manera constante hacia el infinito o menos infinito. En su lugar, los valores de la sucesión "saltan" o alternan entre diferentes valores.
Esta oscilación puede presentarse de dos formas principales: con los términos alternando entre un conjunto finito de valores (oscilación finita) o con los términos creciendo en valor absoluto pero alternando su signo (oscilación infinita).
Algunos ejemplos de sucesiones que divergen por oscilación son:
- ( (-1)n ) = (-1, 1, -1, 1, -1, …), los valores de esta sucesión saltan entre -1 y 1, diverge por oscilación finita.
- (0, 1, 2, 0, 1, 2, …), en esta sucesión los términos alternan entre tres valores que se repiten constantemente, la oscilación es finita.
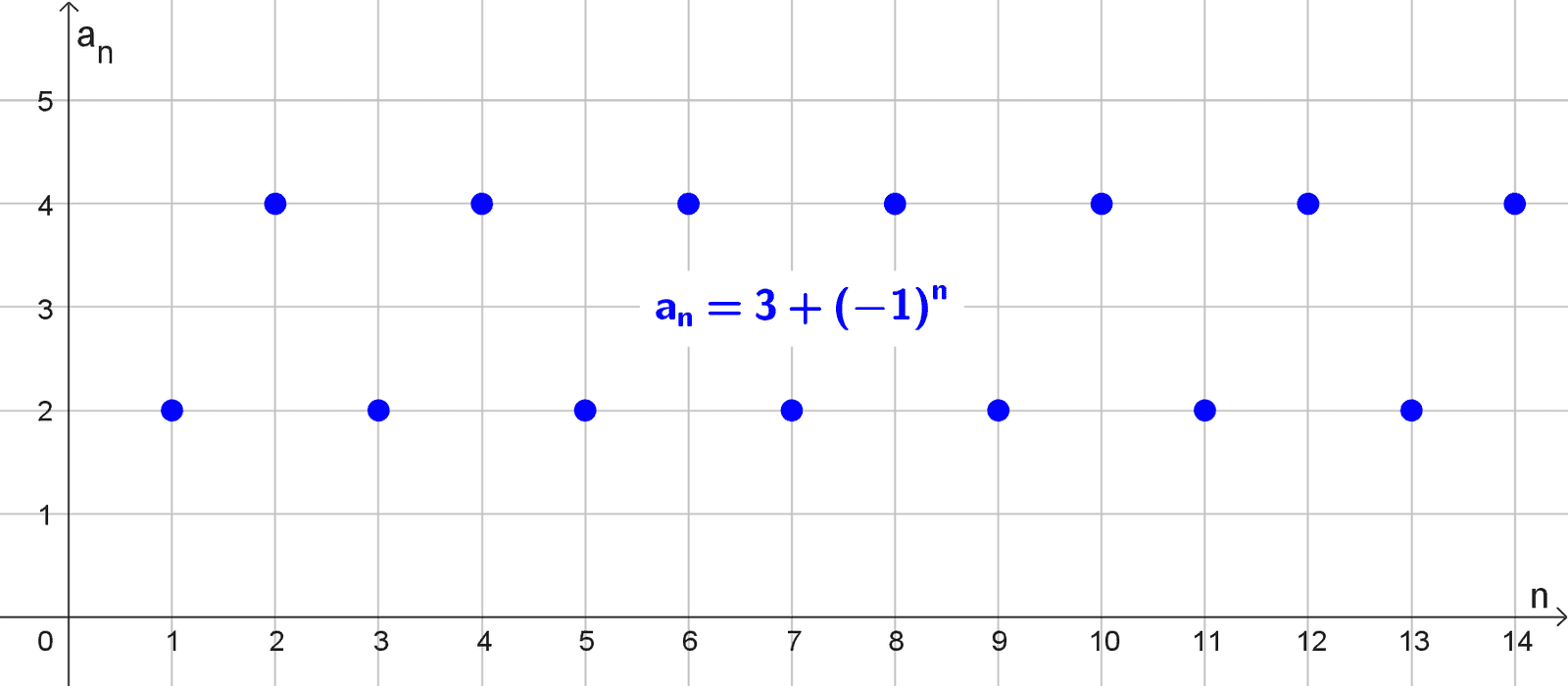
- ( 3 + (-1)n ) = (4, 2, 4, 2, 4, 2, …) es una sucesión oscilante entre los valores 4 y 2.
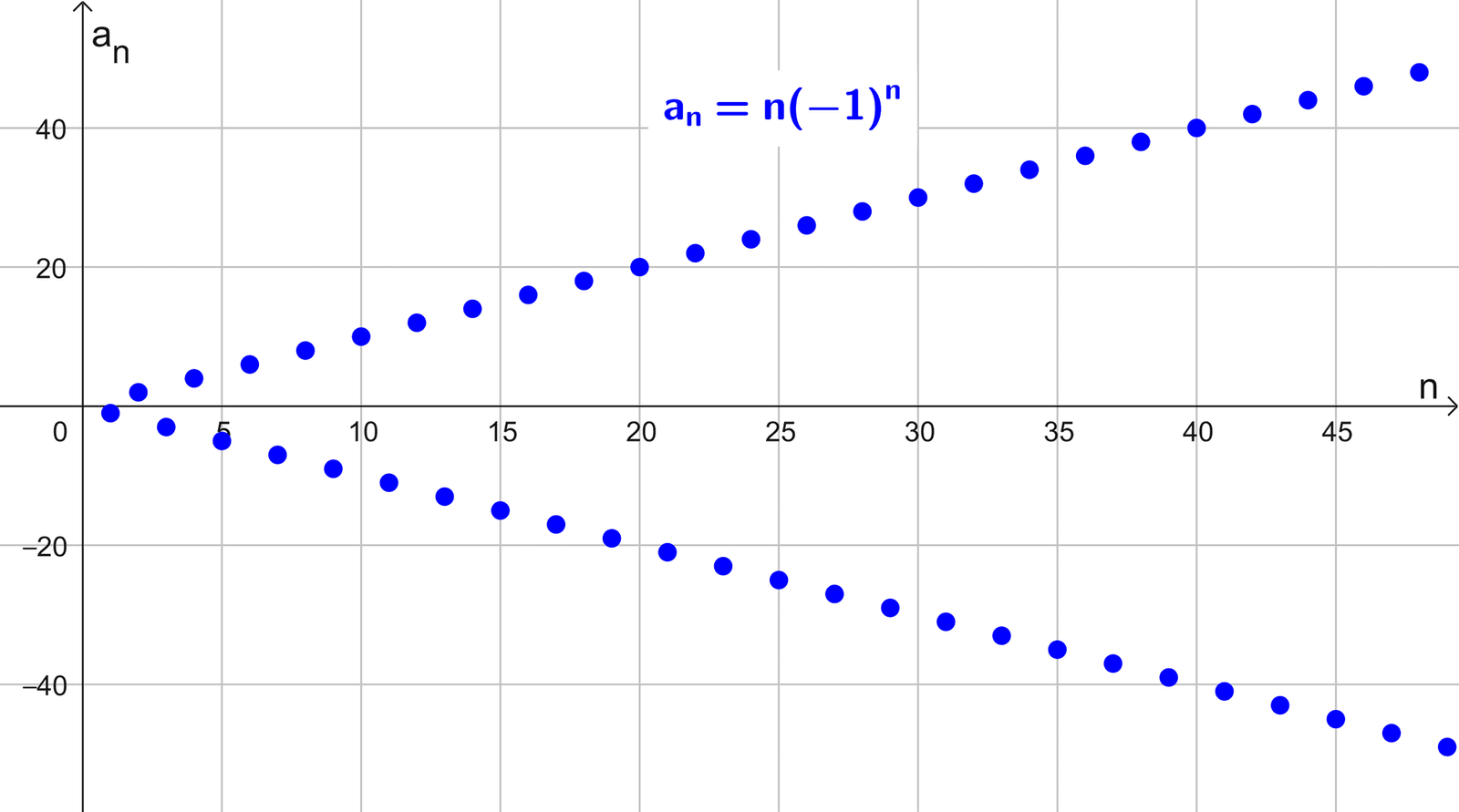
- ( n(-1)n ) = (-1, 2, -3, 4, -5, 6, -7, …) los términos de esta secuencia crecen en valor absoluto pero alternan de signo en cada paso, por lo que no diverge a infinito ni menos infinito, sino que diverge por oscilación infinita.
- Las sucesiones ( sin(n) ) y ( cos (n) ) oscilan en el intervalo [-1, 1].
Cómo saber si una sucesión diverge
Para determinar si una sucesión diverge, podemos analizar distintas propiedades de la misma. Entre los criterios más comunes se encuentran el estudio del límite, el análisis de monotonía y acotamiento, o la observación del comportamiento de sus subsucesiones.
Análisis del límite
El primer paso natural para determinar si una sucesión diverge es estudiar el límite de su término general cuando n tiende a infinito. Si el límite existe y es un número real, la sucesión es convergente; en cambio, si el límite resulta ser \(+∞\) o \(-∞,\) la sucesión diverge hacia infinito positivo o negativo, respectivamente. Finalmente, si el límite no existe y no es un caso de infinito, la sucesión es oscilante.
En caso de aparecer indeterminaciones, podemos aplicar las técnicas habituales para resolverlas, como dividir numerador y denominador por la variable elevada a la mayor potencia presente, aplicar la regla de L’Hospital, etc.
Ejemplo 1
Analizar la convergencia de la sucesión con término general \(a_n=\dfrac{2n}{n+1}.\)
Solución
Calculamos el siguiente límite:
\(\lim_{n \to ∞} \dfrac{2n}{n+1}\)
Como se presenta una indeterminación ∞/∞, dividimos numerador y denominador entre n:
\(\lim_{n \to ∞} \dfrac{2}{1+\frac{1}{n}}=2\)
En este caso, se trata de una sucesión convergente con límite 2.
Ejemplo 2
Determinar si la sucesión con término enésimo \(b_n=\dfrac{n^2}{n+1}\) converge o diverge.
Solución
Calculamos el siguiente límite:
\(\lim_{n \to ∞} \dfrac{n^2}{n+1}\)
Como se presenta una indeterminación, dividimos numerador y denominador entre \(n^2:\)
\(\lim_{n \to ∞} \dfrac{1}{\dfrac{1}{n}+\dfrac{1}{n^2}}=+∞\)
En este caso, la sucesión diverge a infinito.
Ejemplo 3
Estudie la convergencia de la sucesión definida por \(c_n=\dfrac{-3n}{\sqrt{n+1}}.\)
Solución
Debemos calcular el siguiente límite:
\(\lim_{n \to ∞} \dfrac{-3n}{\sqrt{n+1}}\)
De nuevo hay una indeterminación, dividimos numerador y denominador entre \(n:\)
\(\lim_{n \to ∞} \dfrac{-3}{\sqrt{\dfrac{1}{n}+\dfrac{1}{n^2}}}=-∞\)
En este caso, la sucesión diverge a menos infinito.
Sucesión de valores absolutos
En algunos casos, el cálculo directo del límite de una sucesión no es posible o no proporciona un resultado concluyente. Esto ocurre frecuentemente con sucesiones oscilantes, donde un factor como (-1)n hace que los términos alternen su signo.
Para demostrar la divergencia en estos casos, podemos recurrir a un método alternativo: analizar el comportamiento de la sucesión de los valores absolutos de sus términos. Un teorema muy útil establece que si la sucesión de los valores absolutos, |an|, diverge positivamente (es decir, su límite es \(+∞\)), entonces la sucesión original an también es divergente. La razón es que los términos de an crecen en magnitud sin cota, independientemente de su signo.
Ejemplo 1
Analizar si la sucesión con fórmula general \(a_n=n \cdot (-1)^n\) es divergente.
Solución
Consideremos la sucesión de los valores absolutos de sus términos, que es \(|a_n|=|n \cdot (-1)^n|=n.\) Ahora, calculamos el límite de esta nueva sucesión:
\(\lim_{n \to ∞} |a_n|=\lim_{n \to ∞} n=+∞\)
Dado que la sucesión de los valores absolutos diverge positivamente, podemos concluir que la sucesión original \(a_n=n \cdot (-1)^n\) también es divergente.
Ejemplo 2
Determinar el carácter de la sucesión definida por \(b_n=(-2)^n.\)
Solución
Comenzamos construyendo la sucesión de los valores absolutos: \(|b_n|=|(-2)^n|=2^n.\) Procedemos a hallar el límite de esta sucesión:
\(\lim_{n \to ∞} |b_n|=\lim_{n \to ∞} 2^n=+∞\)
El resultado confirma que la sucesión de los valores absolutos diverge. Por lo tanto, la sucesión original \(b_n=(-2)^n\) es divergente.
Ejemplo 3
Estudiar la convergencia de la sucesión \(c_n=(-1)^n \cdot \ln(n).\)
Solución
Para aplicar el criterio, examinamos la sucesión de valores absolutos: \(|c_n|=|(-1)^n \cdot \ln(n)|=\ln(n).\) Calculamos su límite:
\(\lim_{n \to ∞} |c_n|=\lim_{n \to ∞} \ln(n)=+∞\)
Como el límite es infinito, la sucesión de valores absolutos diverge. En consecuencia, la sucesión original \(c_n\) es divergente. La función logaritmo, aunque crece lentamente, tiende a infinito, y esto, combinado con la oscilación del signo, resulta en una sucesión que no se estabiliza alrededor de ningún punto.
Nota: un teorema establece que si la sucesión de valores absolutos |an| converge a cero, entonces la sucesión original an también converge a cero. Sin embargo, si |an| converge a un número L ≠ 0, no podemos garantizar que an converja. Un contraejemplo clásico es la sucesión oscilante an = (-1)n, donde |an| = 1 converge a 1, pero la sucesión original an no converge porque oscila entre -1 y 1.
Estudio de las subsucesiones
Una subsucesión se forma seleccionando términos de la sucesión original en un orden creciente de índices; por ejemplo, si tenemos la sucesión an, una de sus subsucesiones podría ser a2n, que toma todos los términos de índice par.
Una propiedad fundamental de las sucesiones convergentes es que si una sucesión converge a un límite L, entonces todas sus subsucesiones también deben converger al mismo valor L. Este hecho nos proporciona un criterio muy útil para detectar divergencia: si podemos encontrar al menos dos subsucesiones de an que converjan a límites diferentes, entonces la sucesión original an no puede ser convergente y, por lo tanto, es divergente.
Ejemplo 1
Demostrar mediante subsucesiones que la sucesión \(a_n=(-1)^n\) no es convergente.
Solución
Consideremos dos subsucesiones naturales de \(a_n.\) Primero, tomemos la subsucesión formada por todos los términos de índice par: \(a_{2n}=(-1)^{2n}=1.\) El límite de esta subsucesión es:
\(\lim_{n \to ∞} a_{2n}=\lim_{n \to ∞} 1=1\)
Ahora, consideremos la subsucesión formada por los términos de índice impar: \(a_{2n-1}=(-1)^{2n-1}=-1.\) El límite de esta subsucesión es:
\(\lim_{n \to ∞} a_{2n-1}=\lim_{n \to ∞} (-1)=-1\)
Hemos encontrado dos subsucesiones que convergen a límites distintos: 1 y -1. Según la propiedad mencionada, si la sucesión original fuera convergente, todas sus subsucesiones deberían tender al mismo límite. Como este no es el caso, concluimos que la sucesión \(a_n=(-1)^n\) es divergente.
Ejemplo 2
Analizar el comportamiento de la sucesión \(b_n=\cos(n\pi).\)
Solución
Observamos que \(\cos(n\pi)\) alterna su valor dependiendo de si \(n\) es par o impar. Para aplicar el criterio de las subsucesiones, elegimos dos específicas. La primera es la subsucesión de términos pares: \(b_{2n}=\cos(2n\pi)=\cos(0)=1.\) Calculamos su límite:
\(\lim_{n \to ∞} b_{2n}=\lim_{n \to ∞} 1=1\)
La segunda subsucesión es la de términos impares: \(b_{2n-1}=\cos((2n-1)\pi)=\cos(\pi)=-1.\) Su límite es:
\(\lim_{n \to ∞} b_{2n-1}=\lim_{n \to ∞} (-1)=-1\)
Estas dos subsucesiones convergen a valores diferentes, 1 y -1. Por lo tanto, la sucesión original \(b_n=\cos(n\pi)\) no puede ser convergente y debemos clasificarla como divergente.
Análisis de monotonía y acotamiento
El estudio de la monotonía y la acotación de una sucesión es muy útil para determinar su convergencia o divergencia. Una sucesión es monótona si sus términos siempre aumentan (creciente) o siempre disminuyen (decreciente). Por otro lado, una sucesión está acotada si existe un número real que limita la magnitud de todos sus términos.
Un teorema fundamental del análisis establece que toda sucesión monótona y acotada es convergente. Este resultado es muy potente, pero su contrarrecíproco también nos ofrece un criterio valioso para la divergencia: si una sucesión no está acotada, entonces necesariamente diverge.
La razón es simple: para que una sucesión converja a un límite finito, sus términos deben acercarse cada vez más a ese valor, lo que impide que crezcan o decrezcan sin control. Por lo tanto, si podemos demostrar que una sucesión no está acotada (ya sea superior o inferiormente), podemos concluir inmediatamente que es divergente. Una sucesión creciente y no acotada diverge a infinito; análogamente, una sucesión decreciente y no acotada diverge a menos infinito.
Ejemplo
Demostrar que la sucesión definida por \(a_n=2^n\) es divergente analizando su acotación.
Solución
Estudiamos si la sucesión \(a_n=2^n\) está acotada. Supongamos, por contradicción, que sí lo está. Esto significaría que existe un número real \(M>0\) tal que \(|2^n| ≤ M\) para todo número natural \(n.\) Sin embargo, la función exponencial de base 2 crece de manera ilimitada. Para verlo, tomemos logaritmos: la desigualdad \(2^n ≤ M\) implica \(n ≤ \log_2(M).\) Pero \(n\) puede ser cualquier número natural, por lo que siempre podemos tomar un \(n\) mayor que \(\log_2(M),\) rompiendo la desigualdad. Por ejemplo, si elegimos \(n=\lfloor \log_2(M) \rfloor+1,\) obtenemos \(2^n>M.\)
Esta contradicción prueba que no existe tal cota \(M.\) La sucesión \(a_n=2^n\) no está acotada superiormente. En consecuencia, y dado que es creciente y sus términos se vuelven arbitrariamente grandes, podemos afirmar que diverge positivamente:
\(\lim_{n \to ∞} 2^n=+∞\)
Nota: una sucesión no acotada siempre diverge, sin embargo, el hecho de que una sucesión esté acotada no garantiza su convergencia. La sucesión (-1)n es el contraejemplo clásico: está acotada entre -1 y 1, pero ya hemos visto que es divergente porque oscila entre esos mismos valores. La acotación es una condición necesaria para la convergencia, pero no es suficiente por sí sola.
Propiedades
Al operar con sucesiones divergentes, es importante comprender cómo interactúan entre sí y con otros tipos de sucesiones. A continuación, se detallan las propiedades para la suma, resta, multiplicación y división.
Suma y resta
- Si dos sucesiones divergen, ambas hacia \(+∞\) o ambas hacia \(-∞,\) su suma también divergirá hacia \(+∞\) o \(-∞,\) respectivamente.
- Si una sucesión diverge hacia \(+∞\) y otra diverge hacia \(-∞,\) su suma o resta resulta en una indeterminación. El resultado final puede ser convergente, divergente a infinito, o divergente de otra forma, y se requiere un análisis específico.
- Si una sucesión diverge a \(+∞\) o a \(-∞\) y se suma o resta con una sucesión acotada, el resultado será la misma divergencia original.
Multiplicación
- El producto de dos sucesiones que divergen al infinito con el mismo signo (ambas a \(+∞\) o ambas a \(-∞\)) resulta en una sucesión que diverge hacia \(+∞.\)
- El producto de dos sucesiones que divergen al infinito con signos opuestos (una a \(+∞\) y la otra a \(-∞\)) resulta en una sucesión que diverge hacia \(-∞.\)
- Multiplicar una sucesión divergente por una constante no nula simplemente escala la divergencia. Si la constante es positiva, se mantiene el signo de la divergencia. Si la constante es negativa, se invierte el signo del infinito al que diverge.
- El producto de una sucesión divergente (a infinito) por una sucesión infinitesimal (que converge a cero) es una indeterminación. El resultado depende de la "velocidad" con la que una crece y la otra decrece.
División
- El cociente entre dos sucesiones que divergen a infinito (en cualquier combinación de signos) es una indeterminación. El resultado depende de cuál de las dos sucesiones crece a mayor velocidad.
- Dividir una sucesión divergente entre una sucesión acotada y no infinitesimal (su límite es un número \(k ≠ 0\)) resulta en una divergencia. El signo del infinito resultante sigue la regla de los signos de la división (\(+/+=+\), \(+/-=-,\) etc.).
- Dividir una sucesión acotada entre una sucesión divergente resulta en una sucesión infinitesimal, que converge a cero.
Resumen de propiedades
La siguiente tabla resume el comportamiento de las operaciones con sucesiones divergentes. Utilizamos la simbología \(∞\) para una sucesión que diverge positivamente, \(-∞\) para una que diverge negativamente, "acotada" para una sucesión acotada con límite \(k ≠ 0,\) "constante" para una constante no nula, y "0" para una sucesión infinitesimal (que tiende a 0).
| Operación | Resultado |
|---|---|
| \(∞ + ∞\) \(∞ ± \text{acotada}\) \(∞ × ∞\) \((-∞) × (-∞)\) \(∞ × \text{constante } >0\) \(-∞ × \text{constante } < 0\) \(∞ / \text{acotada }\) (k > 0) \(-∞ / \text{acotada }\) (k < 0) | \(∞\) |
| \(-∞ + (- ∞)\) \(-∞ ± \text{acotada}\) \(∞ × (-∞)\) \(-∞ × ∞\) \(∞ × \text{constante } < 0\) \(-∞ × \text{constante } > 0\) \(∞ / \text{acotada }\) (k < 0) \(-∞ / \text{acotada }\) (k > 0) | \(-∞\) |
| \(\text{acotada } / ∞ \) \(\text{acotada } / (-∞)\) | 0 |
| \(∞-∞\) \(∞ × 0\) \(∞/∞\) \(0/0\) \(1^∞\) \(0^0\) \(∞^0\) | Indeterminación |
Bibliografía
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

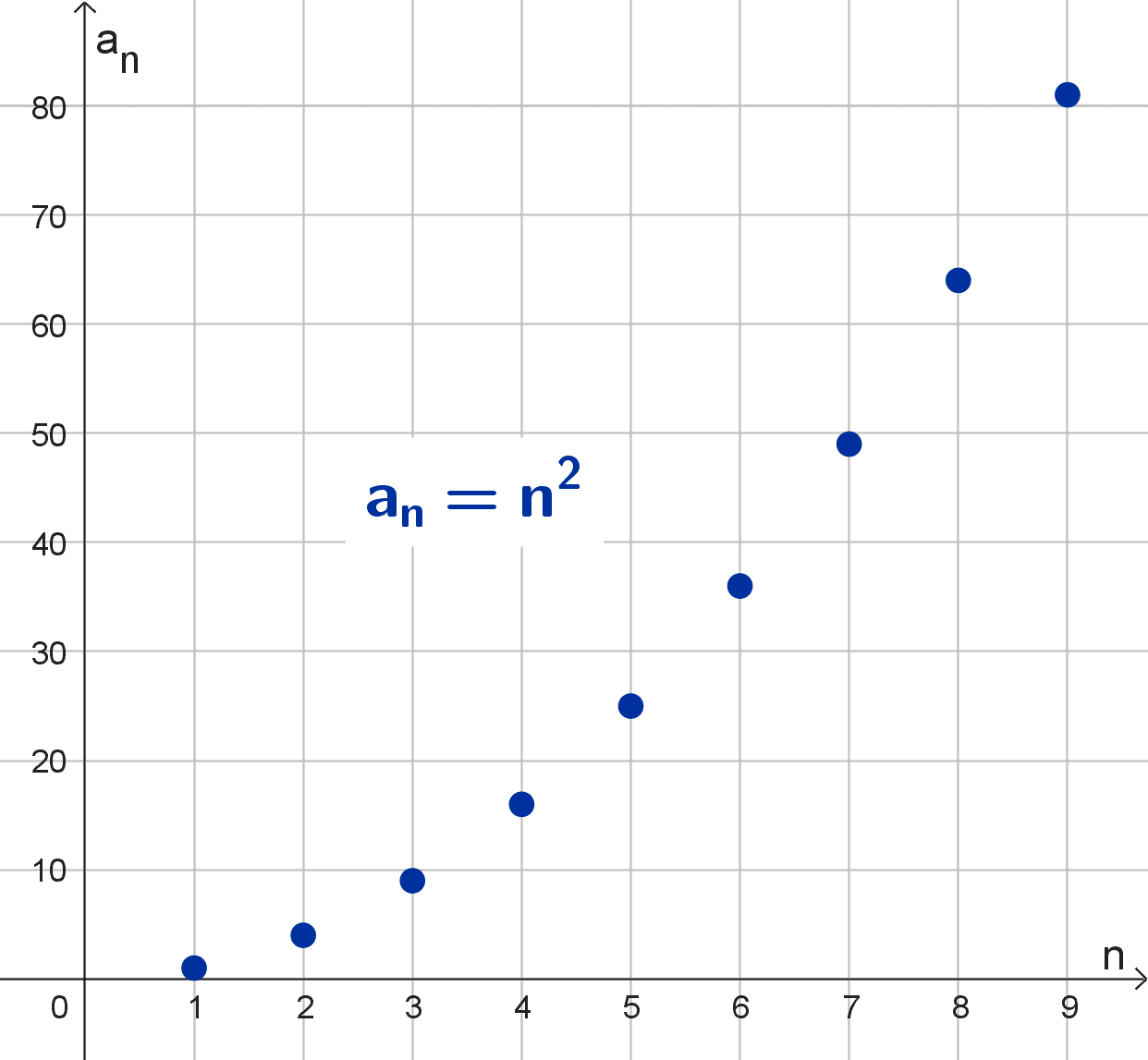
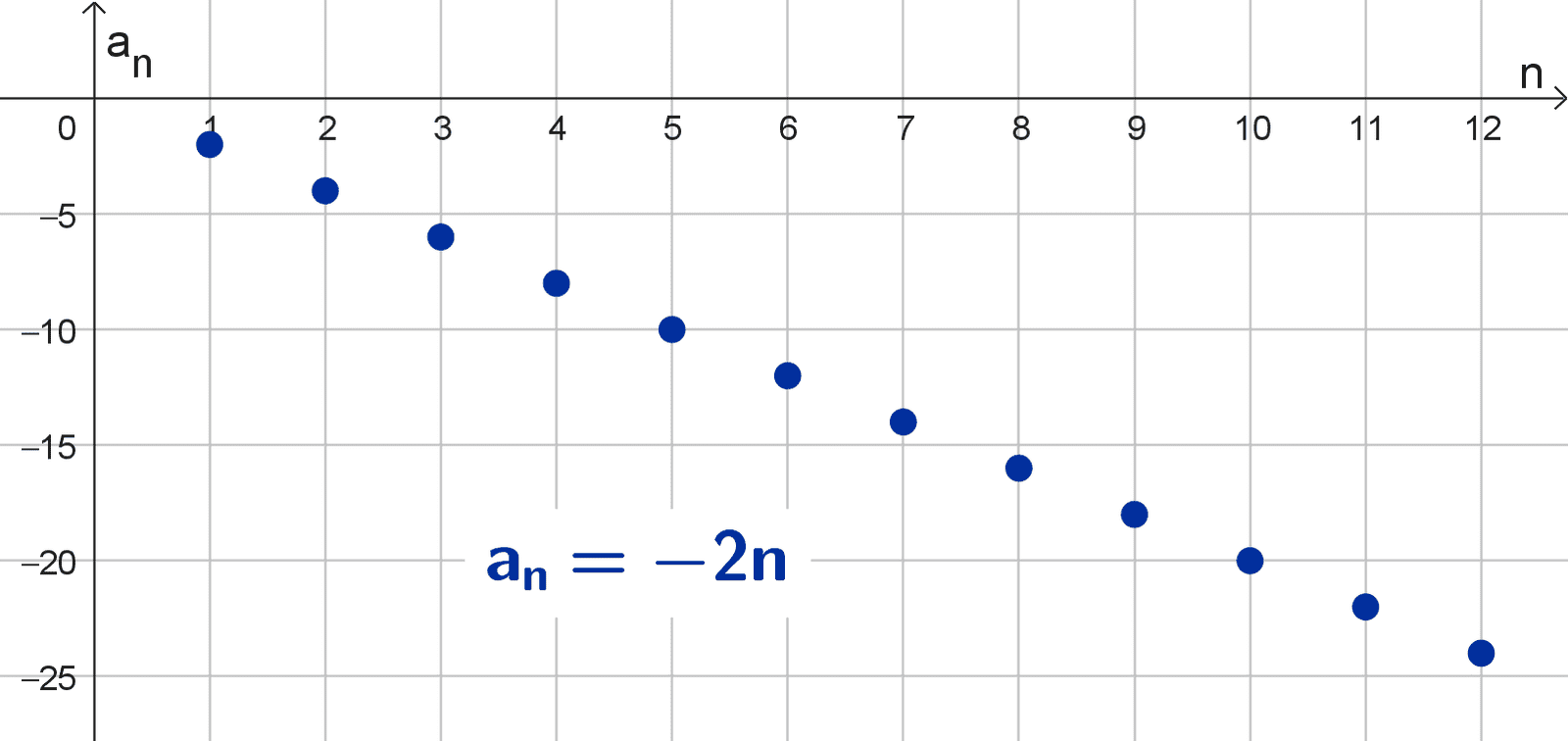
Otros artículos que pueden interesarte