Límite de una sucesión
El límite de una sucesión infinita es el valor al que se acercan los términos de la sucesión a medida que el número de términos tiende a infinito. Si este valor existe y es finito, la sucesión se dice que es convergente. Si el límite es infinito o no existe, la sucesión se considera divergente.
Ejemplos
- La sucesión infinita (1, 1/2, 1/3, 1/4, 1/5, 1/6, …) con término general \(a_n=\dfrac{1}{n}\) tiene límite cero 0 ya que sus términos se acercan cada vez más a ese valor cuando n tiende a infinito.
- La secuencia (1/2, 2/3, 3/4, 4/5, 5/6, 6/7, …) con término general \(b_n=\dfrac{n}{n+1}\) converge a 1 a medida que n se hace grande.
- La sucesión (2, 4, 6, 8, 10, 12, …) con término enésimo \(c_n=2n\) no tiene límite finito porque sus términos se hacen cada vez más grandes a medida que n crece. En este caso se dice que la sucesión diverge porque su límite es infinito.
- La sucesión (-1, 1, -1, 1, -1, 1, …) con fórmula general \(d_n=(-1)^n\) no se acerca a ningún valor a medida que n crece, sino que sus términos oscilan entre -1 y 1, por tanto, no existe límite finito y la sucesión diverge por oscilación.
Índice
Definición formal de límite finito
Una sucesión (an) converge a un número real L si ocurre que para todo ε > 0 existe un entero positivo N tal que |an - L| < ε siempre que n > N. El número L se llama límite de la sucesión y escribimos:
\(\lim_{n \to \infty} a_n = L\)
que se lee como "el límite cuando n tiende a infinito de la sucesión an es igual a L". También podemos simbolizarlo como \(a_n→L\) cuando \(n→∞,\) que se lee como "la sucesión an tiende a L cuando n tiende a infinito". Si an no converge, esto es, cuando su límite no existe, se dice que es una sucesión divergente. Si una sucesión converge, entonces su límite es único.
La definición simbólica puede llegar a confundir, pero su explicación es la siguiente: cuando decimos que una sucesión (an) tiene como límite un número L, lo que afirmamos es que, a medida que n crece mucho, los valores de la sucesión se acercan cada vez más a L, y podemos lograr que estén tan cerca como queramos.
Para expresar "tan cerca como queramos" de forma precisa, en matemáticas introducimos una letra griega: ε (épsilon). Este ε representa un margen de error, es decir, una distancia máxima permitida entre los términos de la sucesión y el valor L. Ese margen de error no es fijo: quien plantea el problema puede elegirlo tan grande o tan pequeño como quiera, lo habitual son números diminutos como 0,001.
El reto consiste en demostrar que, sin importar qué margen de error se elija, siempre podremos garantizar que los términos de la sucesión se mantengan dentro de esa distancia respecto a L, siempre y cuando estemos lo suficientemente lejos en la numeración de los términos. Aquí es donde aparece N: un número natural a partir del cual todos los términos cumplen con la condición de estar dentro del margen de error.
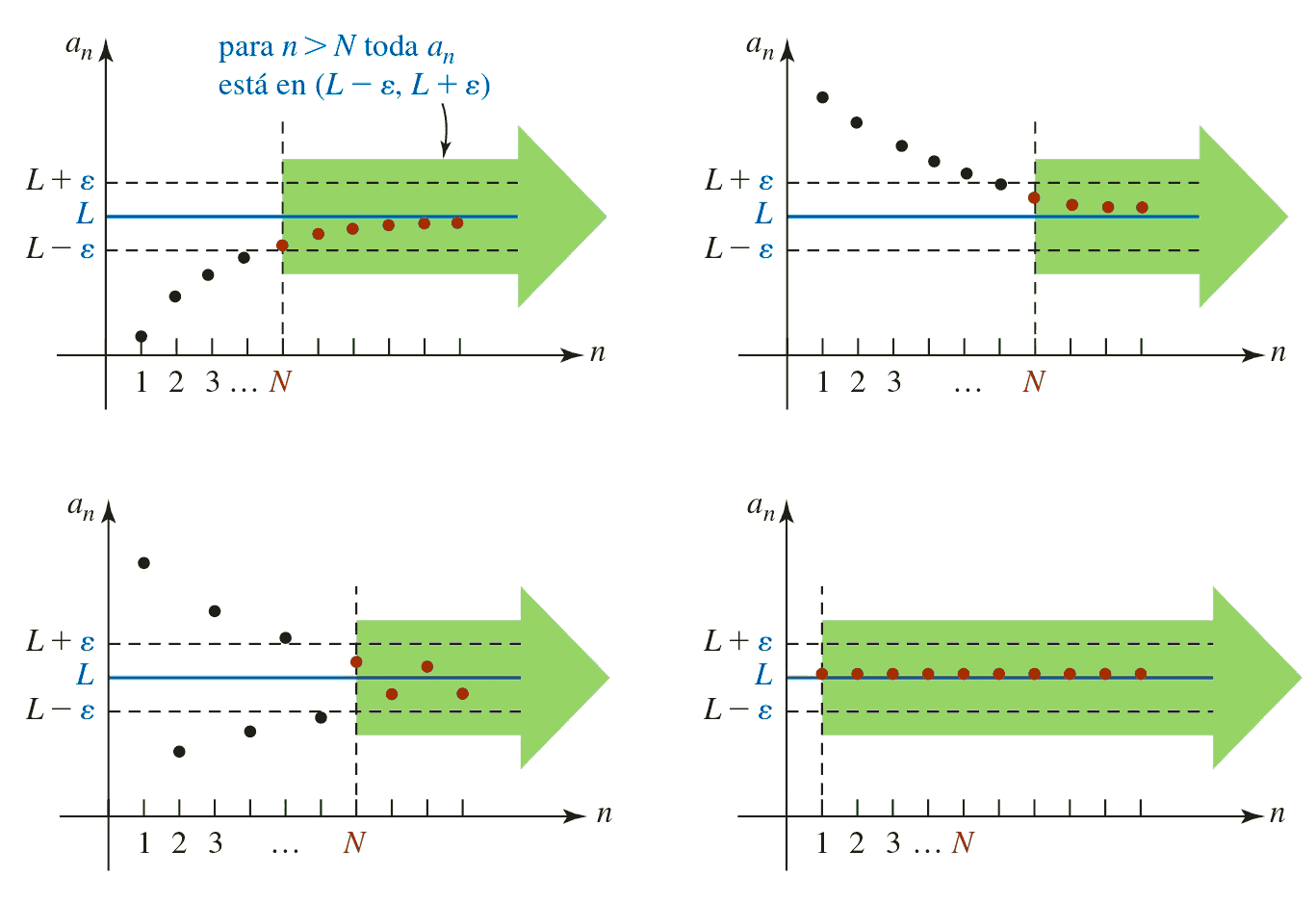
La expresión "|an - L| < ε siempre que n > N" es equivalente a decir que los términos de la sucesión que van después de N se encuentran dentro del intervalo (L - ε, L + ε). Dicho de otra manera, si comenzamos a mirar la sucesión desde el término N en adelante, todos los valores quedarán atrapados en ese rango.
La siguiente figura ilustra varias maneras en las cuales una sucesión puede converger a un número. Los puntos rojos a partir de un número N se encuentran dentro del intervalo generado por épsilon.
Si localizamos los términos de la sucesión en una recta numérica, la definición de límite nos dice que no importa qué tan pequeño se elija un intervalo (L - ε, L+ ε), existe una N tal que todos los términos de la sucesión desde aN+1 en adelante deben estar en ese intervalo.
Ejemplo 1
Antes dijimos que la sucesión con término enésimo \(a_n=\dfrac{1}{n}\) converge al límite 0. Podemos observar este comportamiento en la siguiente tabla.
| n | an |
|---|---|
| 1 | 1 |
| 2 | 1/2 = 0,5 |
| 3 | 1/3 ≈ 0,33 |
| 4 | 1/4 = 0,25 |
| … | … |
| 100 | 1/100 = 0,01 |
| … | … |
| 1000 | 1/1000 = 0,001 |
| … | … |
| 10 000 | 1/10000 = 0,0001 |
| … | … |
Para probar formalmente que el límite es 0, debemos demostrar que para todo ε > 0 existe un N tal que todos los términos después de N (n > N) verifican |1/n - 0| < ε.
La última expresión es igual a |1/n| < ε y como 1/n siempre es mayor que cero, podemos eliminar el valor absoluto:
\(\dfrac{1}{n}<ε\)
Reacomodando:
\(\dfrac{1}{ε}<n\)
Es decir, n debe ser mayor a 1/ε para que se cumpla la definición. Haciendo N = 1/ε hemos demostrado que el límite es cero, ya que para cualquier épsilon podemos encontrar un N.
Por ejemplo, si hacemos ε = 0,01, bastará tomar N = 1 / 0,01 = 100. Es decir, para todo n > 100, se cumplirá que |1/n - 0| < ε. Probemos con n = 101, entonces |1 / 101| ≈ 0,009 < 0,01 = ε y así para cualquier número épsilon positivo.
Ejemplo 2
Consideremos la sucesión con término enésimo \(a_n=\dfrac{n}{n+1}.\) Intuitivamente, podemos observar que a medida que n crece, el término an se aproxima a 1. Esto se puede ver en la siguiente tabla:
| n | an |
|---|---|
| 1 | 1 |
| 2 | 1/2 = 0,5 |
| 3 | 2/3 ≈ 0,66 |
| 4 | 3/4 = 0,75 |
| … | … |
| 100 | 100/101 ≈ 0,99 |
| … | … |
| 1000 | 1000/1001 ≈ 0,999 |
| … | … |
Para demostrar que el límite es 1, debemos probar que para todo \(\varepsilon>0,\) existe un \(N\) tal que para todo \(n>N,\) se cumple:
\(\left| \dfrac{n}{n+1}-1 \right|<\varepsilon\)
Simplificando la expresión dentro del valor absoluto:
\(\left| \dfrac{n-(n+1)}{n+1} \right|=\left| \dfrac{-1}{n+1} \right|=\dfrac{1}{n+1}\)
Entonces, nos queda:
\(\dfrac{1}{n+1}<\varepsilon\)
Reacomodando la desigualdad:
\(n+1>\dfrac{1}{\varepsilon} \quad → \quad n>\dfrac{1}{\varepsilon}-1\)
Por lo tanto, tomando \(N=\dfrac{1}{\varepsilon}-1,\) hemos demostrado que para todo \(n>N,\) se cumple \(\left| \dfrac{n}{n+1}-1 \right|<\varepsilon.\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Utilizar la definición de límite implica primero conocer un valor posible del límite y luego demostrar que se cumple lo necesario con épsilon y N. Es por esto que, en la práctica, no se usa la definición, sino que se recurre a propiedades que nos permiten calcularlo de forma más sencilla.
Límites infinitos
Si una sucesión no se aproxima a ningún número finito, sino que sus términos crecen sin límite en valor absoluto, decimos que diverge. En particular, si los términos aumentan indefinidamente, la sucesión diverge a infinito \((+\infty),\) y si disminuyen sin límite, diverge a menos infinito \((-\infty).\) En ambos casos, no existe un límite finito, pero la tendencia de crecimiento o decrecimiento ilimitado se simboliza respectivamente así:
\(\lim_{n\to \infty}a_n=\infty \quad o \quad \lim_{n\to \infty}a_n=-\infty\)
Del mismo modo que antes, tenemos una definición formal para ambos casos:
- \(\lim_{n\to \infty}a_n=+\infty\) significa que para todo número positivo M existe un entero N tal que, si n > N, entonces an > M. Esto indica que los términos de la sucesión pueden hacerse tan grandes como se quiera a partir de cierto índice.
- \(\lim_{n\to \infty}a_n=-\infty\) significa que para todo número positivo M existe un entero N tal que, si n > N, entonces an < -M. Esto indica que los términos de la sucesión pueden hacerse tan negativos como se quiera a partir de cierto índice.
En ambos casos, la sucesión es divergente.
Ejemplos
- La sucesión (n2) = (1, 4, 9, 16, …) tiene límite infinito porque sus términos crecen sin cota al avanzar en la sucesión, simbólicamente: \(\lim_{n\to \infty} n^2=+\infty.\)
- La secuencia (-2n) = (-2, -4, -6, -8, …) diverge a menos infinito porque sus términos se hacen cada vez más negativos: \(\lim_{n\to \infty} -2n=-\infty.\)
Cómo calcular el límite
Para calcular el límite de una sucesión, es fundamental observar cómo se comportan sus términos a medida que el índice n tiende al infinito. En muchas ocasiones, podemos utilizar límites ya conocidos y propiedades algebraicas que nos permiten simplificar o descomponer la expresión de la sucesión.
Cuando nos encontramos con indeterminaciones, podemos recurrir a herramientas como la regla de L'Hôpital o emplear técnicas de factorización y racionalización. Además, hay teoremas útiles que nos ayudan a respaldar los resultados obtenidos.
Ejemplo 1
Calcular \(\lim_{n\to \infty} \dfrac{4}{n+1}\)
Solución
Cuando n crece, el denominador de la fracción \(\dfrac{4}{n+1}\) se hace cada vez más grande, mientras que el numerador se mantiene igual. Por eso, la fracción se vuelve más cercana a cero. Podemos decir entonces que el límite es cero.
\(\lim_{n\to \infty} \dfrac{4}{n+1}=0\)
Nota: en la práctica puede ser de utilidad "sustituir" el símbolo de infinito en la fórmula y analizar cómo se comporta, y así detectar rápidamente indeterminaciones o límites directos. De esta forma, en el límite anterior pudimos haberlo pensado como:
\(\lim_{n\to \infty} \dfrac{4}{n+1}=\dfrac{4}{\infty + 1}=\dfrac{4}{\infty}=0\)
Las expresiones que tratan a infinito como un número no son formalmente correctas ya que infinito no es un número, sino una noción, pero pueden utilizarse como cálculo auxiliar.
Ejemplo 2
Determinar \(\lim_{n\to \infty} \dfrac{n+2}{n+1}\)
Solución
Observamos que tanto el numerador como el denominador del término general tienden a infinito, por tanto nos encontramos con una forma indeterminada ∞ / ∞. Podemos salvar esta indeterminación de la misma forma que hacíamos con funciones de variable real: dividiendo numerador y denominador por la variable elevada a la máxima potencia de la expresión, en este caso, 1.
\(\lim_{n\to \infty} \dfrac{n+2}{n+1}=\lim_{n\to \infty} \dfrac{\frac{n}{n}+\frac{2}{n}}{\frac{n}{n}+\frac{1}{n}}=\lim_{n\to \infty} \dfrac{1+\frac{2}{n}}{1+\frac{1}{n}}\)
Las expresiones 2/n y 1/n tienden a cero cuando n tiende a infinito, por tanto tenemos:
\(\lim_{n\to \infty} \dfrac{1+\frac{2}{n}}{1+\frac{1}{n}}=\dfrac{1}{1}=1\)
Ejemplo 3
Determinar si la sucesión \(\left(\dfrac{n}{\sqrt{10+n}}\right)\) es convergente o divergente.
Solución
Debemos determinar si existe \(\lim_{n\to \infty} \dfrac{n}{\sqrt{10+n}}\)
Como en el caso anterior, tanto el numerador como el denominador tienden a infinito cuando n se hace grande, causando una indeterminación ∞/∞. La salvamos dividiendo numerador y denominador entre n:
\(\lim_{n\to \infty} \dfrac{n}{\sqrt{10+n}}=\lim_{n\to \infty}\dfrac{\frac{n}{n}}{\frac{\sqrt{10+n}}{n}}=\lim_{n\to \infty}\dfrac{1}{\sqrt{\frac{10}{n^2}+\frac{1}{n}}}\)
Dentro de la raíz, \(10/n^2→0\) y \(1/n →0\) cuando \(n→\infty,\) por tanto, el denominador tiende a cero. Como el numerador es constante, toda la expresión tiende a infinito:
\(\lim_{n\to \infty}\dfrac{1}{\sqrt{\frac{10}{n^2}+\frac{1}{n}}}=\infty\)
Concluimos que la sucesión diverge a infinito.
Nota: usando la forma intuitiva podríamos hacer lo siguiente y llegar al mismo resultado.
\(\lim_{n\to \infty}\dfrac{1}{\sqrt{\frac{10}{n^2}+\frac{1}{n}}}=\dfrac{1}{\sqrt{\frac{10}{\infty}+\frac{1}{\infty}}}=\dfrac{1}{\sqrt{0+0}}=\dfrac{1}{0}=\infty\)
Límites de sucesiones conocidas
- Límite de una sucesión constante: \(\lim_{n \to \infty} k=k\) para todo número real k.
- Límite de la sucesión inversa de una potencia: \(\lim_{n \to \infty} \dfrac{1}{n^r}=0\) si r > 0. Si r < 0 la sucesión diverge a infinito.
- Límite de una progresión geométrica: \(\lim_{n \to \infty} r^n=0\) si |r| < 1. Si |r| > 1 la sucesión diverge a infinito. Si r = 1, la sucesión converge a 1.
- Límite de logaritmo sobre potencia: \(\lim_{n \to \infty} \dfrac{(\log n)^a}{n^b}=0\) para todo a > 0, b > 0.
- Límite de la raíz enésima de n: \(\lim_{n \to \infty} \sqrt[n]{n}=1\)
- Límite que define el número e: \(\lim_{n \to \infty} \left(1+\dfrac{a}{n}\right)^n=e^a\) para todo real a, siendo e el número de Euler.
Ejemplos
- La sucesión \((e^{-n})\) converge a 0 por la tercera propiedad ya que \(e^{-1}=\left(\dfrac{1}{e}\right)^n\) es una progresión geométrica con razón \(r=1/e≈0,37<1.\)
- La sucesión \(\left(\left(\dfrac{3}{2}\right)^n\right)\) diverge por ser una progresión geométrica donde \(r=\dfrac{3}{2}>1.\)
- La sucesión con fórmula \(a_n=\dfrac{5}{n^{5/2}}\) converge a 0 por la segunda propiedad ya que \(r=5/2>0.\)
- La sucesión con enésimo término \(a_n=\left(1+\dfrac{1}{n}\right)^n\) converge al número e ≈ 2,72 por la sexta propiedad.
En las sucesiones donde el término general es un cociente de dos polinomios, podemos determinar el límite fijándonos en los grados de cada uno.
- Si el grado de polinomio numerador es menor que el grado del polinomio del denominador, entonces la sucesión es convergente con límite 0. Por ejemplo: (1 / n).
- Si el grado del polinomio del numerador es mayor que el grado del polinomio del denominador, entonces la sucesión diverge a \(+\infty\) o \(-\infty\) dependiendo del signo del cociente entre los términos principales de los polinomios. Por ejemplo, (-n2 / 5n) diverge a \(-\infty.\)
- Si los grados del polinomio numerador y denominador son iguales, entonces la sucesión converge y el límite es el cociente entre los coeficientes de los términos principales (los de grado mayor). Por ejemplo, \(\left(\dfrac{2n^2+5n}{3n^2-7}\right)\) converge a 2/3.
Ejemplo
Calcular \(\lim_{n\to \infty} \dfrac{5n^2+6n-5}{-4n^2+n-19}\)
Solución
Dado que el numerador y el denominador tienen el mismo grado, calculamos el cociente de los coeficientes de los términos principales de cada uno, esto es, los de grado más grande. En el numerador el coeficiente del término principal es 5, en el denominador es -4. Su cociente es -5/4, es decir:
\(\lim_{n\to \infty}\dfrac{5n^2+6n-5}{-4n^2+n-19}=-\dfrac{5}{4}\)
Nota: los límites de este tipo pueden resolverse con el análisis de coeficientes pero también dividiendo numerador y denominador por la variable elevada a la máxima potencia presente, como hicimos en ejemplos anteriores.
Indeterminaciones
Al calcular el límite de una sucesión, pueden aparecer las siguientes formas indeterminadas:
\(\dfrac{∞}{∞},~ \dfrac{0}{0},~ 0⋅∞,~ ∞-∞,~ 1^∞,~ 0^0,~ ∞^0\)
Se llaman formas indeterminadas porque no podemos conocer el valor del límite a priori, sino que debemos efectuar algún paso previo para calcularlo.
Las formas cero sobre cero (0/0) e infinito sobre infinito (∞/∞) suelen resolverse mediante factorización, simplificación de términos, multiplicación por el conjugado o dividiendo numerador y denominador por la variable elevada a la mayor potencia presente. Las demás formas generalmente se transforman en los casos anteriores para poder aplicar técnicas algebraicas.
En los casos donde el término general de la sucesión pueda tratarse como una función real derivable, es posible emplear la regla de L’Hospital para resolver indeterminaciones del tipo 0/0 y ∞/∞.
Ejemplo 1
Resolver \(\lim_{n \to \infty} \dfrac{\sqrt{n}}{\sqrt{n}+1}\)
Solución
Observamos que se trata de una indeterminación infinito sobre infinito. Para calcular el límite, seguiremos un procedimiento algebraico que nos permitirá simplificar la expresión y analizar su comportamiento.
En primer lugar, observamos que tanto el numerador como el denominador contienen términos con \(\sqrt{n}=n^{1/2}.\) Dividiremos tanto el numerador como el denominador por la variable elevada a la máxima potencia presente (que en este caso es 1/2), es decir, \(\sqrt{n}.\) Esto nos da:
\(\lim_{n \to \infty} \dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n \to \infty} \dfrac{\frac{\sqrt{n}}{\sqrt{n}}}{\frac{\sqrt{n}}{\sqrt{n}}+\frac{1}{\sqrt{n}}}\)
\(\lim_{n \to \infty}=\dfrac{1}{1+\frac{1}{\sqrt{n}}}\)
Ahora, analizamos el comportamiento de cada término cuando \(n\) tiende a infinito. El término \(\dfrac{1}{\sqrt{n}}\) se aproxima a 0, ya que el denominador crece indefinidamente. Por lo tanto, la expresión simplificada queda:
\(\lim_{n \to \infty} \dfrac{1}{1+\dfrac{1}{\sqrt{n}}}=\dfrac{1}{1+0}=1\)
Ejemplo 2
Determinar el límite \(\lim_{n \to \infty} \dfrac{\sqrt{n+1}}{-2n+1}\)
Solución
Este límite contiene raíces y nos encontramos con una indeterminación ∞/∞. El exponente más grande en la expresión es 1, así que dividiremos numerador y denominador por n para simplificar la expresión:
\(\dfrac{\sqrt{n+1}}{-2n+1}=\dfrac{\frac{\sqrt{n+1}}{n}}{\frac{-2n}{n}+\frac{1}{n}}=\dfrac{\sqrt{\frac{n+1}{n^2}}}{-2+\frac{1}{n}}=\dfrac{\sqrt{\frac{1}{n}+\frac{1}{n^2}}}{-2+\frac{1}{n}}\)
Cuando \(n \to \infty\), \(\dfrac{1}{n} \to 0\) y \(\dfrac{1}{n^2} \to 0,\) por lo que el numerador tiende a \(\sqrt{0}=0.\) El denominador tiende a \(-2+0=-2.\) Por lo tanto, el límite queda:
\(\lim_{n \to \infty} \dfrac{\sqrt{n+1}}{-2n+1}=\dfrac{0}{-2}=0\)
En conclusión, la sucesión converge a 0.
Ejemplo 3
Obtener \(\lim_{n \to \infty} \sqrt{n+1}-\sqrt{n}\)
Solución
Cuando \(n \to \infty,\) la expresión adquiere la forma indeterminada \(\infty-\infty.\) En los límites donde aparecen raíces cuadradas suele funcionar la técnica de multiplicar y dividir la ecuación por el conjugado de la expresión con raíces. Entonces:
\(\lim_{n \to \infty} \sqrt{n+1}-\sqrt{n}=\lim_{n \to \infty} (\sqrt{n+1}-\sqrt{n})\cdot \dfrac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}\)
Ahora, aplicando la propiedad de diferencia de cuadrados podemos reescribir el numerador:
\(\lim_{n \to \infty} (\sqrt{n+1}-\sqrt{n})\cdot \dfrac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}=\lim_{n \to \infty} \dfrac{(\sqrt{n+1})^2-(\sqrt{n})^2}{\sqrt{n+1}+\sqrt{n}}\)
\(=\lim_{n \to \infty} \dfrac{n+1-n}{\sqrt{n+1}+\sqrt{n}}=\lim_{n \to \infty} \dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Ahora, el denominador tiende a infinito cuando \(n \to \infty,\) y el numerador se mantiene constante, por lo tanto el límite es igual a cero:
\(\lim_{n \to \infty} \dfrac{1}{\sqrt{n+1}+\sqrt{n}}=0\)
Ejemplo 4
Determinar si la sucesión definida por \(a_n=\dfrac{n}{2^n}\) converge y, si es así, hallar el límite.
Solución
Debemos determinar si existe \(\lim_{n \to \infty} \dfrac{n}{2^n}.\) Cuando n tiende a infinito, tanto el numerador como el denominador tienden a infinito, provocando una indeterminación. Sin embargo, el numerador es una función polinómica lineal mientras que el denominador es una función exponencial con base mayor a 1, la cual crece a un ritmo más acelerado que cualquier polinómica.
Esta diferencia fundamental en las tasas de crecimiento nos indica que el denominador eventualmente dominará, haciendo que el cociente tienda a cero. Entonces, la sucesión es convergente y su límite es cero.
\(\lim_{n \to \infty} \dfrac{n}{2^n}=0\)
Uso de la regla de L'Hôpital
Si tenemos una sucesión con término general an y conseguimos encontrar una función de variable real f(x) que replique el comportamiento de an en los enteros positivos, podemos aprovechar las herramientas del cálculo de funciones reales, como la regla de L'Hôpital para resolver límites indeterminados 0/0 e ∞/∞. El teorema que habita esto es el siguiente.
Sea f una función de una variable real tal que
\(\lim_{x \to \infty} f(x)=L\)
Si \((a_n)\) es una sucesión tal que \(f(n)=a_n\) para cada entero positivo n, entonces
\(\lim_{n \to \infty} a_n=L\)
L puede ser un número real, \(\infty\) o \(-\infty.\) Dicho de otra forma, podemos calcular el límite de la función de variable real y el mismo resultado es válido para la sucesión, ya que el comportamiento de la función en el infinito se mantiene al restringirla a los enteros positivos.
Ejemplo 1
Determine \(\lim_{n \to \infty} \dfrac{\ln n}{n}\)
Solución
Observamos que tanto el numerador como el denominador tienden a infinito cuando \(n \to \infty,\) produciendo una indeterminación. No podemos aplicar directamente la regla de L'Hôpital ya que no se aplica a sucesiones, sino a funciones de variable real.
Sin embargo, la función \(f(x)=\ln x / x\) replica el comportamiento de la sucesión cuando la restringimos a los enteros positivos, así que podemos usarla como función asociada para calcular el límite mediante la regla L'Hôpital, derivando el numerador y el denominador:
\(\lim_{x \to \infty} \dfrac{\ln x}{x}=\lim_{x \to \infty} \dfrac{1/x}{1}=0\)
Entonces, \(\lim_{n \to \infty} \dfrac{\ln n}{n}=0\)
Ejemplo 2
Calcular \(\lim_{n \to \infty} \dfrac{n^2}{e^n-1}\)
Solución
Observamos que el límite tiene la forma indeterminada \(\infty / \infty.\) Como el numerador es un polinomio y el denominador contiene una exponencial con base mayor a 1 (e ≈ 2,72), podríamos usar el argumento de unos ejemplos atrás para concluir que el denominador crece más rápido que el numerador llevando a la sucesión a converger a cero.
En este caso, usaremos la regla de L'Hôpital mediante la función asociada \(f(x)=\dfrac{x^2}{e^x-1}:\)
\(\lim_{x \to \infty} \dfrac{x^2}{e^x-1}=\lim_{x \to \infty} \dfrac{2x}{e^x}\)
Como se sigue manteniendo la indeterminación, repetimos la aplicación de la regla de L'Hôpital:
\(\lim_{x \to \infty} \dfrac{2x}{e^x}=\lim_{x \to \infty} \dfrac{2}{e^x}=0\)
ya que \(e^x\to \infty\) cuando \(x\to \infty\) y el numerador se mantiene constante. Por lo tanto:
\(\lim_{n \to \infty} \dfrac{n^2}{e^n-1}=0\)
Nótese que el proceso de determinar el límite de la sucesión está estrechamente relacionado con hallar la asíntota horizontal de la función asociada, si esta existe.
Nota: el recíproco del teorema utilizado no es cierto, si \(\lim_{n \to \infty} f(n)=L\) (cuando \(n\) es natural), no necesariamente se cumple que \(\lim_{x \to \infty} f(x)=L\) (cuando \(x\) es real). Por ejemplo, consideramos \(f(x)=\sin(\pi x).\) Para \(n \in \mathbb{N}\), \(f(n)=\sin(\pi n)=0,\) por lo que la sucesión \(a_n=f(n)\) converge a 0. Sin embargo, \(\lim_{x \to \infty} \sin(\pi x)\) no existe (oscila entre -1 y 1). En otros términos, no se puede usar el límite de la sucesión para determinar el de la función de variable real, pero sí al revés.
Propiedades de los límites
Los límites de sucesiones cumplen las mismas propiedades que los límites de funciones de variable real. Si an y bn son sucesiones convergentes y c es una constante, entonces:
1) El límite de una sucesión constante es igual a la constante:
\(\lim_{n\to \infty} c=c\)
2) El límite de una constante por una sucesión es igual a la constante por el límite:
\(\lim_{n\to \infty} c\cdot a_n=c\cdot \lim_{n\to \infty} a_n\)
3) El límite de la suma (o resta) de dos sucesiones es igual a la suma (o resta) de los límites de las sucesiones:
\(\lim_{n\to \infty} a_n ± b_n=\lim_{n\to \infty} a_n ± \lim_{n\to \infty} b_n\)
4) El límite del producto de dos sucesiones es igual al producto de los límites de las sucesiones:
\(\lim_{n\to \infty} a_n \cdot b_n=\lim_{n\to \infty} a_n \cdot \lim_{n\to \infty} b_n\)
5) El límite del cociente de dos sucesiones es igual al cociente de los límites, siempre que el límite de la sucesión del denominador no sea cero:
\(\lim_{n\to \infty} \dfrac{a_n}{b_n}=\dfrac{\lim_{n\to \infty} a_n}{\lim_{n\to \infty} b_n}\) \((\text{si}~ \lim_{n\to \infty} b_n≠0)\)
6) El límite de la potencia positiva de una sucesión positiva es igual elevar el límite de la sucesión a la potencia:
\(\lim_{n\to \infty} a_n^p=[\lim_{n\to \infty} a_n]^p~~\) \((\text{si}~ p>0, a_n>0)\)
Estas propiedades se utilizan para "descomponer" límites en otros más sencillos de calcular.
Teoremas importantes
En el estudio de límites de sucesiones, ciertos teoremas y propiedades nos permiten deducir resultados sin necesidad de realizar cálculos complicados. Veremos algunos de ellos a continuación.
Teorema de compresión o del sándwich
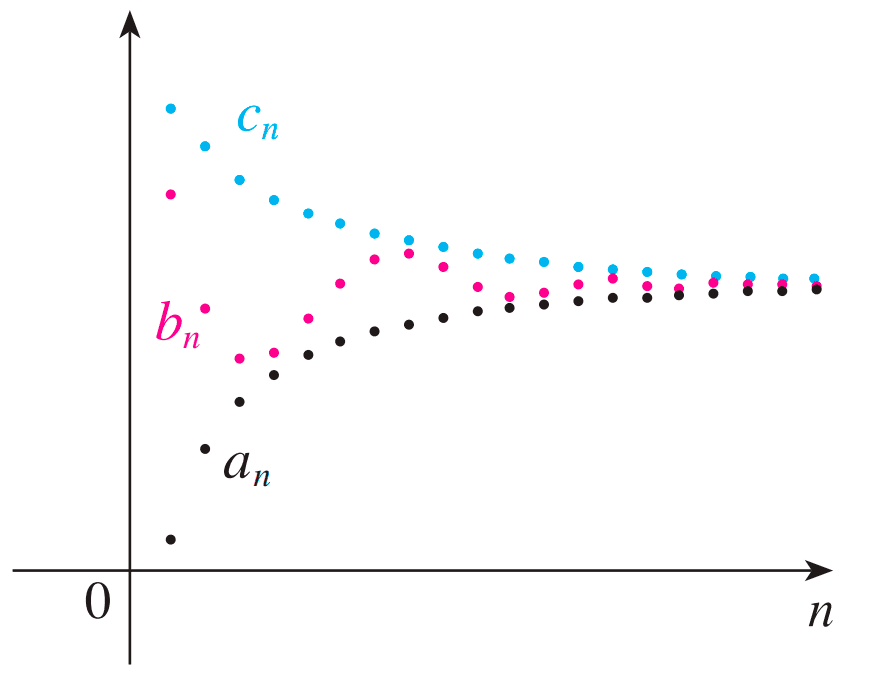
Suponga que (an), (bn) y (cn) son sucesiones tales que an ≤ bn ≤ cn para todos los valores de n mayores que algún índice N (esto es, n > N). Si (an) y (cn) convergen a un límite común L, entonces (bn) también converge a L. Es decir, si \(\lim_{n\to \infty} a_n =L~\) y \(~\lim_{n\to \infty} c_n =L,\) entonces también $$\lim_{n\to \infty} b_n =L$$
El teorema establece que, cuando una sucesión está "atrapada" entre otras dos y ambas convergen al mismo valor, la sucesión intermedia no tiene otra opción más que converger a ese mismo límite.
La utilidad del teorema radica en que, a veces, una sucesión resulta complicada de estudiar directamente. En esos casos, si conseguimos encontrar dos sucesiones más simples con límites conocidos que la encierren, podemos concluir de inmediato cuál es el límite de la sucesión intermedia.
Ejemplo 1
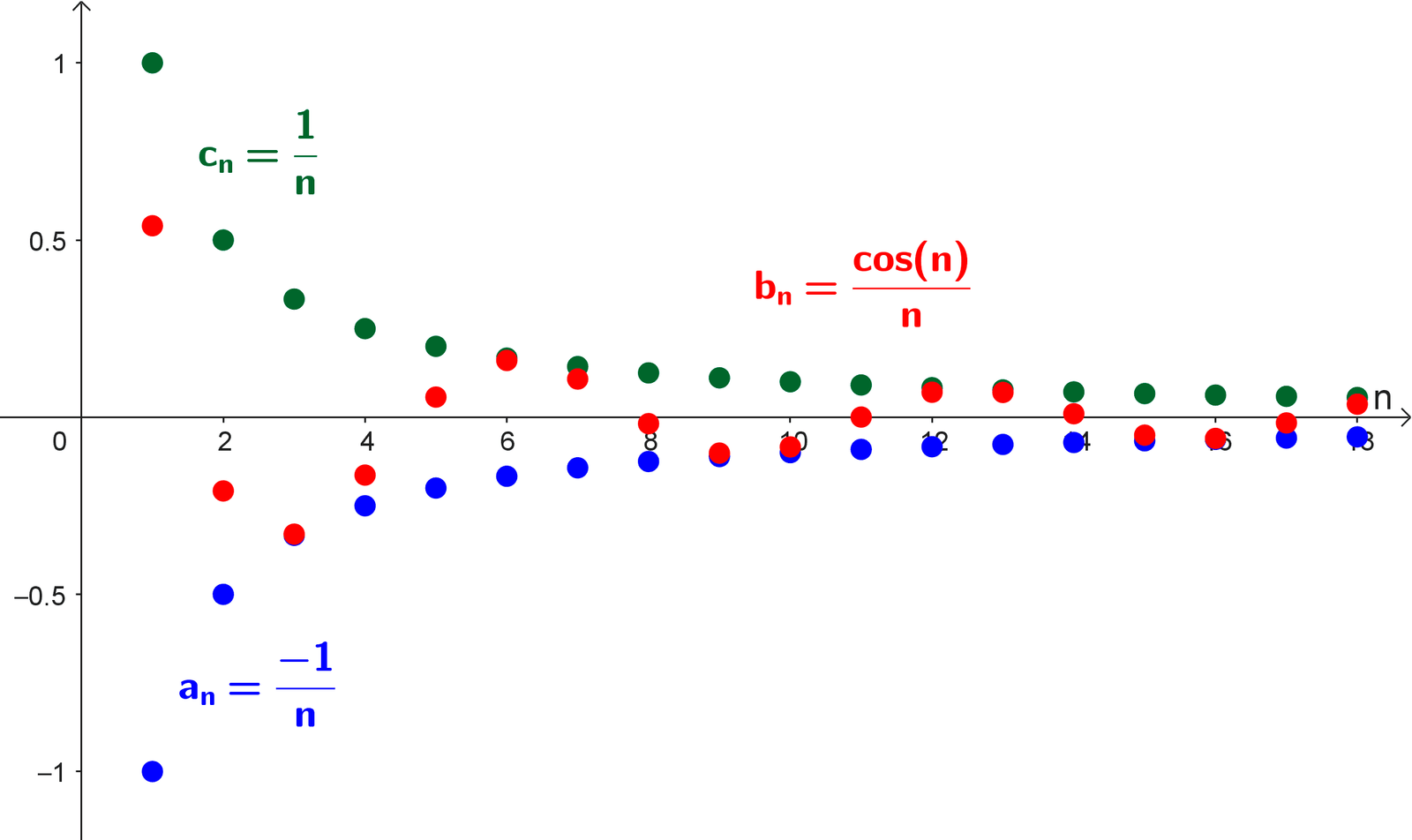
Determinar el límite de la sucesión \(\left(\dfrac{\cos(n)}{n}\right)\) si este existe.
Solución
Llamemos \(b_n\) al término general de la sucesión, entonces \(b_n=\dfrac{\cos(n)}{n}.\)
Sabemos que la función coseno está acotada entre -1 y 1 para cualquier valor real, es decir, \(-1 \leq \cos(n) \leq 1\) para todo \(n \in \mathbb{N}.\) Dividiendo cada término de esta desigualdad por \(n\) (que es positivo para \(n \geq 1\)), obtenemos:
\(\dfrac{-1}{n} \leq \dfrac{\cos(n)}{n} \leq \dfrac{1}{n}\)
Así, definimos \(a_n=\dfrac{-1}{n}\) y \(c_n=\dfrac{1}{n},\) cumpliéndose \(a_n \leq b_n \leq c_n\) para todo \(n \geq 1.\)
Ahora calculamos el límite de \(a_n\) y \(c_n\) cuando \(n\) tiende a infinito:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \left(\dfrac{-1}{n} \right)=0\)
\(\lim_{n \to \infty} c_n=\lim_{n \to \infty} \left(\dfrac{1}{n} \right)=0\)
Ambos límites son iguales a 0. Por el teorema del sándwich, como \(a_n \leq \dfrac{\cos(n)}{n} \leq c_n\) y los límites de las sucesiones que la acotan son 0, concluimos que:
\(\lim_{n \to \infty} \dfrac{\cos(n)}{n}=0\)
Este resultado es intuitivo: aunque \(\cos(n)\) oscila entre -1 y 1, el denominador \(n\) crece indefinidamente, por lo que la amplitud de las oscilaciones se reduce progresivamente, tendiendo a cero.
Ejemplo 2
Calcular el límite de la sucesión \(a_n=\dfrac{n!}{n^n}\) si existe.
Solución
Tanto numerador como denominador se aproximan al infinito cuando \(n \to \infty,\) pero no podemos utilizar la regla de L'Hospital porque el factorial no está definido para números no naturales.
Escribamos algunos términos para ver si es posible intuir qué pasa con \(a_n\) cuando \(n\) es muy grande:
\(a_1=1 \quad a_2=\dfrac{1 \cdot 2}{2 \cdot 2} \quad a_3=\dfrac{1 \cdot 2 \cdot 3}{3 \cdot 3 \cdot 3}\)
\(a_n=\dfrac{1 \cdot 2 \cdot 3 \cdot ~\cdots~ \cdot n}{n \cdot n \cdot n \cdot ~\cdots~ \cdot n}\)
Podemos escribirlo como:
\(a_n=\dfrac{1}{n} \left(\dfrac{2 \cdot 3 \cdot ~\cdots~ \cdot n}{n \cdot n \cdot ~\cdots~ \cdot n} \right)\)
La expresión entre paréntesis es a lo sumo 1 porque el numerador es menor (o igual) al denominador. Y, como la sucesión no puede tomar valores negativos, nos queda
\(0<a_n \leq \dfrac{1}{n}\)
Sabemos que \(1/n \to 0\) cuando \(n \to \infty,\) así que \(a_n \to 0\) cuando \(n \to \infty\) por el teorema de compresión.
\(\lim_{n \to \infty} \dfrac{n!}{n^n}=0\)
Teorema del valor absoluto
Si la sucesión de valores absolutos ( |an| ) converge a 0, entonces la sucesión (an) converge a 0.
Ejemplo
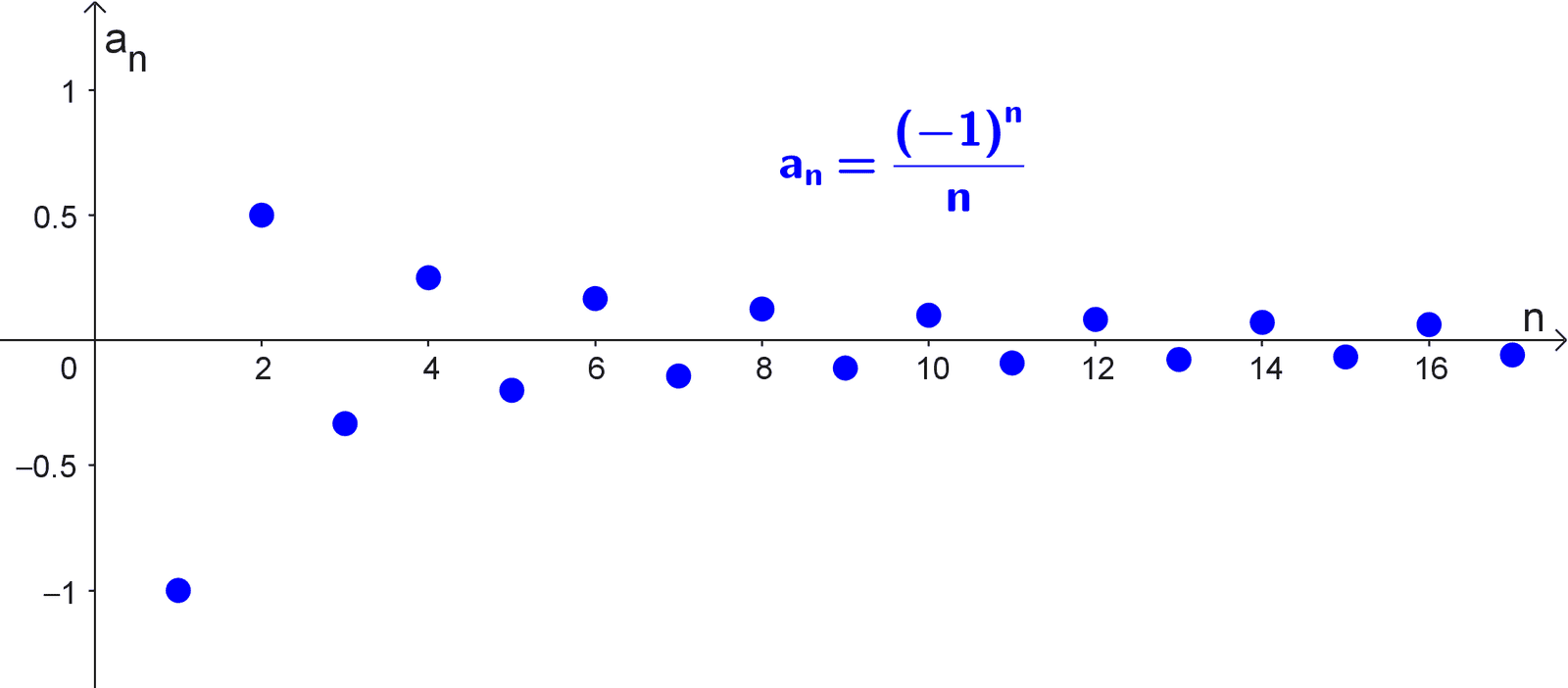
Evaluar \(\lim_{n \to \infty} \dfrac{(-1)^n}{n}\) si existe.
Solución
Primero, calculamos el límite del valor absoluto:
\(\lim_{n \to \infty} \left|\dfrac{(-1)^n}{n}\right|=\lim_{n \to \infty} \dfrac{1}{n}=0\)
De acuerdo al teorema del valor absoluto:
\(\lim_{n \to \infty} \dfrac{(-1)^n}{n}=0\)
Teorema de la función continua
Si acoplamos una función continua a los términos de una sucesión convergente, el resultado también es convergente. Si \(\lim_{n\to \infty} a_n=L\) y la función f es continua en L, entonces \(\lim_{n\to \infty} f(a_n)=f(L)\)
Ejemplo
Determinar \(\lim_{n \to \infty} \sin(\pi / n)\)
Solución
Cuando \(n\to \infty, \pi / n \to 0,\) y como la función seno es continua en 0, el teorema nos permite escribir
\(\lim_{n \to \infty} \sin(\pi / n)=\sin(\lim_{n \to \infty} (\pi / n))=\sin 0=0\)
Otros teoremas
- Si una sucesión es acotada y monótona, entonces converge. Si es creciente converge al supremo de la sucesión y si es decreciente converge al ínfimo.
- La suma o resta entre una sucesión acotada y una que diverge a más o menos infinito, diverge a más o menos infinito (acotada ± ∞ = ± ∞).
- El producto entre una sucesión que converge a cero y una acotada, converge a cero (0 ⋅ acotada = 0).
- El cociente entre una sucesión acotada y una que diverge a infinito, converge a cero (acotada / ∞ = 0).
- La suma de dos sucesiones que divergen a infinito, diverge a infinito (∞ + ∞ = ∞).
Ejercicios resueltos
Calcular el límite de las siguientes sucesiones (si existe) dados sus términos generales.
- \(a_n=\dfrac{n}{n+1}-\dfrac{n+1}{n}\)
- \(a_n=\cos\left(\dfrac{n\pi}{2}\right)\)
- \(a_n=\dfrac{n^2+3n-2}{5n^2+6}\)
- \(a_n=3+(-1)^n\)
- \(a_n=\dfrac{1+(-1)^n}{n}\)
- \(a_n=\dfrac{3^n+(-2)^n}{3^{n+1}+(-2)^{n+1}}\)
- \(a_n=\dfrac{2-3e^{-n}}{6+4e^{-n}} \)
- \(a_n=\left(1+\dfrac{2}{n}\right)^n \)
- \(a_n=2^{1/n} \)
- \(a_n=10^{(n+1)/n}\)
- \(a_n=\sqrt{\dfrac{n+1}{n^2+2n+1}}\)
- \(a_n=\sqrt{n(n+4)}-n\)
- \(a_n=\sqrt{n+\sqrt{n}}-\sqrt{n-\sqrt{n}}\)
- \(a_n=n\left(\dfrac{1+(-1)^n}{3}\right)^n \)
- \(a_n=n^2\left(\dfrac{1+n}{3n}\right)^n\)
- \(a_n=\dfrac{\ln n}{\ln 3n}\)
- \(a_n=\ln\left(\dfrac{4n+1}{3n-1}\right)\)
Soluciones
Solución 1
Sucesión dada: \(a_n=\dfrac{n}{n+1}-\dfrac{n+1}{n}\)
Para calcular el límite cuando \(n\) tiende a infinito, podemos analizar el comportamiento de cada término por separado. Este enfoque es válido porque el límite de una diferencia es igual a la diferencia de los límites, siempre que estos últimos existan.
Primero, calculamos el límite del término \(\dfrac{n}{n+1}.\) Para ello, dividimos tanto el numerador como el denominador entre \(n,\) que es la máxima potencia de \(n\) en la expresión:
\(\lim_{n \to \infty} \dfrac{n}{n+1}=\lim_{n \to \infty} \dfrac{\dfrac{n}{n}}{\dfrac{n}{n}+\dfrac{1}{n}}=\lim_{n \to \infty} \dfrac{1}{1+\dfrac{1}{n}}\)
Dado que \(\dfrac{1}{n} \to 0\) cuando \(n \to \infty,\) obtenemos:
\(\lim_{n \to \infty} \dfrac{1}{1+0}=\dfrac{1}{1}=1\)
A continuación, calculamos el límite del término \(\dfrac{n+1}{n}.\) Podemos reescribir la fórmula de la siguiente manera:
\(\lim_{n \to \infty} \dfrac{n+1}{n}=\lim_{n \to \infty} \left(\dfrac{n}{n}+\dfrac{1}{n} \right)=\lim_{n \to \infty} \left(1+\dfrac{1}{n} \right)\)
Nuevamente, como \(\dfrac{1}{n} \to 0,\) el resultado es:
\(\lim_{n \to \infty} \left(1+0 \right)=1\)
Ahora, aplicamos la propiedad de que el límite de una diferencia es la diferencia de los límites:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \left(\dfrac{n}{n+1} \right)-\lim_{n \to \infty} \left(\dfrac{n+1}{n} \right)=1-1=0\)
Por lo tanto, el límite de la sucesión \(\dfrac{n}{n+1}-\dfrac{n+1}{n}\) cuando \(n\) tiende a infinito es 0.
Solución 2
Sucesión dada: \(a_n=\cos\left(\dfrac{n\pi}{2}\right)\)
Analizamos los términos de la sucesión para valores crecientes de \(n,\) observando que la función coseno depende del argumento \(n\pi /2,\) cuyo valor cambia periódicamente con \(n.\) Calculamos los primeros términos para identificar un patrón:
- Para \(n=1\): \(a_1=\cos\left(\dfrac{\pi}{2}\right)=0\)
- Para \(n=2\): \(a_2=\cos(\pi)=-1\)
- Para \(n=3\): \(a_3=\cos\left(\dfrac{3\pi}{2}\right)=0\)
- Para \(n=4\): \(a_4=\cos(2\pi)=1\)
- Para \(n=5\): \(a_5=\cos\left(\dfrac{5\pi}{2}\right)=0\)
- Para \(n=6\): \(a_6=\cos(3\pi)=-1\)
Se observa que los valores de \(a_n\) oscilan entre \(-1\), \(0\) y \(1,\) sin tender a un único valor fijo cuando \(n\) aumenta. Dado que no existe un número real \(L\) tal que todos los términos se acerquen a \(L\) para \(n\) suficientemente grande, concluimos que la sucesión oscila y, por lo tanto, diverge.
Solución 3
Sucesión dada: \(a_n=\dfrac{n^2+3n-2}{5n^2+6}\)
Para hallar el límite cuando \(n \to \infty,\) dividimos tanto el numerador como el denominador entre \(n^2,\) que es la potencia dominante en la expresión. Realizamos la división término a término:
\(a_n=\dfrac{n^2+3n-2}{5n^2+6}=\dfrac{\dfrac{n^2}{n^2}+\dfrac{3n}{n^2}-\dfrac{2}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{6}{n^2}}=\dfrac{1+\dfrac{3}{n}-\dfrac{2}{n^2}}{5+\dfrac{6}{n^2}}\)
Ahora, calculamos el límite cuando \(n \to \infty.\) Observamos que los términos \(\dfrac{3}{n}\), \(\dfrac{2}{n^2}\) y \(\dfrac{6}{n^2}\) tienden a 0, ya que el denominador crece indefinidamente mientras el numerador permanece constante. Por lo tanto:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{1+\dfrac{3}{n}-\dfrac{2}{n^2}}{5+\dfrac{6}{n^2}}=\dfrac{1+0-0}{5+0}=\dfrac{1}{5}\)
Así, la sucesión converge a \(\dfrac{1}{5}.\)
Solución 4
Sucesión dada: \(a_n=3+(-1)^n\)
Analizamos los términos de la sucesión para valores de \(n.\) Notamos que \((-1)^n\) alterna entre \(-1\) y \(1\) dependiendo de si \(n\) es par o impar:
Si \(n\) es par: \((-1)^n=1,\) entonces \(a_n=3+1=4\)
Si \(n\) es impar: \((-1)^n=-1,\) entonces \(a_n=3-1=2\)
Así, la sucesión oscila entre 2 y 4, sin tender a un único valor. Por tanto, la sucesión diverge.
Solución 5
Sucesión dada: \(a_n=\dfrac{1+(-1)^n}{n}\)
Podemos separar la expresión en dos términos:
\(a_n=\dfrac{1}{n}+\dfrac{(-1)^n}{n}\)
Calculamos el límite de cada término por separado cuando \(n \to \infty:\)
\(\lim_{n \to \infty} \dfrac{1}{n}=0\)
\(\lim_{n \to \infty} \dfrac{(-1)^n}{n}=0,\) ya que \(|(-1)^n/n|=1/n \to 0\) (por el teorema del valor absoluto).
Usando la propiedad de que el límite de una suma es la suma de los límites (si ambos existen), obtenemos:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{1}{n}+\lim_{n \to \infty} \dfrac{(-1)^n}{n}=0+0=0\)
Por lo tanto, la sucesión converge a 0.
Solución 6
Sucesión dada: \(a_n=\dfrac{3^n+(-2)^n}{3^{n+1}+(-2)^{n+1}}\)
Para analizar el límite cuando \(n \to \infty,\) observamos que el término \(3^n\) domina en el numerador y \(3^{n+1}\) en el denominador, ya que \(3^n\) crece mucho más rápido que \((-2)^n,\) cuyo valor absoluto aumenta pero alterna en signo.
Sacamos factor común \(3^n\) en el numerador y en el denominador usamos propiedades de las potencias, luego dividimos numerador y denominador entre \(3^n\) para simplificar:
\(a_n=\dfrac{3^n+(-2)^n}{3^{n+1}+(-2)^{n+1}}=\dfrac{3^n \left(1+\dfrac{(-2)^n}{3^n}\right)}{3^n \cdot 3+(-2) \cdot (-2)^n}=\dfrac{1+\left(\dfrac{-2}{3}\right)^n}{3+(-2) \cdot \left(\dfrac{-2}{3}\right)^n}\)
Ahora, calculamos el límite cuando \(n \to \infty.\) Notamos que \(\left| \dfrac{-2}{3} \right|=\dfrac{2}{3}<1,\) por lo que \(\left(\dfrac{-2}{3}\right)^n \to 0.\) Así:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{1+\left(\dfrac{-2}{3}\right)^n}{3+(-2) \cdot \left(\dfrac{-2}{3}\right)^n}=\dfrac{1+0}{3+(-2) \cdot 0}=\dfrac{1}{3}\)
Por tanto, la sucesión converge a \(\dfrac{1}{3}.\)
Solución 7
Sucesión dada: \(a_n=\dfrac{2-3e^{-n}}{6+4e^{-n}}\)
Calculamos el límite cuando \(n \to \infty.\) Recordamos que \(e^{-n}=\dfrac{1}{e^n} \to 0\) cuando \(n \to \infty,\) ya que \(e^n\) crece indefinidamente. Sustituimos este comportamiento en la expresión:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{2-3e^{-n}}{6+4e^{-n}}=\dfrac{2-3 \cdot 0}{6+4 \cdot 0}=\dfrac{2}{6}=\dfrac{1}{3}\)
Así, la sucesión converge a \(\dfrac{1}{3}.\) El término \(e^{-n}\) es despreciable para \(n\) grande, por lo que el resultado depende únicamente de los términos constantes.
Solución 8
Sucesión dada: \(a_n=\left(1+\dfrac{2}{n}\right)^n\)
Reconocemos que esta expresión tiene la forma del límite notable \(\lim_{n \to \infty} \left(1+\dfrac{a}{n}\right)^n=e^a.\) En este caso, \(a=2,\) por lo que:
\(\lim_{n \to \infty} \left(1+\dfrac{2}{n}\right)^n=e^2\)
Podemos justificar esto rigurosamente mediante la definición del número \(e.\) Si hacemos el cambio de variable \(m=\dfrac{n}{2},\) entonces \(n=2m,\) y cuando \(n \to \infty,\) también \(m \to \infty.\) Sustituyendo:
\(\left(1+\dfrac{2}{n}\right)^n=\left(1+\dfrac{1}{m}\right)^{2m}=\left[\left(1+\dfrac{1}{m}\right)^m\right]^2\)
Y como \(\lim_{m \to \infty} \left(1+\dfrac{1}{m}\right)^m=e,\) tenemos:
\(\lim_{n \to \infty} a_n=\lim_{m \to \infty} \left[\left(1+\dfrac{1}{m}\right)^m\right]^2=e^2\)
Por lo tanto, la sucesión converge a \(e^2.\)
Solución 9
Sucesión dada: \(a_n=2^{1/n}\)
Calculamos el límite cuando \(n \to \infty.\) Recordamos que \(\dfrac{1}{n} \to 0\) cuando \(n \to \infty.\) Así, la expresión se reduce a \(2^0=1.\)
\(\lim_{n \to \infty} 2^{1/n}=2^0=1\)
Por tanto, la sucesión converge a 1.
Solución 10
Sucesión dada: \(a_n=10^{(n+1)/n}\)
Analizamos el exponente: \(\dfrac{n+1}{n}=1+\dfrac{1}{n}.\) Cuando \(n \to \infty\), \(\dfrac{1}{n} \to 0,\) por lo que el exponente tiende a 1. Dado que la función exponencial de base 10 es continua, podemos evaluar el límite directamente:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} 10^{1+1/n}=10^{1}=10\)
Por tanto, la sucesión converge a 10.
Solución 11
Sucesión dada: \(a_n=\sqrt{\dfrac{n+1}{n^2+2n+1}}\)
Notamos que el denominador \(n^2+2n+1=(n+1)^2.\) Así, simplificamos la expresión dentro de la raíz:
\(a_n=\sqrt{\dfrac{n+1}{(n+1)^2}}=\sqrt{\dfrac{1}{n+1}}=\dfrac{1}{\sqrt{n+1}}\)
Ahora, calculamos el límite cuando \(n \to \infty:\)
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{1}{\sqrt{n+1}}=0\)
La sucesión converge a 0, ya que el denominador crece indefinidamente.
Solución 12
Sucesión dada: \(a_n=\sqrt{n(n+4)}-n\)
Esta expresión presenta una indeterminación del tipo \(\infty-\infty\) cuando \(n \to \infty.\) Para resolverla, multiplicamos y dividimos por el conjugado:
\(a_n=\dfrac{(\sqrt{n(n+4)}-n)(\sqrt{n(n+4)}+n)}{\sqrt{n(n+4)}+n}=\dfrac{n(n+4)-n^2}{\sqrt{n(n+4)}+n}=\dfrac{n^2+4n-n^2}{\sqrt{n(n+4)}+n}=\dfrac{4n}{\sqrt{n(n+4)}+n}\)
Simplificamos factorizando \(n\) en el denominador:
\(a_n=\dfrac{4n}{n \left(\sqrt{\dfrac{n(n+4)}{n^2}}+1 \right)}=\dfrac{4}{\sqrt{1+\dfrac{4}{n}}+1}\)
Ahora, calculamos el límite cuando \(n \to \infty:\)
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \dfrac{4}{\sqrt{1+\dfrac{4}{n}}+1}=\dfrac{4}{\sqrt{1+0}+1}=\dfrac{4}{1+1}=2\)
Por tanto, la sucesión converge a 2.
Solución 13
Sucesión dada: \(a_n=\sqrt{n+\sqrt{n}}-\sqrt{n-\sqrt{n}}\)
Nuevamente, tenemos una indeterminación \(\infty-\infty.\) Multiplicamos y dividimos por el conjugado:
\(a_n=\dfrac{(\sqrt{n+\sqrt{n}}-\sqrt{n-\sqrt{n}})(\sqrt{n+\sqrt{n}}+\sqrt{n-\sqrt{n}})}{\sqrt{n+\sqrt{n}}+\sqrt{n-\sqrt{n}}}=\dfrac{(n+\sqrt{n})-(n-\sqrt{n})}{\sqrt{n+\sqrt{n}}+\sqrt{n-\sqrt{n}}}=\dfrac{2\sqrt{n}}{\sqrt{n+\sqrt{n}}+\sqrt{n-\sqrt{n}}}\)
Factorizamos \(\sqrt{n}\) en el denominador:
\(a_n=\dfrac{2\sqrt{n}}{\sqrt{n} \left(\sqrt{1+\dfrac{1}{\sqrt{n}}}+\sqrt{1-\dfrac{1}{\sqrt{n}}} \right)}=\dfrac{2}{\sqrt{1+\dfrac{1}{\sqrt{n}}}+\sqrt{1-\dfrac{1}{\sqrt{n}}}}\)
Calculamos el límite cuando \(n \to \infty.\) Notamos que \(\dfrac{1}{\sqrt{n}} \to 0:\)
\(\lim_{n \to \infty} a_n=\dfrac{2}{\sqrt{1+0}+\sqrt{1-0}}=\dfrac{2}{1+1}=1\)
La sucesión converge a 1.
Solución 14
Sucesión dada: \(a_n=n \left(\dfrac{1+(-1)^n}{3} \right)^n\)
Analizamos el comportamiento del término \(\left(\dfrac{1+(-1)^n}{3} \right)^n.\) Notamos que \(1+(-1)^n\) alterna entre 0 y 2:
Si \(n\) es impar: \((-1)^n=-1,\) entonces \(1+(-1)^n=0.\)
Si \(n\) es par: \((-1)^n=1,\) entonces \(1+(-1)^n=2.\)
Por tanto, para \(n\) impar, \(a_n=n \cdot 0^n=0.\) Para \(n\) par, \(a_n=n \left(\dfrac{2}{3} \right)^n.\)
Ahora, estudiamos el límite de la subsucesión para \(n\) par. Sea \(n=2k:\)
\(a_{2k}=2k \left(\dfrac{2}{3} \right)^{2k}=2k \left(\dfrac{4}{9} \right)^k\)
Como \(\left| \dfrac{4}{9} \right|<1\), \(\left(\dfrac{4}{9} \right)^k \to 0\) más rápido de lo que \(2k \to \infty,\) por lo que:
\(\lim_{k \to \infty} a_{2k}=0\)
Para \(n\) impar, \(a_n=0.\) Así, todas las subsucesiones convergen a 0. Por tanto, \(\lim_{n \to \infty} a_n=0.\)
Solución 15
Sucesión dada: \(a_n=n^2 \left(\dfrac{1+n}{3n} \right)^n\)
Para determinar el comportamiento de esta sucesión cuando \(n \to \infty,\) analizamos su estructura. Observamos que la expresión dentro del paréntesis puede simplificarse:
\(\dfrac{1+n}{3n}=\dfrac{n(1+\dfrac{1}{n})}{3n}=\dfrac{1}{3} \left(1+\dfrac{1}{n}\right)\)
Así, la sucesión queda como:
\(a_n=n^2 \left[ \dfrac{1}{3} \left(1+\dfrac{1}{n}\right) \right]^n=n^2 \cdot \dfrac{1}{3^n} \left(1+\dfrac{1}{n}\right)^n\)
Sabemos que \(\lim_{n \to \infty} \left(1+\dfrac{1}{n}\right)^n=e,\) por lo que el término \(\left(1+\dfrac{1}{n}\right)^n\) converge a \(e.\) Sin embargo, el factor \(n^2\) y el término \(\dfrac{1}{3^n}\) compiten en el crecimiento. Notamos que \(\dfrac{1}{3^n}\) decrece exponencialmente (ya que \(3>1\)), mientras que \(n^2\) crece polinomialmente. Para estudiar el límite, consideramos la expresión completa:
\(a_n=n^2 \cdot \dfrac{1}{3^n} \cdot \left(1+\dfrac{1}{n}\right)^n\)
Calculamos el límite:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} n^2 \cdot \dfrac{1}{3^n} \cdot e\)
Dado que \(\lim_{n \to \infty} \dfrac{n^2}{3^n}=0\) (porque la base exponencial \(3>1\) domina al polinomio \(n^2\)), y \(e\) es constante, aplicamos la propiedad del producto de límites:
\(\lim_{n \to \infty} a_n=e \cdot \lim_{n \to \infty} \dfrac{n^2}{3^n}=e \cdot 0=0\)
Por lo tanto, la sucesión converge a 0.
Solución 16
Sucesión dada: \(a_n=\dfrac{\ln n}{\ln 3n}\)
Notamos que tanto el numerador como el denominador tienden a infinito, por lo que tenemos una indeterminación del tipo \(\infty/\infty.\) Para encontrar el límite, aplicamos la regla de L'Hôpital, considerando la función asociada de variable real.
\(\lim_{n \to \infty} \dfrac{\ln n}{\ln 3n}=\lim_{x \to \infty} \dfrac{\ln x}{\ln 3x}\)
Aplicamos L'Hôpital, derivando respecto a \(x:\)
\(\dfrac{d}{dx} (\ln x)=\dfrac{1}{x}, \quad \dfrac{d}{dx} (\ln 3x)=\dfrac{1}{x}\)
Entonces,
\(\lim_{x \to \infty} \dfrac{\ln x}{\ln 3x}=\lim_{x \to \infty} \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}}=\lim_{x \to \infty} 1=1\)
Por lo tanto, la sucesión converge a 1.
\(\lim_{n \to \infty} \dfrac{\ln n}{\ln 3n}=1\)
Alternativamente, podemos usar propiedades de logaritmos:
\(\ln 3n=\ln 3+\ln n\)
Entonces,
\(a_n=\dfrac{\ln n}{\ln 3+\ln n}=\dfrac{1}{\dfrac{\ln 3}{\ln n}+1}\)
Cuando \(n \to \infty\), \(\ln n \to \infty,\) entonces \(\dfrac{\ln 3}{\ln n} \to 0,\) haciendo que \(a_n \to 1.\)
Solución 17
Sucesión dada: \(a_n=\ln \left(\dfrac{4n+1}{3n-1} \right)\)
Para calcular el límite cuando \(n \to \infty,\) usamos el teorema de la función continua. Primero, encontramos el límite del argumento del logaritmo:
\(b_n=\dfrac{4n+1}{3n-1}\)
Dividimos numerador y denominador entre \(n:\)
\(b_n=\dfrac{4+\dfrac{1}{n}}{3-\dfrac{1}{n}}\)
Entonces,
\(\lim_{n \to \infty} b_n=\dfrac{4+0}{3-0}=\dfrac{4}{3}\)
Ahora, como la función logaritmo natural \(\ln x\) es continua en \(x>0,\) y \(\dfrac{4}{3}>0,\) aplicamos el teorema:
\(\lim_{n \to \infty} a_n=\lim_{n \to \infty} \ln \left(\dfrac{4n+1}{3n-1} \right)=\ln \left(\lim_{n \to \infty} \dfrac{4n+1}{3n-1} \right)=\ln \left(\dfrac{4}{3} \right)\)
Por lo tanto, la sucesión converge a \(\ln \left(\dfrac{4}{3} \right).\)
Bibliografía
- Apostol, T. (1984). Calculus: Cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: Trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: Matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: Trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

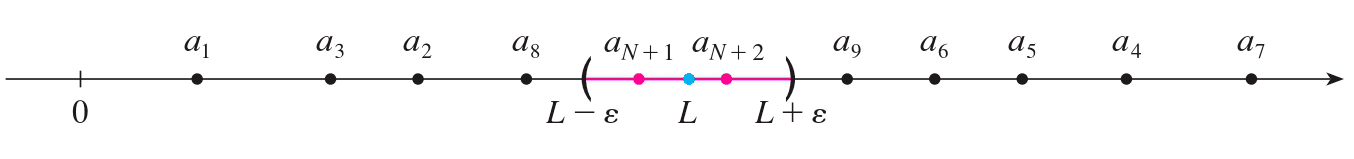
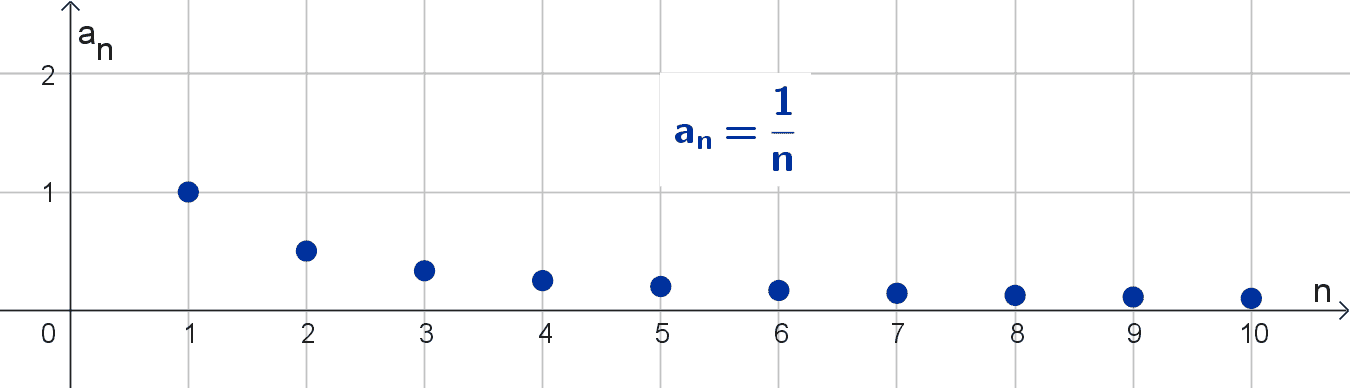
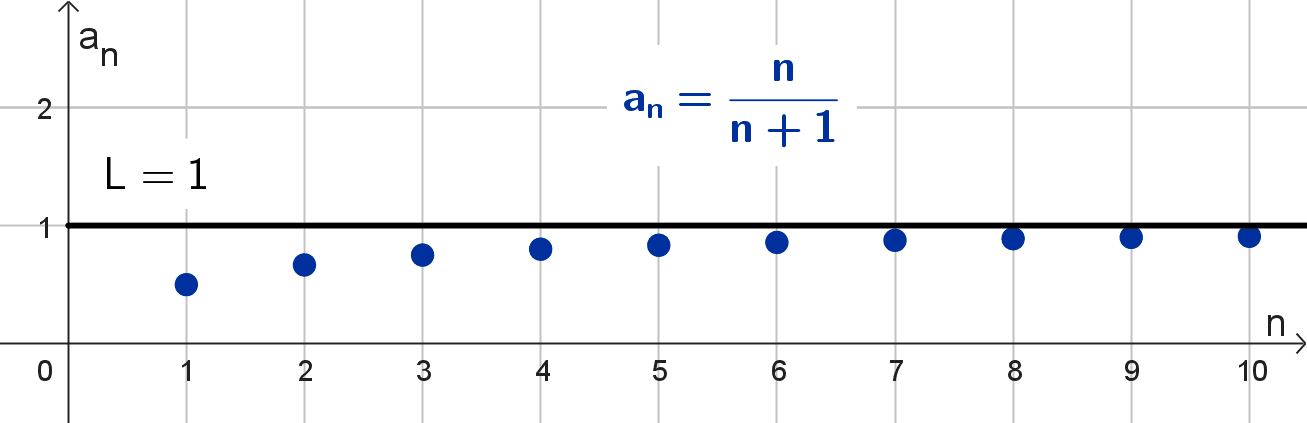
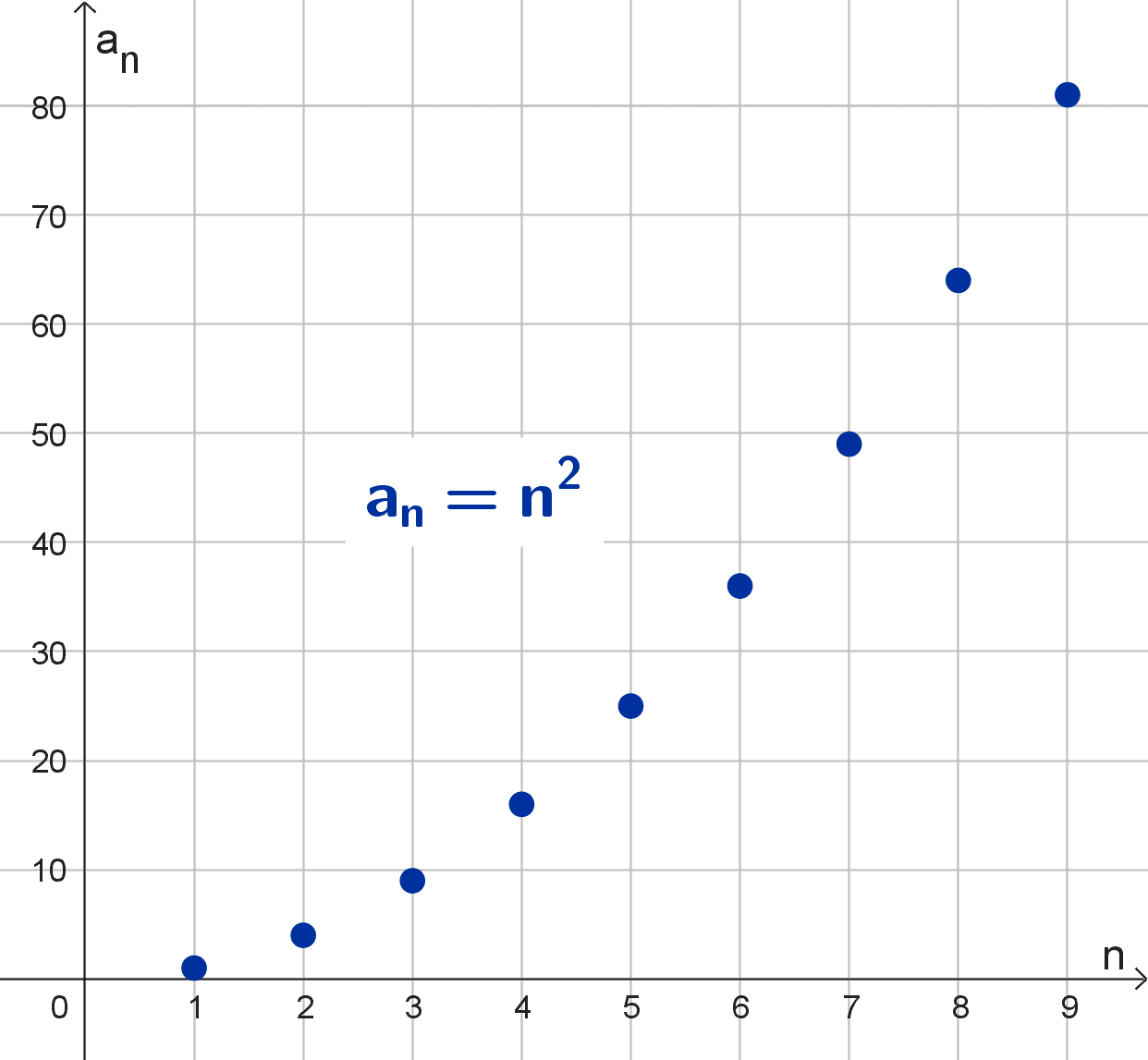
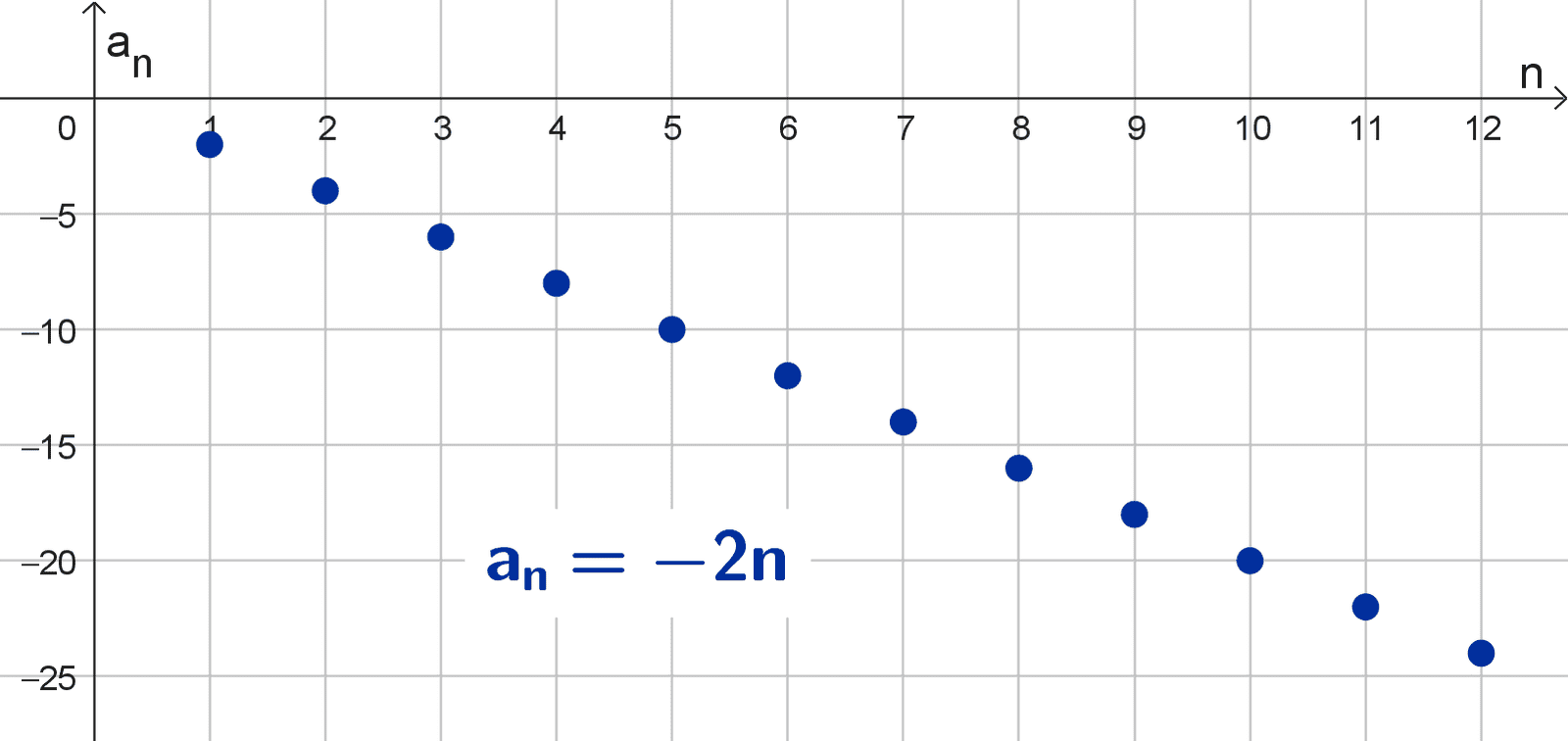
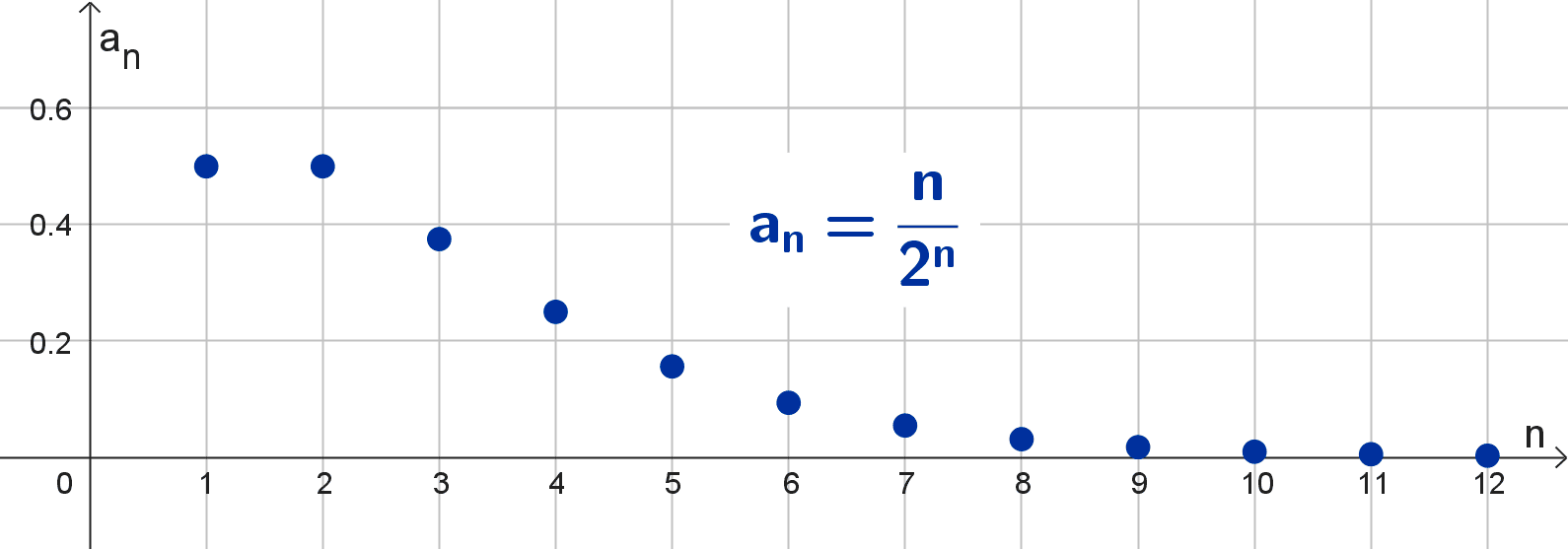
Otros artículos que pueden interesarte