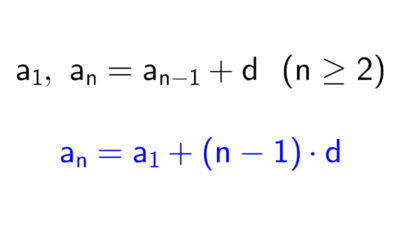
Progresión geométrica

Una sucesión o progresión geométrica (PG) es una lista ordenada de números reales en la que cada término, tras el primero, se obtiene multiplicando el término precedente por una constante fija denominada razón común, la cual se denota habitualmente con la letra r.

Por ejemplo:

1. La sucesión 3, 6, 12, 24, 48, … es una progresión geométrica con razón r = 2, observamos que cada término es el doble del anterior. El resultado es un crecimiento muy rápido conocido como crecimiento exponencial.
2. En la progresión 81, 27, 9, 3, 1, … la razón es r = 1/3. Aunque todos los términos son positivos, la secuencia es decreciente porque cada vez se multiplica por un número menor que 1, acercándose progresivamente a cero.
3. Consideremos la sucesión 3, -6, 12, -24, 48, … Aquí, la razón es r = -2. Los términos alternan su signo, oscilando entre valores positivos y negativos, mientras que su valor absoluto crece exponencialmente.
4. La secuencia 1, 1, 1, 1, … es geométrica con razón r = 1, es una sucesión constante (todos sus términos son iguales) ya que multiplicar por 1 no altera ningún valor.
5. La progresión 1; 1,5; 2,25; 3,375; … es geométrica con una razón r = 1,5.
6. La lista ordenada 100; 10; 1; 0,1; 0,01; … tiene una razón r = 0,1.

Como vemos en los ejemplos, la razón común r puede ser cualquier número real diferente de cero: positivo, negativo, entero, fraccionario, decimal, etc. La diferencia entre una progresión aritmética y una geométrica está en la operación que define su patrón: en la aritmética cada término se obtiene sumando una diferencia al anterior, mientras que en la geométrica cada término se obtiene multiplicando el anterior por una constante llamada razón.

Fórmula recursiva

La definición fundamental de una progresión geométrica se expresa de forma recursiva. Partiendo de un primer término a₁ ≠ 0, cada término siguiente se calcula multiplicando el anterior por la razón común r ≠ 0:

a₁, a_n = a_n-1 ⋅ r (para n ≥ 2)

Así, los términos son:

a₁

a₂ = a₁ ⋅ r

a₃ = a₂ ⋅ r = (a₁ ⋅ r) ⋅ r = a₁ ⋅ r²

a₄ = a₃ ⋅ r = (a₁ ⋅ r²) ⋅ r = a₁ ⋅ r³

…

a_n = a_n-1 ⋅ r

a_n+1 = a_n ⋅ r

…

Despejando r a partir de la relación recurrente obtenemos la fórmula para calcular la razón de la sucesión. Dado que a_n = a_n-1 ⋅ r, entonces:

\(r=\dfrac{a_n}{a_{n-1}}\)

Es decir, la razón común es igual al cociente entre cualquier término y su antecesor inmediato. Así, si en una sucesión este cociente no es constante para cualquier par de términos consecutivos, podemos concluir que la sucesión no es geométrica.

Nota: exigimos que tanto el primer término a₁ como la razón común r sean diferentes de cero porque en caso de que alguno de los dos sean cero se generaría una sucesión trivial 0, 0, 0, … o a₁, 0, 0, 0, …

Tipos de progresiones geométricas

La monotonía de una sucesión geométrica (si crece, decrece, alterna o se mantiene constante) depende de la interacción entre dos valores: el primer término a₁ y la razón común r. La razón determina la dirección y el ritmo del cambio, mientras que el primer término establece el punto de partida. Esta combinación da lugar a varios comportamientos característicos que se clasifican de la siguiente manera.

Progresión creciente

Una progresión geométrica es creciente cuando cada término es mayor o igual que el anterior (a_n+1 ≥ a_n). Este comportamiento se manifiesta en dos situaciones principales, dependiendo del signo del primer término:

• Si la razón es mayor que 1 (r > 1) y el primer término es positivo (a₁ > 0), la sucesión es estrictamente creciente. Por ejemplo: 4, 12, 36, 108, … con r = 3.
• Si la razón está comprendida entre 0 y 1 (0 < r < 1) y el primer término es negativo (a₁ < 0), la sucesión también es creciente, ya que los términos, aunque negativos, se acercan a cero. Por ejemplo: -16, -8, -4, -2, … con r = 0,5.

Progresión decreciente

Una sucesión geométrica es decreciente cuando cada término es menor o igual que el anterior (a_n+1 ≤ a_n). Al igual que en el caso creciente, existen dos configuraciones posibles:

• Si la razón está entre 0 y 1 (0 < r < 1) y el primer término es positivo (a₁ > 0), la sucesión es estrictamente decreciente. Un ejemplo es la progresión 1, 1/2, 1/4, 1/8, 1/16, … con r = 1/2.
• Si la razón es mayor que 1 (r > 1) y el primer término es negativo (a₁ < 0), la progresión también es decreciente. Por ejemplo: -2, -6, -18, -54, … con r = 3.

Cuando el valor absoluto de la razón es menor que 1 (|r| < 1), los términos de la progresión, ya sean positivos o negativos, se acercan cada vez más a cero; decimos que la sucesión converge a cero.

Progresión alternante

Una progresión es alternante cuando los términos consecutivos tienen signos opuestos. Esto ocurre cuando la razón común es un número negativo (r < 0), pues la multiplicación por un valor negativo en cada paso invierte sistemáticamente el signo del término anterior.

Por ejemplo, en la sucesión 5, -10, 20, -40, … con r = -2, los términos alternan entre positivo y negativo. El valor absoluto de los términos puede ser creciente (si |r| > 1) o decreciente (si |r| < 1).

Progresión constante

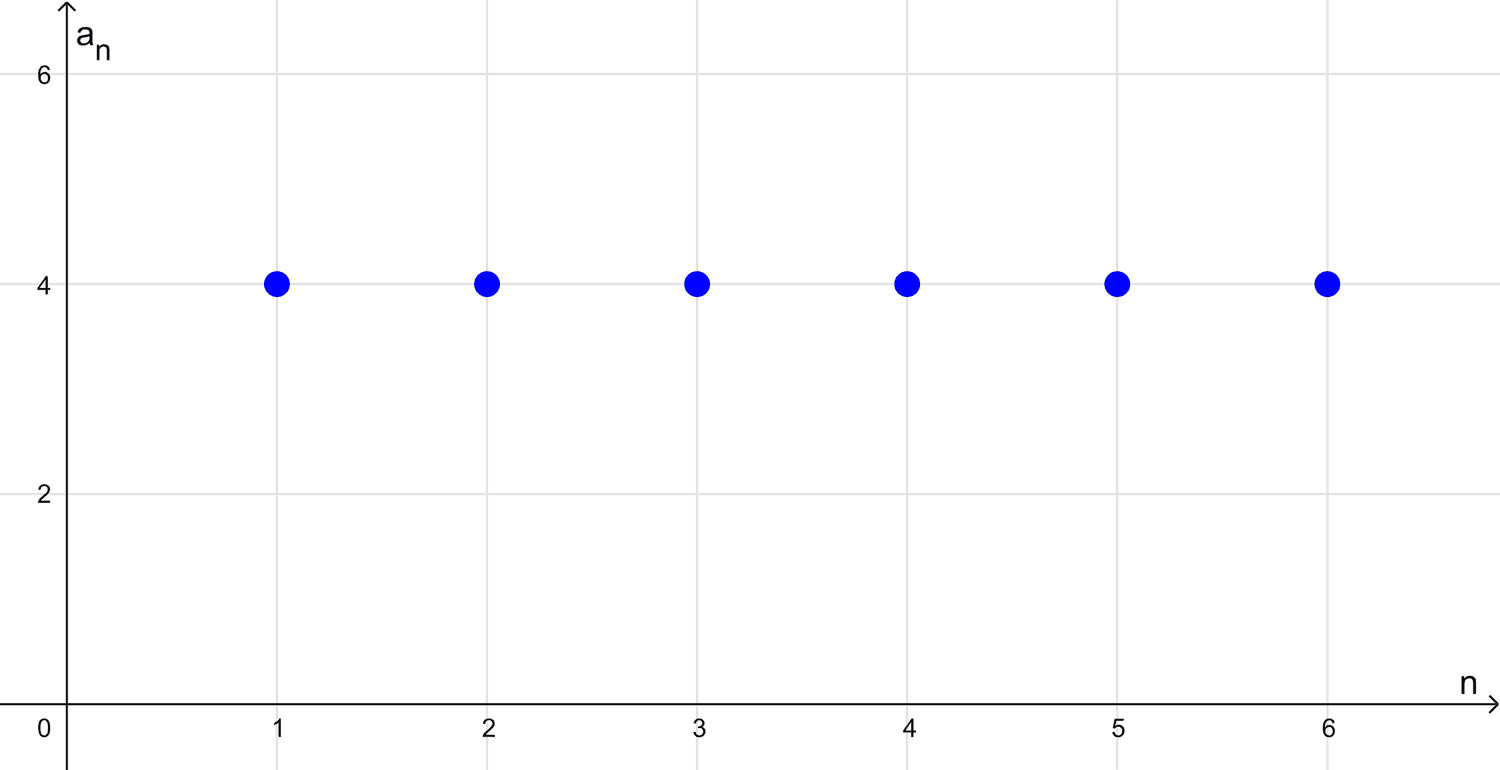
Una progresión geométrica es constante cuando todos sus términos son iguales (a_n+1 = a_n). Este es un caso especial que se presenta cuando la razón es exactamente 1 (r = 1), independientemente del valor del primer término. Ejemplo: 4, 4, 4, 4, …

En la siguiente tabla se resumen los comportamientos.

Primer término	Razón	Monotonía
a1 > 0	r > 1	creciente
	0 < r < 1	decreciente
a1 < 0	r > 1	decreciente
	0 < r < 1	creciente
Cualquier a1 ≠ 0	r = 1	constante
	r < 0	alternada

Fórmula del término general

Calcular un término específico de una progresión geométrica, como el centésimo, mediante la aplicación repetida de la razón sería un proceso extremadamente laborioso. Para resolver este problema, utilizamos una fórmula explícita que permite obtener directamente el valor de cualquier término conociendo solo su posición en la secuencia, el primer término y la razón.

El exponente n - 1 indica cuántas veces se ha aplicado la multiplicación por r para pasar del primer término a₁ al término en la posición n. Por ejemplo, para el cuarto término (n = 4), el exponente es 3, lo que corresponde a a₁ ⋅ r ⋅ r ⋅ r = a₁ ⋅ r³.

Existe una fórmula alternativa que permite calcular el enésimo término a partir de cualquier término y la razón común. Si se conoce el valor de un término a_k y la razón común r, el término general a_n se puede expresar como:

a_n = a_k ⋅ r^n-k

En esta fórmula:

• a_k es el valor de un término conocido en la posición k.
• r es la razón común.
• n es la posición del término que se desea calcular.
• k es la posición del término conocido.

A continuación veremos ejemplos usando ambas fórmulas.

Ejemplo 1

Hallar el quinto término de una progresión geométrica sabiendo que el primer término es 2 y la razón es 3.

Solución

Conocemos directamente el primer término a₁ = 2 y la razón r = 3. La fórmula general de esta progresión es, por lo tanto, a_n = 2 ⋅ 3^n-1. Para hallar el quinto término, simplemente evaluamos esta expresión para n = 5:

\(a_5=2 \cdot 3^{\,5-1}=2 \cdot 3^4=2 \cdot 81=162\)

Así, el quinto término es 162.

Ejemplo 2

Hallar el octavo término de una progresión geométrica cuyos primeros términos son 3, 6, 12, …

Solución

Primero determinamos la razón común dividiendo dos términos consecutivos: r = 6 / 3 = 2. Con el primer término a₁ = 3, la fórmula general que define la sucesión es a_n = 3 ⋅ 2^n-1. Utilizamos esta regla para calcular el octavo término:

\(a_8=3 \cdot 2^{8-1}=3 \cdot 2^7=3 \cdot 128=384\)

El octavo elemento de esta secuencia es 384.

Ejemplo 3

Determinar la razón y el décimo término de una progresión geométrica donde el primer término es 0,001 y el segundo término es 0,01.

Solución

Calculamos la razón común: r = 0,01 / 0,001 = 10. La regla general para cualquier término es entonces a_n = 0,001 ⋅ 10^n-1. Aplicamos esta fórmula para obtener el décimo término:

\(a_{10}=0,001 \cdot 10^{10-1}=0,001 \cdot 10^9=0,001 \cdot 1\,000\,000\,000=1\,000\,000\)

La razón es 10 y el décimo término, usando la fórmula general, es 1 000 000.

Ejemplo 4

El primer término de una progresión geométrica es 3 y el sexto término es 729. Hallar su fórmula general.

Solución

Conocemos a₁ = 3 y a₆ = 729. Para hallar la razón, usamos la relación para el sexto término:

\(a_6=3 ⋅ r^5=729 \)

Despejamos:

\(r^{5}=\dfrac{729}{3}=243 → r=\sqrt[5]{243}=3\)

Por lo tanto, la fórmula del término n-ésimo es a_n = 3 ⋅ 3^n-1, que simplificamos como a_n = 3ⁿ.

Ejemplo 5

Hallar el primer término de una progresión geométrica si el séptimo término es 320 y la razón es 2.

Solución

Sabemos que a₇ = 320 y r = 2. La fórmula general tiene la forma a_n = a₁ ⋅ 2^n-1. Usamos la información del séptimo término para despejar a₁:

\(320=a_1 \cdot 2^{7-1} → 320=a_1 \cdot 64 → a_1=\dfrac{320}{64}=5\)

La fórmula general queda definida como a_n = 5 ⋅ 2^n-1. Reemplazando n por 1, obtenemos que el primer término es 5.

Otra forma de resolver este ejercicio es emplear la fórmula alternativa que relaciona dos términos cualesquiera. Conocemos el séptimo término a₇ = 320 y la razón r = 2. Para hallar el primer término, que se encuentra en la posición k = 1, podemos plantear la relación desde el término conocido a₇:

\(a_1=a_7 \cdot r^{1-7}=320 \cdot 2^{-6}=320 \cdot \dfrac{1}{64}=5\)

Como podemos observar, aplicando esta fórmula alternativa llegamos al mismo resultado: el primer término es 5.

Ejemplo 6

Si en una progresión geométrica el noveno término es igual a 5 y la razón es 1/2, ¿cuál es el valor del primer término?

Solución

La sucesión sigue la regla general a_n = a₁ ⋅ (1/2)^n-1. Sustituimos los datos del noveno término para encontrar el primero:

\(5=a_1 \cdot \left(\dfrac{1}{2}\right)^{9-1}→5=a_1 \cdot \dfrac{1}{256}→a_1=5 \cdot 256=1280\)

Así, la expresión algebraica de la progresión es a_n = 1280 ⋅ (1/2)^n-1 y el primer término es 1280.

Demostración de la fórmula general

Para comprender cómo surge la fórmula explícita a_n = a₁ ⋅ r^n-1, analicemos el patrón que se genera al construir los primeros términos de la sucesión a partir del primer término a₁ y la razón común r.

Partimos del primer término:

\(a_1=a_1\)

Para obtener el segundo término, multiplicamos el primero por la razón r:

\(a_2=a_1 \cdot r\)

El tercer término se obtiene multiplicando el segundo por r:

\(a_3=a_2 \cdot r=(a_1 \cdot r) \cdot r=a_1 \cdot r^2\)

Continuamos con el cuarto término:

\(a_4=a_3 \cdot r=(a_1 \cdot r^2) \cdot r=a_1 \cdot r^3\)

Si observamos atentamente este patrón, notamos que el exponente de la razón r es siempre una unidad menor que la posición del término. Es decir:

• Para el término 1, el exponente es 0.
• Para el término 2, el exponente es 1.
• Para el término 3, el exponente es 2.
• Para el término 4, el exponente es 3.

Generalizando este patrón, para el término n-ésimo, el exponente de r será n - 1. Por lo tanto, la expresión general queda establecida intuitivamente como:

\(a_n=a_1 \cdot r^{n-1}\)

Para una verificación formal de que este patrón se cumple para todos los números naturales n, podemos emplear el método de inducción matemática.

Paso base (n = 1): Para el primer término, la fórmula propuesta es:

\(a_1=a_1 \cdot r^{1-1}=a_1 \cdot r^0=a_1 \cdot 1=a_1\)

Se cumple trivialmente.

Paso inductivo: Supongamos que la fórmula es válida para un término k cualquiera; es decir, suponemos como hipótesis de inducción que:

\(a_k=a_1 \cdot r^{k-1}\)

Ahora, debemos demostrar que la fórmula también se cumple para el término k + 1. Por la definición recursiva de una progresión geométrica, sabemos que:

\(a_{k+1}=a_k \cdot r\)

Sustituimos nuestra hipótesis de inducción en esta ecuación:

\(a_{k+1}=(a_1 \cdot r^{k-1}) \cdot r\)

\(a_{k+1}=a_1 \cdot r^{(k-1)+1}\)

\(a_{k+1}=a_1 \cdot r^{k}\)

\(a_{k+1}=a_1 \cdot r^{(k+1)-1}\)

Este último resultado muestra que la fórmula sí se cumple para el término k + 1. Habiendo verificado el paso base y el paso inductivo, concluimos que la fórmula del término general

\(a_n=a_1 \cdot r^{n-1}\)

es válida para todo número natural n ≥ 1.

Suma de términos

En muchas aplicaciones prácticas, no solo es importante conocer un término específico de una progresión geométrica, sino también el resultado de sumar varios de sus términos consecutivos.

Esta sumatoria, conocida como serie geométrica, puede calcularse término a término, pero este método se vuelve muy engorroso cuando el número de términos es grande. Afortunadamente, existe una fórmula que nos permite hallar la suma de los primeros n términos de manera directa.

Suma de los primeros n términos

Ejemplo 1

Calcular la suma de los primeros diez términos de la secuencia 1, 3, 9, 27, …

Solución

Primero identificamos los elementos de la progresión. El primer término es a₁ = 1. La razón común es r = 3 / 1 = 3. Queremos calcular la suma de los primeros diez términos (n = 10). Aplicamos directamente la fórmula de la suma:

\(S_{10}=1 \cdot \dfrac{1-3^{10}}{1-3}=\dfrac{1-59049}{-2}=\dfrac{-59048}{-2}=29524\)

Por lo tanto, la suma de los primeros diez términos de esta progresión geométrica es 29 524.

Ejemplo 2

El tercer término de una progresión geométrica es 12 y la razón es 2. Calcular la suma de los primeros cinco términos.

Solución

Conocemos un término no inicial, a₃ = 12, y la razón r = 2. Para usar la fórmula de la suma, primero necesitamos hallar el primer término a₁. Usamos la relación a₃ = a₁ ⋅ r² para despejarlo:

\(12=a_1 \cdot 2^2→12=4a_1→a_1=3\)

Ahora, con a₁ = 3, r = 2 y n = 5, calculamos la suma solicitada:

\(S_5=3 \cdot \dfrac{1-2^{5}}{1-2}=3 \cdot \dfrac{1-32}{-1}=3 \cdot \dfrac{-31}{-1}=3 \cdot 31=93\)

La suma de los primeros cinco términos de esta progresión es 93.

Demostración de la fórmula de la suma

Para deducir la fórmula de la suma de los primeros n términos de una sucesión geométrica, partimos de su definición. La suma S_n se escribe como:

\(S_n=a_1+a_1 r+a_1 r^2+\ldots+a_1 r^{n-1}\)

Un método ingenioso para simplificar esta expresión consiste en multiplicar ambos lados de la igualdad por la razón común r:

\(r S_n=a_1 r+a_1 r^2+a_1 r^3+\ldots+a_1 r^{n}\)

Ahora, restamos esta segunda ecuación de la primera, miembro a miembro (S_n - rS_n). Observemos que al hacer esta resta, todos los términos intermedios se cancelan, ya que a₁ r - a₁ r = 0, a₁ r² - a₁ r² = 0, y así sucesivamente, hasta el penúltimo término de S_n. El resultado de la resta es:

\(S_n-r S_n=a_1-a_1 r^{n}\)

En el lado izquierdo podemos factorizar S_n, obteniendo S_n (1 - r). En el lado derecho, factorizamos a₁. La ecuación queda:

\(S_n (1-r)=a_1 (1-r^{n})\)

Para despejar S_n, dividimos ambos lados entre (1 - r). Esta operación solo es válida si el divisor es distinto de cero. Por lo tanto, esta fórmula solo es aplicable cuando la razón r es diferente de 1. Asumiendo r ≠ 1, despejamos S_n y llegamos a la fórmula final:

\(S_n=a_1 \cdot \dfrac{1-r^{n}}{1-r}\)

Si r = 1, la progresión es constante (todos los términos son iguales a a₁) y su suma se calcula simplemente como S_n = n ⋅ a₁.

Suma infinita

Intuitivamente, podría pensarse que al sumar cada vez más términos de una progresión geométrica, el resultado siempre crecerá indefinidamente (tenderá a infinito) o decrecerá sin límite (tenderá a menos infinito). Si bien esto ocurre en muchos casos (como en la sucesión 2, 4, 8, 16, … donde la suma crece rápidamente), existe un escenario especial en el que la suma de un número infinito de términos se aproxima a un valor fijo y finito.

Este comportamiento sucede cuando el valor absoluto de la razón común es menor que 1, es decir, cuando -1 < r < 1, provoncando una sucesión decreciente. En tales progresiones, cada nuevo término añadido es más pequeño en valor absoluto que el anterior, y su contribución a la suma total se vuelve insignificante a medida que avanzamos. Matemáticamente, decimos que la serie geométrica es convergente y que su suma infinita existe.

Esta expresión se obtiene al considerar el límite de la fórmula de la suma finita S_n cuando el número de términos n tiende a infinito. Dado que |r| < 1, la potencia rⁿ se aproxima a cero cuando n crece indefinidamente \((\lim_{n \to ∞} r^{n}=0).\) Al sustituir este límite en la fórmula finita, el término rⁿ desaparece, resultando en la fórmula compacta mostrada anteriormente. Si |r| ≥ 1, la serie no converge a un número finito y decimos que la suma infinita no existe (no es un número finito).

Ejemplo

Analizar si la progresión 1, 1/2, 1/4, 1/8, 1/16, … tiene suma infinita y cuál es su valor.

Solución

La suma que queremos analizar es la de infinitos términos de esta progresión con fracciones:

\(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\ldots\)

Obtenemos el primer término a₁ = 1 y la razón común \(r=\dfrac{1/2}{1}=\dfrac{1}{2}.\)

Si realizamos la suma manual de los primeros diez términos, utilizando la fórmula para la suma finita o sumando directamente, observamos una tendencia clara. La suma de los primeros diez términos es:

\(S_{10}=1 \cdot \dfrac{1-(1/2)^{10}}{1-1/2}=\dfrac{1-1/1024}{1/2}=2 \cdot \left(1-\dfrac{1}{1024}\right)=2-\dfrac{2}{1024} ≈ 1,998\)

Vemos que esta suma parcial ya se acerca mucho al valor 2, y si sumáramos más términos, la diferencia sería cada vez menor.

Para determinar si la suma infinita existe, verificamos la condición de convergencia. El valor absoluto de la razón es |r| = |1/2| = 0,5, que es estrictamente menor que 1. Por lo tanto, se cumple la condición |r| < 1 y podemos afirmar que la serie geométrica infinita es convergente.

Aplicamos la fórmula para la suma infinita de una progresión geométrica con a₁ = 1 y r = 1/2:

\(S_{∞}=\dfrac{a_1}{1-r}=\dfrac{1}{1-1/2}=\dfrac{1}{1/2}=2\)

Concluimos que la suma de todos los términos de la progresión geométrica infinita dada existe y su valor exacto es 2.

Aplicaciones

La esencia de las progresiones geométricas es modelar fenómenos de crecimiento o decrecimiento multiplicativo, también llamado exponencial. A diferencia del crecimiento aditivo y constante característico de las progresiones aritméticas, estas sucesiones describen procesos donde el cambio en cada paso es proporcional al valor actual.

Encontramos este patrón con frecuencia en contextos económicos y financieros, donde el valor del dinero, las inversiones y los préstamos evolucionan de forma exponencial debido a la capitalización de intereses.

Interés compuesto

El interés compuesto es la aplicación financiera más directa de una progresión geométrica. Se diferencia del interés simple, donde los intereses generados no se reinvierten y la ganancia por periodo es constante (modelo aritmético).

En el interés compuesto, los intereses de cada periodo se añaden al capital inicial para formar un nuevo capital, sobre el cual se calcularán los intereses del siguiente periodo. Esto genera un crecimiento exponencial del capital a lo largo del tiempo.

La fórmula que calcula el capital final C_f después de n periodos de capitalización es:

\(C_f=C_0 \cdot (1+i)^{n}\)

donde C₀ es el capital inicial, i es la tasa de interés por periodo (expresada en decimal) y n es el número total de periodos. Reconociendo la analogía, C₀ es el primer término, la razón común es r = (1 + i), y n es la posición del término.

Ejemplo

Juan deposita $1000 en una cuenta de ahorros que ofrece una tasa de interés compuesto anual del 5%. ¿Cuál será el monto total acumulado en la cuenta después de 8 años?

Solución

Identificamos los elementos de la fórmula. El capital inicial es C₀ = 1000. La tasa de interés anual es i = 5% = 0,05. El número de periodos (años) es n = 8. Aplicamos la fórmula del interés compuesto, que es la fórmula del término general de una progresión geométrica:

\(C_f=1000 \cdot (1+0,05)^{8}=1000 \cdot (1,05)^{8}≈1477,46\)

Por lo tanto, después de 8 años, Juan tendrá aproximadamente $1477,46 en su cuenta. Este monto es superior al que obtendría con interés simple, el cual sería 1000 + 1000 ⋅ 0,05 ⋅ 8 = 1400.

Depreciación de activos

El valor de un activo, como una máquina, un vehículo o un equipo tecnológico, no permanece constante con el tiempo, sino que va perdiendo valor. Uno de los modelos más utilizados para cuantificar esta pérdida es la depreciación por porcentaje constante, también llamada depreciación geométrica.

En este modelo, el activo pierde cada año un porcentaje fijo de su valor actual, no de su valor original. Este comportamiento es el de una progresión geométrica decreciente, donde la razón común r es un número positivo menor que 1 (0 < r < 1).

Si denotamos V₀ como el valor inicial del activo, p como el porcentaje anual de depreciación (expresado en decimal) y n como el número de años transcurridos, la razón común es r = 1 - p. El valor del activo después de n años, V_n, viene dado por la fórmula del término general:

\(V_n=V_0 \cdot (1-p)^{n} \quad \text{o, equivalentemente,} \quad V_n=V_0 \cdot r^{n}\)

Ejemplo

Un coche nuevo se compra por un valor de $20 000. Se estima que su valor se deprecia a una tasa constante del 15% anual. ¿Cuál será el valor aproximado del vehículo después de 6 años?

Solución

Identificamos los datos del problema. El valor inicial es V₀ = 20 000. La tasa de depreciación anual es p = 15% = 0,15. Por lo tanto, la razón de la progresión geométrica que modela su valor es r = 1 - 0,15 = 0,85. Queremos hallar el valor después de n = 6 años.

Aplicamos la fórmula de depreciación geométrica, que es análoga a la del término general:

\(V_6=20000 \cdot (0,85)^{6}≈7542,99\)

Podemos concluir que, siguiendo este modelo de depreciación, el valor aproximado del coche después de 6 años será de $7542,99.

Propiedades

Además de la propiedades de la razón constante y las fórmulas para el término general y la suma, las progresiones geométricas poseen otras propiedades algebraicas y estructurales que son muy útiles para la resolución de problemas.

Producto de términos equidistantes

En una progresión geométrica finita de n términos, el producto de dos términos que equidistan de los extremos es constante e igual al producto del primer y último término. Es decir, si a₁, a₂, …, a_n forman una PG, entonces:

\(a_1\cdot a_n=a_2\cdot a_{n-1}=a_3\cdot a_{n-2}=\ldots\)

Ejemplo

Consideremos la progresión 2, 6, 18, 54, 162. El producto de los extremos es 2 ⋅ 162 = 324. El producto de los términos equidistantes siguientes es 6 ⋅ 54 = 324, confirmando la propiedad.

Demostración

Sea \(a_k\) un término cualquiera y \(a_{n-k+1}\) su equidistante. Usando la fórmula general, tenemos \(a_k=a_1\cdot r^{k-1}\) y \(a_{n-k+1}=a_1\cdot r^{n-k}.\) Su producto es:

\(a_k\cdot a_{n-k+1}=(a_1\cdot r^{k-1})\cdot (a_1\cdot r^{n-k})=a_1^2\cdot r^{n-1}\)

Este resultado no depende de \(k,\) ya que \(a_1^2\cdot r^{n-1}=(a_1)\cdot (a_1\cdot r^{n-1})=a_1\cdot a_n.\) Por lo tanto, el producto de cualquier par de términos equidistantes es siempre \(a_1\cdot a_n.\)

Producto de los primeros n términos

El producto P_n de los primeros n términos de una progresión geométrica se puede calcular elevando el producto del primer y último término a la mitad del número de términos. Una fórmula directa es:

\(P_n=(a_1\cdot a_n)^{n/2}\)

Si n es impar, la fórmula sigue siendo válida si se interpreta la potencia fraccionaria correctamente.

Ejemplo

Para la PG 1, 3, 9, 27, 81 (\(a_1=1, a_5=81, n=5\)), el producto es

\(P_5=(1\cdot 81)^{5/2}=81^{2,5}\)

Notamos que \(81^{2}\cdot 81^{0,5}=6561\cdot 9=59049,\) que coincide con \(1\cdot 3\cdot 9\cdot 27\cdot 81.\)

Demostración

Partimos de \(P_n=a_1\cdot a_2\cdot \ldots\cdot a_n.\) Sustituyendo cada término por su fórmula general \(a_k=a_1 r^{k-1},\) obtenemos:

\(P_n=a_1\cdot (a_1 r)\cdot (a_1 r^2)\cdot \ldots\cdot (a_1 r^{n-1})=a_1^{n}\cdot r^{0+1+2+\ldots+(n-1)}\)

La suma de los exponentes de \(r\) es

\(0+1+2+\ldots+(n-1)=\dfrac{n(n-1)}{2}\)

Por lo tanto, \(P_n=a_1^{n}\cdot r^{n(n-1)/2}.\) Observamos que

\(a_1\cdot a_n=a_1\cdot (a_1 r^{n-1})=a_1^2\cdot r^{n-1}\)

Si elevamos este producto a \(n/2:\)

\((a_1\cdot a_n)^{n/2}=(a_1^2\cdot r^{n-1})^{n/2}=a_1^{n}\cdot r^{n(n-1)/2}=P_n\)

lo que demuestra la fórmula.

Término central en una PG con número impar de términos

Si una progresión geométrica finita tiene un número impar de términos n, entonces el término central a_c es la media geométrica del primer y el último término. Es decir:

\(a_c=\sqrt{a_1\cdot a_n}\)

Ejemplo

En la PG 4, 12, 36, 108, 324 (\(n=5\)), el término central es \(a_3=36.\) El producto de los extremos es \(4\cdot 324=1296,\) y su raíz cuadrada es \(\sqrt{1296}=36,\) confirmando la propiedad.

Demostración

Sea \(n=2k-1\) (un número impar), de modo que el término central ocupa la posición \(k.\) Su valor es \(a_k=a_1\cdot r^{k-1}.\) El último término es \(a_n=a_1\cdot r^{n-1}=a_1\cdot r^{2k-2}.\)

Calculamos el producto de los extremos:

\(a_1\cdot a_n=a_1^2\cdot r^{2k-2}=(a_1\cdot r^{k-1})^2=(a_k)^2\)

Por lo tanto,

\(a_k=\sqrt{a_1\cdot a_n}\)

que es precisamente la definición de la media geométrica entre \(a_1\) y \(a_n.\)

Relación con los logaritmos

Si tomamos una progresión geométrica cuyos términos son todos positivos y aplicamos la función logaritmo (en cualquier base) a cada uno de sus términos, la sucesión resultante es una progresión aritmética, cuya diferencia común es el logaritmo de la razón (d = log(r)). Este vínculo convierte problemas de multiplicación en problemas de suma.

Ejemplo

Dada la PG 10, 100, 1000, 10000, … con razón r = 10, al aplicar logaritmo en base 10 obtenemos:

log₁₀(10) = 1, log₁₀(100) = 2, log₁₀(1000) = 3,…

que es la progresión aritmética 1, 2, 3, 4,… con diferencia común d = 1.

Demostración

Sea la PG \(a_1, a_2, a_3, \ldots\) con \(a_n=a_1\cdot r^{n-1}\) y \(a_1>0.\) Aplicamos el logaritmo al término general y propiedades de los logaritmos:

\(\log(a_n)=\log(a_1\cdot r^{n-1})=\log(a_1)+(n-1)\log(r)\)

Definiendo \(b_1=\log(a_1)\) y \(d=\log(r),\) la expresión se reescribe como \(\log(a_n)=b_1+(n-1)d.\) Esta es precisamente la fórmula del término general de una progresión aritmética con primer término \(b_1\) y diferencia común \(d=\log(r).\) Por tanto, la secuencia creada es una progresión aritmética.

Resumen de fórmulas

Nombre	Fórmula
Fórmula recursiva	a1 an = an-1 ⋅ r (para n ≥ 2) a1 ≠ 0 y r ≠ 0
Término general	an = a1 ⋅ rn-1
Suma de los primeros n términos	Sn = a1 ⋅ (1 - rn) / (1 - r) (para r ≠ 1) Sn = n ⋅ a1 (para r = 1)
Suma infinita	S∞ = a1 / (1 - r) (solo si |r| < 1)
Producto de los primeros n términos	Pn = (a1 ⋅ an) n/2
Término central (n impar)	ac = √(a1 ⋅ an)

Ejercicios resueltos

Ejercicio 1

Determinar la razón, el término general y la monotonía de las siguientes progresiones geométricas:

1. 5, 15, 45, 135, 405,...
2. 1000, 500, 250, 125, …
3. -2, -4, -8, -16, -32, …
4. 1/3, 2/3, 2, 6, 18, …
5. 3/4, 1/2, 1/3, 2/9, 4/27, …
6. 50; 10; 2; 0,4; 0,08; 0,016, …

Solución

a) 5, 15, 45, 135, 405,...

Calculamos la razón común r dividiendo cualquier término por el anterior:

\(r=\dfrac{15}{5}=3\)

El primer término es a₁ = 5, por lo tanto la fórmula del término general es

\(a_n=a_1 \cdot r^{n-1}=5 \cdot 3^{n-1}\)

Como a₁ > 0 y r > 1, la progresión es estrictamente creciente.

b) 1000, 500, 250, 125,...

La razón es

\(r=\dfrac{500}{1000}=0,5\)

Con a₁ = 1000, el término general se expresa como

\(a_n=1000 \cdot (0,5)^{n-1}\)

Dado que a₁ > 0 y 0 < r < 1, la sucesión es estrictamente decreciente y converge a cero.

c) -2, -4, -8, -16, -32,...

Determinamos la razón:

\(r=\dfrac{-4}{-2}=2\)

El primer término es a₁ = -2, así que

\(a_n=-2 \cdot 2^{n-1}=-2^{n}\)

Aquí a₁ < 0 y r > 1, por lo que la progresión es estrictamente decreciente (los términos son negativos y su valor absoluto crece).

d) \(\dfrac{1}{3}, \dfrac{2}{3}, 2, 6, 18,...\)

Primero hallamos la razón entre los dos primeros términos:

\(r=\dfrac{2/3}{1/3}=2\)

El término general queda

\(a_n=\dfrac{1}{3} \cdot 2^{n-1}\)

Como a₁ > 0 y r > 1, la sucesión es estrictamente creciente.

e) \(\dfrac{3}{4}, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{2}{9}, \dfrac{4}{27},...\)

Calculamos la razón:

\(r=\dfrac{1/2}{3/4}=\dfrac{1}{2}\cdot\dfrac{4}{3}=\dfrac{2}{3}\)

Con \(a_1=\dfrac{3}{4},\) obtenemos

\(a_n=\dfrac{3}{4} \cdot \left(\dfrac{2}{3}\right)^{n-1}\)

Puesto que a₁ > 0 y 0 < r < 1, la progresión es estrictamente decreciente y converge a cero.

f) 50; 10; 2; 0,4; 0,08; 0,016;...

La razón es

\(r=\dfrac{10}{50}=0,2\)

Tomando a₁ = 50, escribimos el término general:

\(a_n=50 \cdot (0,2)^{n-1}\)

Dado que a₁ > 0 y 0 < r < 1, la progresión es estrictamente decreciente y sus términos se acercan a cero.

Ejercicio 2

Obtener el 7° término de la progresión geométrica cuyos segundo y tercer término son 2 y -√2, respectivamente.

Solución

Conocemos a₂ = 2 y a₃ = -√2. Primero hallamos la razón común r dividiendo el tercer término entre el segundo:

\(r=\dfrac{a_3}{a_2}=\dfrac{-\sqrt{2}}{2}=-\dfrac{\sqrt{2}}{2}\)

Para calcular el primer término a₁, usamos la relación a₂ = a₁ ⋅ r:

\(2=a_1 \cdot \left(-\dfrac{\sqrt{2}}{2} \right) → a_1=\dfrac{2}{-\dfrac{\sqrt{2}}{2}}=2 \cdot \left(-\dfrac{2}{\sqrt{2}} \right)=-\dfrac{4}{\sqrt{2}}=-2\sqrt{2}\)

Ahora aplicamos la fórmula del término general a_n = a₁ ⋅ r ^{n - 1} para n = 7:

\(a_7=(-2\sqrt{2}) \cdot \left(-\dfrac{\sqrt{2}}{2} \right)^{6}\)

Calculamos la potencia:

\(\left(-\dfrac{\sqrt{2}}{2} \right)^{6}=\left(\left(-\dfrac{\sqrt{2}}{2} \right)^{2} \right)^{3}=\left(\dfrac{2}{4} \right)^{3}=\left(\dfrac{1}{2} \right)^{3}=\dfrac{1}{8}\)

Entonces:

\(a_7=(-2\sqrt{2}) \cdot \dfrac{1}{8}=-\dfrac{2\sqrt{2}}{8}=-\dfrac{\sqrt{2}}{4}\)

Por lo tanto, el séptimo término es \(-\dfrac{\sqrt{2}}{4}.\)

Ejercicio 3

Cuenta la leyenda que un sabio inventó el ajedrez y se lo presentó a un rey; este último, fascinado, le ofreció cualquier recompensa. El inventor pidió un grano de arroz en la primera casilla del tablero, dos en la segunda, cuatro en la tercera, y así duplicando la cantidad en cada una de las 64 casillas. ¿Cuántos granos de arroz debería entregarle el rey? Si en un kilogramo hay aproximadamente 50 000 granos, ¿a cuántos kilogramos equivalen?

Solución

Identificamos los datos: el primer término de la progresión geométrica es a₁ = 1 y la razón común es r = 2, ya que cada casilla tiene el doble de granos que la anterior. El número de términos es n = 64, correspondiente a las 64 casillas del tablero. Para calcular la cantidad total de granos, que es la suma de todos los términos, utilizamos la fórmula de la suma de los primeros n términos de una progresión geométrica:

\(S_n=a_1 \cdot \dfrac{1-r^{n}}{1-r}\)

Sustituimos los valores conocidos:

\(S_{64}=1 \cdot \dfrac{1-2^{64}}{1-2}=\dfrac{1-2^{64}}{-1}=2^{64}-1\)

Calculamos 2⁶⁴ usando potencias sucesivas:

\(2^{10}=1024,\quad 2^{20}=(2^{10})^2=1024^2=1 048 576,\quad 2^{40}=(2^{20})^2 ≈ 1\,099\, 511\, 627\, 776\)

\(2^{64}=2^{40} \cdot 2^{24}=1\, 099\, 511\, 627\, 776 \cdot 16\, 777\, 216\)

Realizando la multiplicación obtenemos:

\(2^{64}=18\,446\,744\,073\,709\,551\,616\)

Por lo tanto:

\(S_{64}=18\, 446\, 744\, 073\, 709\, 551\, 616-1=18\, 446\, 744\, 073\, 709\, 551\, 615\)

El rey debería entregar 18 446 744 073 709 551 615 granos de arroz (más de 18 trillones).

Ahora convertimos esta cantidad a kilogramos. Dado que en un kilogramo hay aproximadamente 50 000 granos, dividimos el total de granos entre 50 000:

\(\text{Kilogramos}=\dfrac{18\, 446\, 744\, 073\, 709\, 551\, 615}{50\, 000}=368\, 934\, 881\, 474\, 191,0323\)

Es decir, aproximadamente 368 934 881 474 191 kilogramos (unos 368 billones de kilogramos).

Nota: la producción mundial de arroz se estima en 780 mil millones de kilogramos anuales en la actualidad. Esto significa que para cubrir la cantidad de arroz, el rey debería entregar la producción mundial completa de 473 años.

Ejercicio 4

María quiere comprarse una computadora y ahorra $300 el primer mes y cada mes ahorra el doble de lo ahorrado el mes anterior, ¿cuánto tiene al noveno mes?

Solución

Interpretamos que el problema pregunta por el total ahorrado después de nueve meses, es decir, la suma de lo ahorrado cada mes. Los ahorros mensuales forman una progresión geométrica con primer término a₁ = 300 y razón r = 2. Queremos la suma de los primeros nueve términos (n = 9).

Aplicamos la fórmula de la suma:

\(S_n=a_1 \cdot \dfrac{1-r^{n}}{1-r}\)

\(S_9=300 \cdot \dfrac{1-2^{9}}{1-2}=300 \cdot \dfrac{1-512}{-1}=300 \cdot \dfrac{-511}{-1}=300 \cdot 511=153 300\)

Así, al noveno mes María tiene un total de $153 300 ahorrados.

Ejercicio 5

Calcular la suma de los diez primeros términos de la sucesión 2, - 2, 2, - 2, …

Solución

Reconocemos que se trata de una progresión geométrica con primer término a₁ = 2 y razón común r = -1, pues cada término se obtiene multiplicando el anterior por -1. Queremos la suma de los primeros diez términos (n = 10).

Aplicamos la fórmula de la suma de los primeros n términos de una PG:

\(S_n=a_1\cdot \dfrac{1-r^{n}}{1-r}\)

Sustituimos a₁ = 2, r = -1, n = 10:

\(S_{10}=2\cdot \dfrac{1-(-1)^{10}}{1-(-1)}=2\cdot \dfrac{1-1}{1+1}=2\cdot \dfrac{0}{2}=0\)

Por lo tanto, la suma de los primeros diez términos es 0.

Ejercicio 6

Encontrar la suma de los primeros nueve términos de la sucesión geométrica 1; 0,7; 0,49; 0,343; …

Solución

Identificamos el primer término a₁ = 1 y calculamos la razón común dividiendo el segundo término entre el primero:

\(r=\dfrac{0,7}{1}=0,7\)

Queremos la suma de los primeros nueve términos (n = 9). Usamos la fórmula de la suma:

\(S_9=1\cdot \dfrac{1-(0,7)^{9}}{1-0,7}=\dfrac{1-0,7^9}{0,3}\)

Calculamos:

\(S_9=\dfrac{1-0,040353607}{0,3}=\dfrac{0,959646393}{0,3}=3,19882131\)

Redondeando a un valor razonable, la suma de los primeros nueve términos es aproximadamente 3,199.

Ejercicio 7

En una progresión geométrica se conoce a₃ = 8 y a₆ = 512, determine el término a₈ y la suma S₈.

Solución

Usamos la relación entre términos de una PG: a₆ = a₃ ⋅ r ³, pues desde el tercer al sexto término hay 6 - 3 = 3 pasos. Sustituimos:

\(512=8\cdot r^{3}→r^{3}=\dfrac{512}{8}=64→r=\sqrt[3]{64}=4\)

Ahora hallamos el primer término a₁ usando a₃ = a₁ ⋅ r ²:

\(8=a_1\cdot 4^{2}=a_1\cdot 16→a_1=\dfrac{8}{16}=0,5\)

Calculamos el octavo término con la fórmula general a_n = a₁ ⋅ r ^n-1:

\(a_8=0,5\cdot 4^{7}=0,5\cdot 16384=8192\)

Ahora determinamos la suma de los primeros ocho términos:

\(S_8=a_1\cdot \dfrac{1-r^{8}}{1-r}=0,5\cdot \dfrac{1-4^8}{1-4}=0,5\cdot \dfrac{1-65536}{-3}\)

Resolviendo:

\(S_8=0,5\cdot \dfrac{-65535}{-3}=0,5\cdot 21845=10922,5\)

Por lo tanto, a₈ = 8192 y S₈ = 10922,5.

Ejercicio 8

En una PG a₅ = 1/6 y r = 3/2. Determinar a₁ y S₅.

Solución

Usamos la fórmula del término general a_n = a₁ ⋅ r ^n-1 para n = 5:

\(\dfrac{1}{6}=a_1\cdot \left(\dfrac{3}{2}\right)^{4}→a_1=\dfrac{1}{6}\cdot \dfrac{16}{81}=\dfrac{16}{486}=\dfrac{8}{243}\)

Ahora calculamos la suma de los primeros cinco términos:

\(S_5=a_1\cdot \dfrac{1-r^{5}}{1-r}=\dfrac{8}{243}\cdot \dfrac{1-\left(\dfrac{3}{2}\right)^5}{1-\dfrac{3}{2}}\)

Calculamos:

\(S_5=\dfrac{8}{243}\cdot \dfrac{1-\dfrac{243}{32}}{1-\dfrac{3}{2}}=\dfrac{8}{243}\cdot \dfrac{\dfrac{32-243}{32}}{\dfrac{-1}{2}}=\dfrac{8}{243}\cdot \dfrac{\dfrac{-211}{32}}{\dfrac{-1}{2}}\)

Simplificamos la división de fracciones:

\(S_5=\dfrac{8}{243}\cdot \left(\dfrac{-211}{32}\cdot \dfrac{2}{-1}\right)=\dfrac{8}{243}\cdot \left(\dfrac{-211}{16}\cdot (-1)\right)=\dfrac{8}{243}\cdot \dfrac{211}{16}=\dfrac{1}{243}\cdot \dfrac{211}{2}=\dfrac{211}{486}\)

Por lo tanto, a₁ = 8/243 y S₅ = 211/486.

Ejercicio 9

Pedro compró un terreno a pagar en 15 años de este modo: $1 el primer año, $3 el segundo año, $9 el tercer año, y así sucesivamente. ¿Cuál es el importe del terreno?

Solución

Observamos que los pagos anuales siguen una progresión geométrica. El primer término es a₁ = 1 y la razón común es r = 3, ya que cada año el pago se triplica respecto al anterior. Como los pagos se realizan durante 15 años, necesitamos hallar la suma de los primeros 15 términos de esta progresión. Aplicamos la fórmula de la suma de los primeros n términos de una progresión geométrica:

\(S_n=a_1\cdot \dfrac{1-r^n}{1-r}\)

Sustituimos a₁ = 1, r = 3 y n = 15:

\(S_{15}=1\cdot \dfrac{1-3^{15}}{1-3}=\dfrac{1-3^{15}}{-2}\)

Desarrollando la potencia y resolviendo:

\(S_{15}=\dfrac{1-14 348 907}{-2}=\dfrac{-14 348 906}{-2}=7\, 174\, 453\)

Por lo tanto, el importe total del terreno es de $7.174.453.

Ejercicio 10

Un hombre ahorra cada año los 2/3 de lo que ahorró el año anterior. Ahorró en el quinto año $160, ¿cuánto ha ahorrado en los cinco años?

Solución

El ahorro anual sigue una progresión geométrica decreciente. Conocemos el quinto término a₅ = 160 y la razón común r = 2/3. Primero determinamos el primer término a₁ usando la fórmula del término general a_n = a₁ ⋅ r^n-1. Para n = 5:

\(160=a_1\cdot \left(\dfrac{2}{3}\right)^{4}\)

Despejamos a₁:

\(a_1=160\cdot \dfrac{81}{16}=10\cdot 81=810\)

Ahora hallamos la suma de los primeros cinco términos con la fórmula de la suma:

\(S_5=a_1\cdot \dfrac{1-r^5}{1-r}\)

Sustituimos a₁ = 810, r = 2/3 y calculamos \(r^5=\left(\dfrac{2}{3}\right)^5=\dfrac{32}{243}:\)

\(S_5=810\cdot \dfrac{1-\dfrac{32}{243}}{1-\dfrac{2}{3}}=810\cdot \dfrac{\dfrac{243-32}{243}}{\dfrac{1}{3}}=810\cdot \dfrac{\dfrac{211}{243}}{\dfrac{1}{3}}=810\cdot \dfrac{211}{243}\cdot 3\)

\(=810\cdot \dfrac{211}{81}=10\cdot 211=2110\)

Por tanto, el total ahorrado en los cinco años es $2 110.

Ejercicio 11

Katty realizó un depósito de $1500 en una cuenta que paga 1,2% de interés mensual, determinar la cantidad en la cuenta después de 2 años.

Solución

Este es un problema de interés compuesto, que se modela con una progresión geométrica. El capital inicial es C₀ = 1500, la tasa de interés mensual es i = 1,2% = 0,012, y el tiempo total es de 2 años, es decir, n = 24 meses. Usamos la fórmula del capital final en interés compuesto, que es análoga a la del término general de una progresión geométrica:

\(C_f=C_0\cdot (1+i)^{n}\)

Sustituimos los valores:

\(C_f=1500\cdot (1+0,012)^{24}=1500\cdot (1,012)^{24}≈1500\cdot 1,331473=1997,209\)

Redondeando a dos decimales, la cantidad en la cuenta después de 2 años será aproximadamente $1997,21.

Ejercicio 12

Un cultivo contiene inicialmente 10000 bacterias y aumenta en 20% cada hora.

a) Encuentre una fórmula para el número B(t) de bacterias presentes después de t horas.

b) ¿Cuántas bacterias hay en el cultivo al término de 10 horas?

Solución

a) El crecimiento es porcentual constante, lo cual corresponde a una progresión geométrica. La población inicial es B(0) = 10 000 y la tasa de crecimiento por hora es del 20%, es decir, cada hora la población se multiplica por 1 + 0,20 = 1,2. Después de t horas, la población habrá sido multiplicada t veces por 1,2. Por tanto, la fórmula es:

\(B(t)=10 000\cdot (1,2)^{t}\)

b) Para t = 10 horas, calculamos:

\(B(10)=10 000\cdot (1,2)^{10}≈10 000\cdot 6,1917=61\, 917,36\)

Redondeando al número entero más cercano, al término de 10 horas habrá aproximadamente 61 917 bacterias.

Ejercicio 13

Se deja caer una pelota desde una altura de 10 metros. Si rebota la mitad de la distancia en cada caída, calcula la distancia total que recorre la pelota antes de detenerse.

Solución

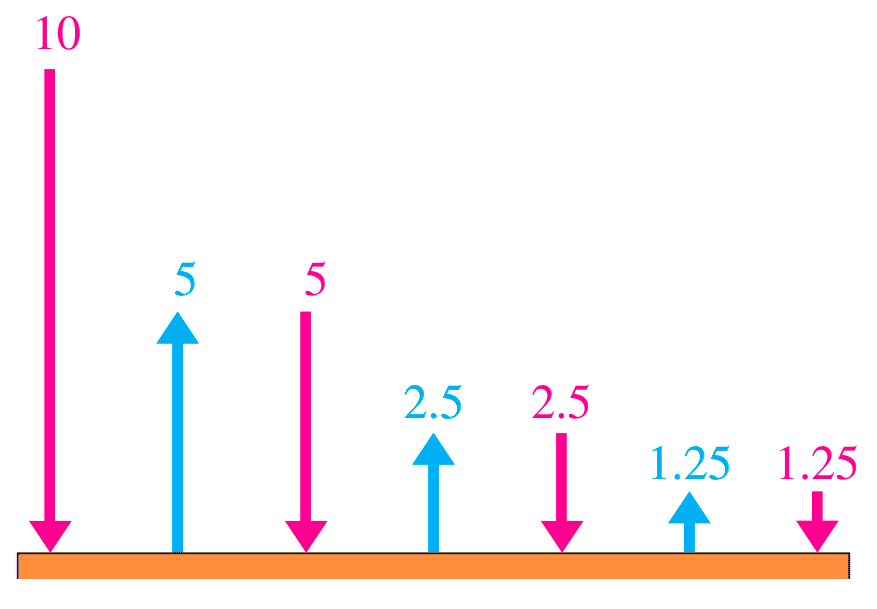
Consideramos el recorrido completo: primero la pelota cae 10 m, luego rebota hacia arriba una altura de 10 ⋅ 1/2 = 5 m y vuelve a caer esos mismos 5 m; en el siguiente rebote sube 5 ⋅ 1/2 = 2,5 m y cae 2,5 m, y así sucesivamente. Las distancias de caída y subida forman una progresión geométrica infinita.

La caída inicial es a₁ = 10 m. Después de eso, cada par de subida y caída tiene una distancia total igual al doble de la altura de rebote. Las alturas de rebote sucesivas son: 5, 2,5, 1,25,..., que constituyen una progresión geométrica con primer término 5 y razón r = 1/2. La suma de todas las distancias recorridas después de la primera caída es la suma infinita de los términos de esta última progresión multiplicada por 2 (porque cada rebote incluye subida y caída), más la caída inicial.

Calculamos primero la suma infinita de las alturas de rebote:

\(S_{\infty}=\dfrac{5}{1-\dfrac{1}{2}}=\dfrac{5}{\dfrac{1}{2}}=10\)

Esto significa que la suma de todas las alturas de rebote es 10 m. Como cada rebote implica subir y bajar, la distancia total correspondiente a rebotes es 2 ⋅ 10 = 20 m. Agregamos la caída inicial de 10 m:

\(\text{Distancia total}=10+20=30 \text{ metros}\)

Por lo tanto, la pelota recorre un total de 30 metros antes de detenerse.

Ejercicio 14

Una bomba de vacío saca la mitad del aire de un recipiente en cada carrera del pistón. Después de 10 carreras del pistón, ¿qué porcentaje de la cantidad original de aire continúa en el recipiente?

Solución

Si en cada carrera se extrae la mitad del aire presente, entonces queda la otra mitad. Es decir, después de cada carrera la cantidad de aire se multiplica por 1/2. Partiendo de una cantidad original que podemos considerar como el 100% (o 1 en términos de fracción), después de n carreras la fracción de aire que queda es \(\left(\dfrac{1}{2}\right)^n.\)

Para n = 10:

\(\text{Fracción restante}=\left(\dfrac{1}{2}\right)^{10}=\dfrac{1}{1024}\)

Convertimos a porcentaje multiplicando por 100:

\(\text{Porcentaje}=\dfrac{1}{1024}\cdot 100≈0,09765625%\)

Redondeando a dos decimales, el porcentaje de aire original que permanece es aproximadamente 0,10%.

Bibliografía

• Baldor, A. (1980). Álgebra. Codice.
• Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.