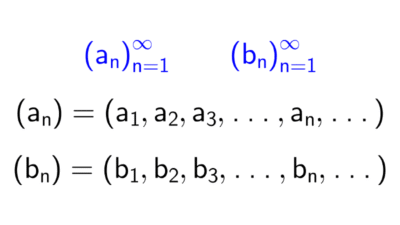
Ejercicios resueltos de sucesiones numéricas
A continuación veremos una serie de problemas resueltos sobre sucesiones infinitas de números reales: cálculo de términos, fórmula general, análisis de convergencia, monotonía, recursividad y problemas de la vida cotidiana, entre otros temas.
Índice
Conceptos básicos
Los siguientes artículos contienen teoría básica de las sucesiones junto con ejemplos explicativos.
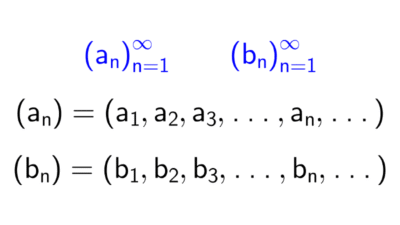
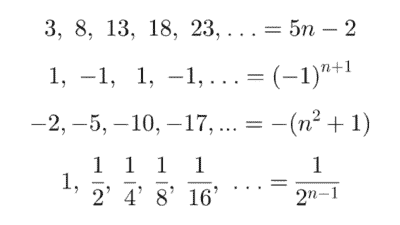
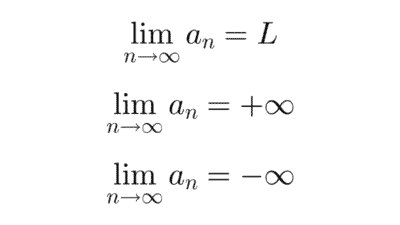

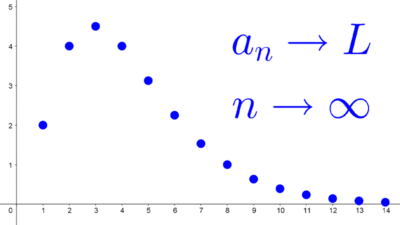
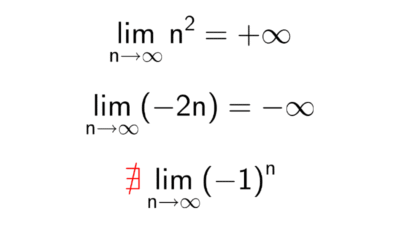
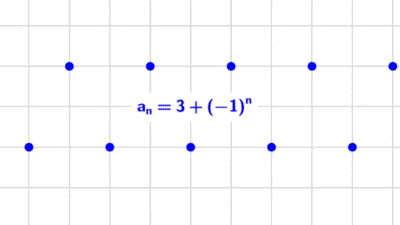
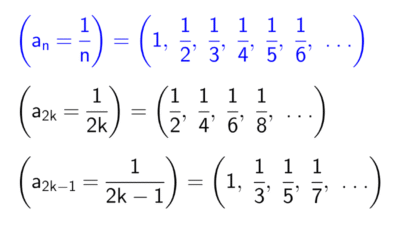
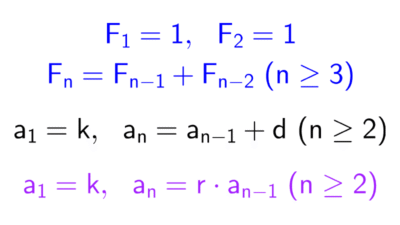
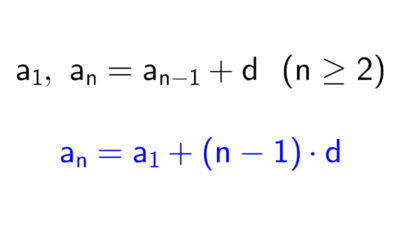
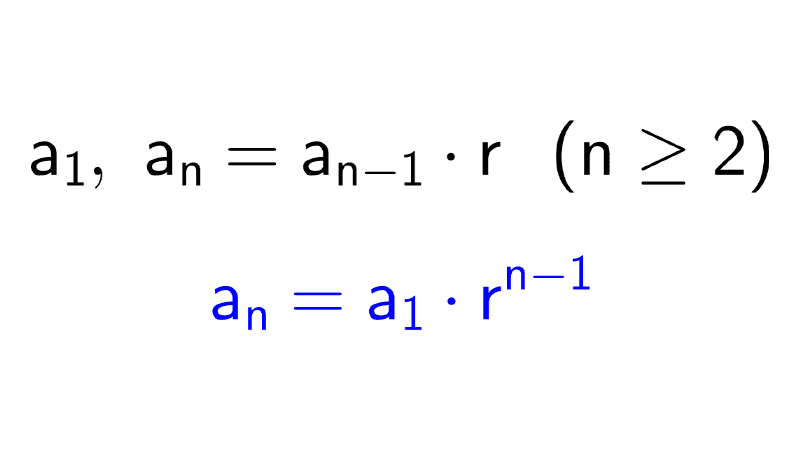
Calcular términos de sucesiones
Los siguientes ejercicios consisten en encontrar los primeros términos de una sucesión numérica.
Ejercicio 1
Escribir los primeros cinco términos de cada sucesión dado su término general.
- \(a_n=2n+5\)
- \(a_n=5+(-1)^n\)
- \(a_n=3^n\)
- \(a_n=\dfrac{(-1)^n}{n}\)
- \(a_n=\dfrac{2n}{n+3}\)
- \(a_n=\left(\dfrac{-1}{4}\right)^n\)
- \(a_n=\sin\dfrac{n\pi}{2}\)
- \(a_n=\dfrac{(-1)^{n(n+1)/2}}{n^2}\)
- \(a_n=5-\dfrac{1}{n}+\dfrac{1}{n^2}\)
- \(a_n=\dfrac{3^n}{n!}\)
Solución 1
La sucesión tiene término general \(a_n=2n+5.\) Este nos indica una regla simple: para cada posición \(n,\) multiplicamos por 2 y luego sumamos 5.
Para obtener los primeros cinco términos debemos sustituir \(n\) por los valores 1, 2, 3, 4 y 5.
Así, para \(n=1\) tenemos
\(a_1=2\cdot 1+5=2+5=7\)
Para \(n=2:\)
\(a_2=2\cdot 2+5=4+5=9\)
Luego, seguimos con los demás valores:
\(a_3=2\cdot 3+5=6+5=11\)
\(a_4=2\cdot 4+5=8+5=13\)
\(a_5=2\cdot 5+5=10+5=15\)
Por lo tanto, los primeros cinco términos de la sucesión son 7, 9, 11, 13, 15. Observamos que se trata de una progresión aritmética con diferencia 2, pues cada término se obtiene sumando dos al anterior.
Solución 2
Para obtener los primeros cinco términos de la sucesión \(a_n=5+(-1)^n\) sustituimos \(n\) por \(1, 2, 3, 4, 5.\) Cuando \(n\) es impar, \((-1)^n=-1;\) cuando es par, \((-1)^n=1.\) Así, calculamos:
\(a_1=5+(-1)^1=5-1=4\)
\(a_2=5+(-1)^2=5+1=6\)
\(a_3=5+(-1)^3=5-1=4\)
\(a_4=5+(-1)^4=5+1=6\)
\(a_5=5+(-1)^5=5-1=4\)
Por tanto, los cinco primeros términos son 4, 6, 4, 6, 4. Observamos que la sucesión oscila entre 4 y 6 según la paridad de \(n.\)
Solución 3
La sucesión \(a_n=3^n\) crece rápidamente. Hallamos los primeros términos reemplazando \(n\) por 1, 2, 3, 4, 5:
\(a_1=3^1=3\)
\(a_2=3^2=9\)
\(a_3=3^3=27\)
\(a_4=3^4=81\)
\(a_5=3^5=243\)
Así, los términos son 3, 9, 27, 81, 243, formando una progresión geométrica de razón 3, ya que cada término se obtiene multiplicando por 3 el anterior.
Solución 4
Para \(a_n=\dfrac{(-1)^n}{n},\) determinamos los valores para \(n=1,2,3,4,5:\)
\(a_1=\dfrac{(-1)^1}{1}=-1\)
\(a_2=\dfrac{(-1)^2}{2}=\dfrac{1}{2}\)
\(a_3=\dfrac{(-1)^3}{3}=-\dfrac{1}{3}\)
\(a_4=\dfrac{(-1)^4}{4}=\dfrac{1}{4}\)
\(a_5=\dfrac{(-1)^5}{5}=-\dfrac{1}{5}\)
Los primeros cinco términos son \(-1,\) \(\dfrac{1}{2},\) \(-\dfrac{1}{3},\) \(\dfrac{1}{4},\) \(-\dfrac{1}{5}.\) La sucesión alterna signos y sus valores absolutos decrecen.
Solución 5
En \(a_n=\dfrac{2n}{n+3}\) sustituimos \(n=1,2,3,4,5\) y simplificamos:
\(a_1=\dfrac{2\cdot 1}{1+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(a_2=\dfrac{4}{2+3}=\dfrac{4}{5}\)
\(a_3=\dfrac{6}{3+3}=\dfrac{6}{6}=1\)
\(a_4=\dfrac{8}{4+3}=\dfrac{8}{7}\)
\(a_5=\dfrac{10}{5+3}=\dfrac{10}{8}=\dfrac{5}{4}\)
Obtenemos \(\dfrac{1}{2},\) \(\dfrac{4}{5},\) \(1,\) \(\dfrac{8}{7},\) \(\dfrac{5}{4}.\)
Solución 6
Para \(a_n=\left(-\dfrac{1}{4}\right)^n\) calculamos las potencias sucesivas. Observamos que el signo alterna según \(n\) par o impar:
\(a_1=\left(-\dfrac{1}{4}\right)^1=-\dfrac{1}{4}\)
\(a_2=\left(-\dfrac{1}{4}\right)^2=\dfrac{1}{16}\)
\(a_3=\left(-\dfrac{1}{4}\right)^3=-\dfrac{1}{64}\)
\(a_4=\left(-\dfrac{1}{4}\right)^4=\dfrac{1}{256}\)
\(a_5=\left(-\dfrac{1}{4}\right)^5=-\dfrac{1}{1024}\)
Así, los términos son \(-\dfrac{1}{4},\) \(\dfrac{1}{16},\) \(-\dfrac{1}{64},\) \(\dfrac{1}{256},\) \(-\dfrac{1}{1024},\) una sucesión geométrica de razón \(-\dfrac{1}{4}.\)
Solución 7
Hallamos \(a_n=\sin\dfrac{n\pi}{2}\) para \(n=1,2,3,4,5.\) Recordamos los valores del seno en los ángulos \(\dfrac{\pi}{2},\) \(\pi,\) \(\dfrac{3\pi}{2},\) \(2\pi,\) \(\dfrac{5\pi}{2}:\)
\(a_1=\sin\dfrac{\pi}{2}=1\)
\(a_2=\sin\pi=0\)
\(a_3=\sin\dfrac{3\pi}{2}=-1\)
\(a_4=\sin 2\pi=0\)
\(a_5=\sin\dfrac{5\pi}{2}=\sin\left(2\pi+\dfrac{\pi}{2}\right)=\sin\dfrac{\pi}{2}=1\)
Por tanto, los primeros términos son 1, 0, -1, 0, 1.
Solución 8
Para \(a_n=\dfrac{(-1)^{n(n+1)/2}}{n^2}\) primero evaluamos el exponente del \(-1\) para cada \(n:\)
\(n=1:\) \(\dfrac{1\cdot 2}{2}=1,\) \((-1)^1=-1,\) \(a_1=\dfrac{-1}{1^2}=-1\)
\(n=2:\) \(\dfrac{2\cdot 3}{2}=3,\) \((-1)^3=-1,\) \(a_2=\dfrac{-1}{4}=-\dfrac{1}{4}\)
\(n=3:\) \(\dfrac{3\cdot 4}{2}=6,\) \((-1)^6=1,\) \(a_3=\dfrac{1}{9}\)
\(n=4:\) \(\dfrac{4\cdot 5}{2}=10,\) \((-1)^{10}=1,\) \(a_4=\dfrac{1}{16}\)
\(n=5:\) \(\dfrac{5\cdot 6}{2}=15,\) \((-1)^{15}=-1,\) \(a_5=\dfrac{-1}{25}=-\dfrac{1}{25}\)
Los primeros cinco términos son \(-1,\) \(-\dfrac{1}{4},\) \(\dfrac{1}{9},\) \(\dfrac{1}{16},\) \(-\dfrac{1}{25}.\)
Solución 9
En \(a_n=5-\dfrac{1}{n}+\dfrac{1}{n^2}\) reemplazamos \(n=1,2,3,4,5:\)
\(a_1=5-1+1=5\)
\(a_2=5-\dfrac{1}{2}+\dfrac{1}{4}=5-\dfrac{2}{4}+\dfrac{1}{4}=5-\dfrac{1}{4}=\dfrac{20}{4}-\dfrac{1}{4}=\dfrac{19}{4}\)
\(a_3=5-\dfrac{1}{3}+\dfrac{1}{9}=5-\dfrac{3}{9}+\dfrac{1}{9}=5-\dfrac{2}{9}=\dfrac{45}{9}-\dfrac{2}{9}=\dfrac{43}{9}\)
\(a_4=5-\dfrac{1}{4}+\dfrac{1}{16}=5-\dfrac{4}{16}+\dfrac{1}{16}=5-\dfrac{3}{16}=\dfrac{80}{16}-\dfrac{3}{16}=\dfrac{77}{16}\)
\(a_5=5-\dfrac{1}{5}+\dfrac{1}{25}=5-\dfrac{5}{25}+\dfrac{1}{25}=5-\dfrac{4}{25}=\dfrac{125}{25}-\dfrac{4}{25}=\dfrac{121}{25}\)
Obtenemos \(5,\) \(\dfrac{19}{4},\) \(\dfrac{43}{9},\) \(\dfrac{77}{16},\) \(\dfrac{121}{25}.\)
Solución 10
Para \(a_n=\dfrac{3^n}{n!}\) necesitamos los factoriales de 1 a 5: \(1!=1,\) \(2!=2,\) \(3!=6,\) \(4!=24,\) \(5!=120.\) Calculamos:
\(a_1=\dfrac{3^1}{1!}=\dfrac{3}{1}=3\)
\(a_2=\dfrac{3^2}{2!}=\dfrac{9}{2}\)
\(a_3=\dfrac{3^3}{3!}=\dfrac{27}{6}=\dfrac{9}{2}\)
\(a_4=\dfrac{3^4}{4!}=\dfrac{81}{24}=\dfrac{27}{8}\)
\(a_5=\dfrac{3^5}{5!}=\dfrac{243}{120}=\dfrac{81}{40}\)
Los primeros términos son \(3,\) \(\dfrac{9}{2},\) \(\dfrac{9}{2},\) \(\dfrac{27}{8},\) \(\dfrac{81}{40},\) alcanzando un máximo en \(n=2\) y \(n=3\) y luego decreciendo.
Ejercicio 2
En las siguientes sucesiones recurrentes, calcular los cinco términos que siguen a los términos iniciales dados.
- \(a_1=3, a_n=2(a_{n-1}-1)\)
- \(a_1=4, a_n=\dfrac{n+1}{2}a_{n-1}\)
- \(a_1=1, a_n=\dfrac{1}{1+a_{n-1}}\)
- \(a_1=6, a_n=\dfrac{a_{n-1}^2}{3}\)
- \(a_1=1, a_2=2, a_n=a_{n-1}+2a_{n-2}\)
Solución 1
Partimos de \(a_1=3\) y aplicamos la regla \(a_n=2(a_{n-1}-1)\) para \(n=2,3,4,5,6:\)
\(a_2=2(3-1)=2\cdot 2=4\)
\(a_3=2(4-1)=2\cdot 3=6\)
\(a_4=2(6-1)=2\cdot 5=10\)
\(a_5=2(10-1)=2\cdot 9=18\)
\(a_6=2(18-1)=2\cdot 17=34\)
Los términos que siguen al primero son 4, 6, 10, 18, 34.
Solución 2
Con \(a_1=4\) y \(a_n=\dfrac{n+1}{2}\,a_{n-1}\) obtenemos:
\(a_2=\dfrac{2+1}{2}\cdot 4=\dfrac{3}{2}\cdot 4=6\)
\(a_3=\dfrac{3+1}{2}\cdot 6=\dfrac{4}{2}\cdot 6=2\cdot 6=12\)
\(a_4=\dfrac{4+1}{2}\cdot 12=\dfrac{5}{2}\cdot 12=30\)
\(a_5=\dfrac{5+1}{2}\cdot 30=\dfrac{6}{2}\cdot 30=3\cdot 30=90\)
\(a_6=\dfrac{6+1}{2}\cdot 90=\dfrac{7}{2}\cdot 90=315\)
Los cinco términos siguientes a \(a_1\) son 6, 12, 30, 90, 315.
Solución 3
Dado \(a_1=1\) y \(a_n=\dfrac{1}{1+a_{n-1}}:\)
\(a_2=\dfrac{1}{1+1}=\dfrac{1}{2}\)
\(a_3=\dfrac{1}{1+\dfrac{1}{2}}=\dfrac{1}{\dfrac{3}{2}}=\dfrac{2}{3}\)
\(a_4=\dfrac{1}{1+\dfrac{2}{3}}=\dfrac{1}{\dfrac{5}{3}}=\dfrac{3}{5}\)
\(a_5=\dfrac{1}{1+\dfrac{3}{5}}=\dfrac{1}{\dfrac{8}{5}}=\dfrac{5}{8}\)
\(a_6=\dfrac{1}{1+\dfrac{5}{8}}=\dfrac{1}{\dfrac{13}{8}}=\dfrac{8}{13}\)
Así, los cinco términos posteriores al primero son \(\dfrac{1}{2},\) \(\dfrac{2}{3},\) \(\dfrac{3}{5},\) \(\dfrac{5}{8},\) \(\dfrac{8}{13}.\)
Solución 4
Con \(a_1=6\) y \(a_n=\dfrac{a_{n-1}^2}{3}:\)
\(a_2=\dfrac{6^2}{3}=\dfrac{36}{3}=12\)
\(a_3=\dfrac{12^2}{3}=\dfrac{144}{3}=48\)
\(a_4=\dfrac{48^2}{3}=\dfrac{2304}{3}=768\)
\(a_5=\dfrac{768^2}{3}=\dfrac{589824}{3}=196608\)
\(a_6=\dfrac{196608^2}{3}=\dfrac{38654705664}{3}=12884901888\)
Los términos que siguen al inicial son 12, 48, 768, 196608, 12884901888.
Solución 5
Partimos de \(a_1=1\) y \(a_2=2\) y usamos \(a_n=a_{n-1}+2a_{n-2}:\)
\(a_3=a_2+2a_1=2+2\cdot 1=2+2=4\)
\(a_4=a_3+2a_2=4+2\cdot 2=4+4=8\)
\(a_5=a_4+2a_3=8+2\cdot 4=8+8=16\)
\(a_6=a_5+2a_4=16+2\cdot 8=16+16=32\)
\(a_7=a_6+2a_5=32+2\cdot 16=32+32=64\)
Los cinco términos que siguen a los dos iniciales son 4, 8, 16, 32, 64. Observamos que, a partir del tercero, cada término duplica al anterior.
Determinar el término general
El término general de una sucesión permite obtener cualquier término conociendo solo su posición en la secuencia.
Ejercicio
Hallar el término general de las siguiente sucesiones dados sus primeros términos.
- \(2, 4, 8, 16, …\)
- \(1, 4, 7, 10, …\)
- \(1, \dfrac{3}{4}, \dfrac{5}{9}, \dfrac{7}{16}, \dfrac{9}{25}, …\)
- \(0, 2, 0, 2, 0, 2, 0, …\)
- \(-\dfrac{1}{3}, \dfrac{1}{9}, -\dfrac{1}{27}, \dfrac{1}{81},...\)
- \(5, -25, 125, -625, …\)
- \(\dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \dfrac{6}{7}, …\)
- \(\dfrac{7}{2}, 4, \dfrac{9}{2}, 5, …\)
Solución 1
Observamos la sucesión 2, 4, 8, 16, … Cada término se obtiene multiplicando el anterior por 2, lo que indica una progresión geométrica con razón \(r=2.\) El primer término es \(a_1=2.\)
Para una progresión geométrica, el término general es \(a_n=a_1\cdot r^{\,n-1}.\) Sustituyendo obtenemos:
\(a_n=2\cdot 2^{n-1}=2^n\)
Verificamos la fórmula con los primeros términos:
Para \(n=1:\) \(2^1=2\)
Para \(n=2:\) \(2^2=4\)
Para \(n=3:\) \(2^3=8\)
La expresión \(a_n=2^n\) reproduce correctamente la sucesión.
Solución 2
La sucesión 1, 4, 7, 10,… presenta una diferencia constante entre términos consecutivos:
\(4-1=3,\quad 7-4=3,\quad 10-7=3\)
Por tanto, es una progresión aritmética con primer término \(a_1=1\) y diferencia \(d=3.\)
El término general de una progresión aritmética es \(a_n=a_1+(n-1)d.\) Sustituyendo:
\(a_n=1+(n-1)\cdot 3=1+3n-3=3n-2\)
Comprobamos:
Para \(n=1:\) \(3\cdot 1-2=1\)
Para \(n=2:\) \(3\cdot 2-2=4\)
Para \(n=3:\) \(3\cdot 3-2=7\)
La fórmula \(a_n=3n-2\) es válida.
Solución 3
Analizamos la sucesión \(1,\ \dfrac{3}{4},\ \dfrac{5}{9},\ \dfrac{7}{16},\ \dfrac{9}{25},\ldots\)
Los numeradores son 1, 3, 5, 7, 9,… que corresponden a los números impares. Podemos expresar un número impar cualquiera como \(2n-1.\)
Los denominadores son 1, 4, 9, 16, 25,… que son los cuadrados perfectos, es decir, \(n^2.\)
Así, el término general resulta:
\(a_n=\dfrac{2n-1}{n^2}\)
Verificamos:
Para \(n=1:\) \(\dfrac{2\cdot 1-1}{1^2}=\dfrac{1}{1}=1\)
Para \(n=2:\) \(\dfrac{3}{4}\)
Para \(n=3:\) \(\dfrac{5}{9}\)
La expresión genera correctamente la sucesión.
Solución 4
La sucesión 0, 2, 0, 2, 0, 2,… alterna entre 0 para las posiciones impares y 2 para las pares.
Buscamos una expresión que tome el valor 2 cuando \(n\) es par y 0 cuando \(n\) es impar. Observamos que \(1+(-1)^n\) cumple esa condición:
Si \(n\) es par, \((-1)^n=1\) y \(1+1=2.\)
Si \(n\) es impar, \((-1)^n=-1\) y \(1-1=0.\)
Por tanto:
\(a_n=1+(-1)^n\)
Comprobamos:
Para \(n=1:\) \(1+(-1)^1=0\)
Para \(n=2:\) \(1+1=2\)
Para \(n=3:\) \(1+(-1)=0\)
La fórmula reproduce el patrón.
Solución 5
La sucesión de fracciones \(-\dfrac{1}{3}, \dfrac{1}{9},-\dfrac{1}{27}, \dfrac{1}{81},\ldots\) tiene términos que alternan signo y cuyos valores absolutos son potencias de \(\dfrac{1}{3}.\)
Observamos:
El primer término es \(-\dfrac{1}{3}=\left(-\dfrac{1}{3}\right)^1\)
El segundo es \(\dfrac{1}{9}=\left(-\dfrac{1}{3}\right)^2\)
El tercero es \(-\dfrac{1}{27}=\left(-\dfrac{1}{3}\right)^3\)
Se trata de una progresión geométrica con primer término \(a_1=-\dfrac{1}{3}\) y razón \(r=-\dfrac{1}{3}.\) El término general es:
\(a_n=a_1\cdot r^{\,n-1}=\left(-\dfrac{1}{3}\right)\cdot \left(-\dfrac{1}{3}\right)^{n-1}=\left(-\dfrac{1}{3}\right)^n\)
Verificamos:
Para \(n=1:\) \(\left(-\dfrac{1}{3}\right)^1=-\dfrac{1}{3}\)
Para \(n=2:\) \(\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
Para \(n=3:\) \(\left(-\dfrac{1}{3}\right)^3=-\dfrac{1}{27}\)
La fórmula es correcta.
Solución 6
La sucesión 5, –25, 125, –625,… alterna signo y los valores absolutos son potencias de 5: \(5^1, 5^2, 5^3, 5^4,\ldots\) El signo es positivo para las posiciones impares y negativo para las pares.
Podemos conseguir la alternancia de signo mediante \((-1)^{n-1},\) que vale 1 para \(n\) impar y –1 para \(n\) par. Multiplicando por \(5^n\) obtenemos:
\(a_n=(-1)^{n-1}\cdot 5^n\)
Comprobamos:
Para \(n=1:\) \((-1)^0\cdot 5^1=5\)
Para \(n=2:\) \((-1)^1\cdot 5^2=-25\)
Para \(n=3:\) \((-1)^2\cdot 5^3=125\)
La expresión genera la sucesión deseada.
Solución 7
En la sucesión \(\dfrac{3}{4},\ \dfrac{4}{5},\ \dfrac{5}{6},\ \dfrac{6}{7},\ldots\) observamos que tanto el numerador como el denominador aumentan en una unidad respecto al término anterior.
Para el término \(n\) -ésimo, el numerador es \(n+2\) y el denominador es \(n+3.\) Así:
\(a_n=\dfrac{n+2}{n+3}\)
Verificamos:
Para \(n=1:\) \(\dfrac{1+2}{1+3}=\dfrac{3}{4}\)
Para \(n=2:\) \(\dfrac{4}{5}\)
Para \(n=3:\) \(\dfrac{5}{6}\)
La expresión es correcta.
Solución 8
Analizamos la sucesión \(\dfrac{7}{2},\ 4,\ \dfrac{9}{2},\ 5,\ldots\) Escribimos todos los términos con denominador 2 para identificar el patrón:
\(\dfrac{7}{2},\ \dfrac{8}{2},\ \dfrac{9}{2},\ \dfrac{10}{2},\ldots\)
Los numeradores forman la sucesión 7, 8, 9, 10,… que corresponde a \(n+6\) (pues para \(n=1\) obtenemos 7, para \(n=2\) obtenemos 8, etcétera). Por tanto:
\(a_n=\dfrac{n+6}{2}\)
Comprobamos:
Para \(n=1:\) \(\dfrac{7}{2}\)
Para \(n=2:\) \(\dfrac{8}{2}=4\)
Para \(n=3:\) \(\dfrac{9}{2}=4,5\)
Para \(n=4:\) \(\dfrac{10}{2}=5\)
La fórmula genera correctamente la sucesión.
Análisis de sucesiones
Los siguientes problemas consisten en analizar el comportamiento de una sucesión, es decir, su convergencia o divergencia, límite, monotonía y acotación.
Crecimiento, decrecimiento y cotas
Una sucesión es creciente cuando cada término es mayor o igual al anterior, es decreciente si cada término es menor o igual al anterior, y es constante si todos los términos son iguales. Una sucesión que es siempre creciente o siempre decreciente se llama monótona.
La sucesión está acotada superiormente si existe un número real (cota superior) que ningún término puede superar, y acotada inferiormente si hay un número real (cota inferior) tal que ningún término es menor que él. La sucesión se dice que está acotada si lo está superior e inferiormente.
Ejercicio
Determinar si la sucesión dada es creciente, decreciente o es no monótona. ¿Está acotada la sucesión?
- \(a_n=(-2)^{n+1}\)
- \(a_n=\dfrac{n}{n^2+1}\)
- \(a_n=n(-1)^n\)
- \(a_n=\dfrac{2n-3}{3n+4}\)
- \(a_n=ne^{-n}\)
- \(a_n=\dfrac{2^n}{n!}\)
- \(a_n=n+\dfrac{1}{n}\)
- \(a_n=\dfrac{n}{2^{n+2}}\)
- \(a_n=\left(-\dfrac{2}{3}\right)^n\)
- \(a_n=\dfrac{\sin\sqrt{n}}{n}\)
Solución 1
Analizamos la sucesión \(a_n=(-2)^{n+1}\) para determinar su monotonía y acotación.
Comenzamos escribiendo los primeros términos para tener una pista del comportamiento:
\(a_1=(-2)^{2}=4\)
\(a_2=(-2)^{3}=-8\)
\(a_3=(-2)^{4}=16\)
\(a_4=(-2)^{5}=-32\)
\(a_5=(-2)^{6}=64\)
Observamos que los términos alternan el signo: los de índice impar son positivos y los de índice par son negativos. Además, los valores absolutos crecen rápidamente: \(4, 8, 16, 32, 64,\ldots\) En valor absoluto, la sucesión es creciente, pero al alternar signo no podemos decir que la sucesión original sea creciente ni decreciente en sentido estricto. Por ejemplo, \(a_1=4\) es mayor que \(a_2=-8,\) pero \(a_2=-8\) es menor que \(a_3=16.\) La sucesión no cumple \(a_n ≤ a_{n+1}\) para todo \(n\) (creciente) ni \(a_n ≥ a_{n+1}\) para todo \(n\) (decreciente). Por tanto, es no monótona.
En cuanto a la acotación, los términos en valor absoluto toman valores cada vez más grandes: \(|a_n|=2^{n+1}.\) Esta expresión tiende a infinito cuando \(n\) crece. Por ello, la sucesión no está acotada superiormente ni inferiormente: para \(n\) impar grande, \(a_n\) es positivo y muy grande; para \(n\) par grande, \(a_n\) es negativo y muy grande en valor absoluto. Así, concluimos que la sucesión no está acotada.
Solución 2
Estudiamos la sucesión \(a_n=\dfrac{n}{n^2+1}.\)
Para determinar su monotonía, analizamos la diferencia entre términos consecutivos o el cociente, pero también podemos estudiar el comportamiento de la función asociada \(f(x)=\dfrac{x}{x^2+1}\) para \(x≥ 1.\)
Calculamos los primeros términos:
\(a_1=\dfrac{1}{1+1}=\dfrac{1}{2}=0,5\)
\(a_2=\dfrac{2}{4+1}=\dfrac{2}{5}=0,4\)
\(a_3=\dfrac{3}{9+1}=\dfrac{3}{10}=0,3\)
\(a_4=\dfrac{4}{16+1}=\dfrac{4}{17}≈0,2353\)
\(a_5=\dfrac{5}{25+1}=\dfrac{5}{26}≈0,1923\)
Parece que los términos decrecen. Para confirmarlo, podemos considerar la diferencia \(a_{n+1}-a_n\) y vemos su signo. Pero tenemos otra forma más sencilla: estudiamos la función \(f(x)=\dfrac{x}{x^2+1}.\)
Su derivada es
\(f'(x)=\dfrac{(x^2+1)-x\cdot 2x}{(x^2+1)^2}=\dfrac{1-x^2}{(x^2+1)^2}\)
Para \(x>1,\) \(f'(x)<0,\) lo que indica que la función es decreciente a partir de \(x=1.\) Como la sucesión son los valores de \(f\) en los enteros positivos, resulta que \(a_n\) es decreciente para \(n≥ 1.\) Comprobamos con \(a_1>a_2>a_3>\ldots\) Así, la sucesión es decreciente (estrictamente).
En cuanto a la acotación, al ser decreciente, el primer término es el mayor: \(a_1=\dfrac{1}{2}.\) Todos los términos son positivos, pues \(n>0\) y \(n^2+1>0.\) Además, tienden a 0 cuando \(n→\infty\) porque el denominador crece más rápido que el numerador. Por tanto, la sucesión está acotada inferiormente por 0 (sin alcanzarlo nunca) y superiormente por \(\dfrac{1}{2}.\) Concluimos que la sucesión está acotada, con \(0<a_n ≤ \dfrac{1}{2}.\)
Solución 3
Analizamos la sucesión \(a_n=n(-1)^n.\)
Escribimos los primeros términos:
\(a_1=1\cdot (-1)^1=-1\)
\(a_2=2\cdot (-1)^2=2\)
\(a_3=3\cdot (-1)^3=-3\)
\(a_4=4\cdot (-1)^4=4\)
\(a_5=5\cdot (-1)^5=-5\)
Observamos que los términos alternan el signo: los de índice impar son negativos y los de índice par son positivos. Además, los valores absolutos crecen linealmente: \(|a_n|=n.\) Al alternar signo, la sucesión no es creciente ni decreciente. Por tanto, la sucesión es no monótona.
Respecto a la acotación, los valores absolutos son \(|a_n|=n,\) que crecen sin límite cuando \(n\) aumenta. Así, la sucesión no está acotada superiormente (los términos pares se hacen arbitrariamente grandes) ni inferiormente (los términos impares se hacen arbitrariamente grandes en valor absoluto pero negativos). Concluimos que la sucesión no está acotada.
Solución 4
Consideramos \(a_n=\dfrac{2n-3}{3n+4}.\)
Para analizar la monotonía, podemos estudiar la diferencia \(a_{n+1}-a_n\) o el comportamiento asintótico. También podemos observar la función asociada \(f(x)=\dfrac{2x-3}{3x+4}\) para \(x≥ 1.\)
Calculamos algunos términos:
\(a_1=\dfrac{2-3}{3+4}=\dfrac{-1}{7}≈-0,1429\)
\(a_2=\dfrac{4-3}{6+4}=\dfrac{1}{10}=0,1\)
\(a_3=\dfrac{6-3}{9+4}=\dfrac{3}{13}≈0,2308\)
\(a_4=\dfrac{8-3}{12+4}=\dfrac{5}{16}=0,3125\)
\(a_5=\dfrac{10-3}{15+4}=\dfrac{7}{19}≈0,3684\)
Observamos que los términos aumentan: \(-0,1429<0,1<0,2308<0,3125<0,3684.\) Para confirmar, calculamos \(a_{n+1}-a_n:\)
\(a_{n+1}-a_n=\dfrac{2(n+1)-3}{3(n+1)+4}-\dfrac{2n-3}{3n+4}=\dfrac{2n-1}{3n+7}-\dfrac{2n-3}{3n+4}\)
Ponemos común denominador \((3n+7)(3n+4)\) y simplificamos el numerador:
\((2n-1)(3n+4)-(2n-3)(3n+7)=[6n^2+8n-3n-4]-[6n^2+14n-9n-21]=(6n^2+5n-4)-(6n^2+5n-21)=-4+21=17\)
Como \(17>0\) y el denominador \((3n+7)(3n+4)\) es positivo para \(n≥ 1,\) tenemos \(a_{n+1}-a_n>0.\) Así, la sucesión es creciente (estrictamente).
Para la acotación, observamos que cuando \(n\) crece, \(a_n\) se aproxima a \(\dfrac{2}{3}\) (cociente de los coeficientes directores). Siendo creciente, el primer término es el menor: \(a_1=-\dfrac{1}{7}.\) Todos los términos son menores que \(\dfrac{2}{3}\) y se acercan a este valor sin superarlo. Por tanto, la sucesión está acotada inferiormente por \(-\dfrac{1}{7}\) y superiormente por \(\dfrac{2}{3}\) (aunque no alcanza este último, es una cota). Concluimos que la sucesión está acotada, con \(-\dfrac{1}{7} ≤ a_n<\dfrac{2}{3}.\)
Solución 5
Estudiamos \(a_n=n e^{-n}=\dfrac{n}{e^n}.\) Para determinar la monotonía, analizamos la función asociada \(f(x)=x e^{-x}\) para \(x≥ 1.\) Calculamos su derivada:
\(f'(x)=e^{-x}+x(-e^{-x})=e^{-x}(1-x)\)
Para \(x>1,\) \(f'(x)<0,\) lo que indica que la función es decreciente a partir de \(x=1.\) Por tanto, la sucesión es decreciente para \(n≥ 1.\) Verificamos con los primeros términos:
\(a_1=1\cdot e^{-1}=\dfrac{1}{e}≈0,3679\)
\(a_2=2 e^{-2}=\dfrac{2}{e^2}≈0,2707\)
\(a_3=3 e^{-3}=\dfrac{3}{e^3}≈0,1494\)
\(a_4=4 e^{-4}≈0,0733\)
\(a_5=5 e^{-5}≈0,0337\)
Efectivamente, los términos decrecen: \(a_1>a_2>a_3>\ldots\) Así, la sucesión es decreciente (estrictamente).
En cuanto a la acotación, al ser decreciente, el primer término es el mayor: \(a_1=\dfrac{1}{e}.\) Todos los términos son positivos. Además, cuando \(n→\infty,\) \(a_n→0\) porque la exponencial crece más rápido que \(n.\) Por tanto, la sucesión está acotada inferiormente por 0 (sin alcanzarlo) y superiormente por \(\dfrac{1}{e}.\) Concluimos que la sucesión está acotada, con \(0<a_n ≤ \dfrac{1}{e}.\)
Solución 6
Analizamos la sucesión \(a_n=\dfrac{2^n}{n!}.\)
Para estudiar su monotonía, calculamos el cociente entre un término y el anterior, ya que al tratarse de factoriales y potencias esta expresión suele simplificarse bien.
\(\dfrac{a_{n+1}}{a_n}=\dfrac{2^{n+1}}{(n+1)!}\cdot \dfrac{n!}{2^n}=\dfrac{2}{n+1}\)
Observamos que este cociente es menor que 1 cuando \(n+1>2,\) es decir, cuando \(n>1,\) esto nos indica que la sucesión es decreciente, pues si \(\dfrac{a_{n+1}}{a_n}<1,\) entonces \(a_{n+1}<a_n\) cuando \(n>1.\)
Calculemos los primeros términos para confirmar:
\(a_1=\dfrac{2^1}{1!}=2\)
\(a_2=\dfrac{4}{2}=2\)
\(a_3=\dfrac{8}{6}=\dfrac{4}{3}≈1,333\)
\(a_4=\dfrac{16}{24}=\dfrac{2}{3}≈0,667\)
\(a_5=\dfrac{32}{120}=\dfrac{4}{15}≈0,267\)
Vemos que \(a_1=a_2\) y a partir de \(a_2\) los términos decrecen estrictamente: \(a_2>a_3>a_4>\ldots\) Por tanto, la sucesión es decreciente en sentido amplio.
Para la acotación, el valor más grande se alcanza en los dos primeros términos: \(a_1=a_2=2.\) Todos los términos son positivos y tienden a 0 cuando \(n\) crece, porque el factorial crece más rápido que la potencia. Así, la sucesión está acotada inferiormente por 0 (sin alcanzarlo) y superiormente por 2. Concluimos que la sucesión está acotada, con \(0<a_n ≤ 2.\)
Solución 7
Consideramos \(a_n=n+\dfrac{1}{n}.\) Para estudiar la monotonía, analizamos la diferencia entre términos consecutivos:
\(a_{n+1}-a_n=\left(n+1+\dfrac{1}{n+1}\right)-\left(n+\dfrac{1}{n}\right)=1+\dfrac{1}{n+1}-\dfrac{1}{n}\)
Simplificamos la parte fraccionaria: \(\dfrac{1}{n+1}-\dfrac{1}{n}=\dfrac{n-(n+1)}{n(n+1)}=-\dfrac{1}{n(n+1)}.\) Por tanto,
\(a_{n+1}-a_n=1-\dfrac{1}{n(n+1)}\)
Para \(n ≥ 1,\) \(n(n+1) ≥ 2,\) luego \(\dfrac{1}{n(n+1)} ≤ \dfrac{1}{2}<1.\) Así, la diferencia es positiva: \(a_{n+1}-a_n>0\) para todo \(n.\) Esto significa que la sucesión es creciente (estrictamente).
Verificamos con los primeros términos:
\(a_1=1+1=2\)
\(a_2=2+\dfrac{1}{2}=2,5\)
\(a_3=3+\dfrac{1}{3}≈3,333\)
\(a_4=4+\dfrac{1}{4}=4,25\)
\(a_5=5+\dfrac{1}{5}=5,2\)
Efectivamente, los términos aumentan.
En cuanto a la acotación, al ser creciente, el primer término es el menor: \(a_1=2.\) Cuando \(n\) crece, \(a_n\) se hace arbitrariamente grande porque el término \(n\) domina. Por tanto, no hay cota superior. La sucesión está acotada inferiormente por 2, pero no está acotada superiormente.
Solución 8
Estudiamos \(a_n=\dfrac{n}{2^{n+2}}.\) Podemos reescribirla como:
\(a_n=\dfrac{n}{4\cdot 2^n}=\dfrac{1}{4}\cdot \dfrac{n}{2^n}\)
Para analizar la monotonía, consideramos el cociente \(a_{n+1}/a_n:\)
\(\dfrac{a_{n+1}}{a_n}=\dfrac{n+1}{2^{(n+1)+2}}\cdot \dfrac{2^{n+2}}{n}=\dfrac{n+1}{n}\cdot \dfrac{2^{n+2}}{2^{n+3}}=\dfrac{n+1}{n}\cdot \dfrac{1}{2}=\dfrac{n+1}{2n}\)
Este cociente es menor que 1 cuando \(\dfrac{n+1}{2n}<1,\) es decir, \(n+1<2n,\) lo que equivale a \(1<n.\) Para \(n=1,\) el cociente vale \(\dfrac{2}{2}=1,\) luego \(a_2=a_1.\) Para \(n ≥ 2,\) el cociente es menor que 1, por lo que a partir de \(n=2\) los términos decrecen. Calculemos algunos valores:
\(a_1=\dfrac{1}{2^{3}}=\dfrac{1}{8}=0,125\)
\(a_2=\dfrac{2}{2^{4}}=\dfrac{2}{16}=0,125\)
\(a_3=\dfrac{3}{2^{5}}=\dfrac{3}{32}=0,09375\)
\(a_4=\dfrac{4}{2^{6}}=\dfrac{4}{64}=0,0625\)
\(a_5=\dfrac{5}{2^{7}}=\dfrac{5}{128}≈0,03906\)
Observamos que \(a_1=a_2\) y después decrece. Por tanto, la sucesión es decreciente en sentido amplio.
Para la acotación, el máximo valor se alcanza en los dos primeros términos: \(a_1=a_2=0,125.\) Todos los términos son positivos y tienden a 0 cuando \(n\) crece, pues el denominador exponencial crece más rápido que el numerador lineal. Así, la sucesión está acotada inferiormente por 0 y superiormente por 0,125. Concluimos que la sucesión está acotada, con \(0<a_n ≤ \dfrac{1}{8}.\)
Solución 9
Consideramos \(a_n=\left(-\dfrac{2}{3}\right)^n.\) Escribimos los primeros términos para observar el comportamiento:
\(a_1=-\dfrac{2}{3}≈-0,667\)
\(a_2=\dfrac{4}{9}≈0,444\)
\(a_3=-\dfrac{8}{27}≈-0,296\)
\(a_4=\dfrac{16}{81}≈0,198\)
\(a_5=-\dfrac{32}{243}≈-0,132\)
Los términos alternan el signo: negativos para \(n\) impar, positivos para \(n\) par. Además, los valores absolutos forman una progresión geométrica de razón \(\dfrac{2}{3}:\) \(|a_n|=\left(\dfrac{2}{3}\right)^n,\) que es decreciente. Al alternar signo, la sucesión no es creciente ni decreciente, pues por ejemplo \(a_1=-0,667<a_2=0,444,\) pero \(a_2=0,444>a_3=-0,296.\) No se cumple \(a_n ≤ a_{n+1}\) para todo \(n\) ni \(a_n ≥ a_{n+1}\) para todo \(n.\) Por tanto, es no monótona.
En cuanto a la acotación, los valores absolutos están acotados por \(\left(\dfrac{2}{3}\right)^1=\dfrac{2}{3},\) y además tienden a 0 cuando \(n\) crece. Por tanto, todos los términos cumplen \(|a_n| ≤ \dfrac{2}{3}.\) Así, la sucesión está acotada inferiormente por \(-\dfrac{2}{3}\) y superiormente por \(\dfrac{2}{3}.\) Concluimos que la sucesión está acotada.
Solución 10
Analizamos \(a_n=\dfrac{\sin\sqrt{n}}{n}.\)
Para estudiar la monotonía, observamos que el numerador \(\sin\sqrt{n}\) oscila entre -1 y 1, tomando valores positivos y negativos de forma irregular, pues \(\sqrt{n}\) no es un múltiplo entero de \(\pi.\) Esto hace que la sucesión no sea monótona: no podemos asegurar que los términos crezcan o decrezcan sistemáticamente, ya que el signo y la magnitud del seno varían.
Para la acotación, usamos que \(|\sin\sqrt{n}| ≤ 1.\) Entonces:
\(|a_n|=\dfrac{|\sin\sqrt{n}|}{n} ≤ \dfrac{1}{n}\)
Como \(\dfrac{1}{n}\) tiende a 0 y está acotado por 1, tenemos que \(|a_n| ≤ 1\) para todo \(n,\) es decir, \(-1 ≤ a_n ≤ 1.\) La sucesión está acotada inferiormente por -1 y superiormente por 1. Concluimos que la sucesión está acotada.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Convergencia y divergencia
Una sucesión convergente es aquella cuyos términos se acercan a un valor fijo a medida que se avanza en la sucesión. Una sucesión divergente es aquella en la que no ocurre eso, es decir, sus términos crecen o decrecen sin límite u oscilan.
Ejercicio
Determinar la convergencia o divergencia de cada sucesión dado su término enésimo. Si la sucesión converge, encontrar su límite.
- \(a_n=(1/3)^n -1\)
- \(a_n=\dfrac{5}{n+2}\)
- \(a_n=4-\dfrac{3}{n}\)
- \(a_n=\dfrac{2}{n!}\)
- \(a_n=(-1)^n \dfrac{n}{n+1}\)
- \(a_n=1+(-1)^n\)
- \(a_n=\dfrac{3^n}{4^n}\)
- \(a_n=\left(1+\dfrac{1}{n}\right)^n\)
- \(a_n=\dfrac{\sin n}{n}\)
- \(a_n=\sqrt{n+1}-\sqrt{n}\)
Solución 1
Estudiamos la convergencia de la sucesión \(a_n=\left(\dfrac{1}{3}\right)^n-1.\)
Observamos que \(\left(\dfrac{1}{3}\right)^n\) es una potencia con base menor que 1 y positiva. Cuando \(n\) crece indefinidamente, esta potencia tiende a 0:
\(\lim_{n→\infty} \left(\dfrac{1}{3}\right)^n=0\)
Por tanto, el límite de \(a_n\) es:
\(\lim_{n→\infty} a_n=\lim_{n→\infty} \left[\left(\dfrac{1}{3}\right)^n-1\right]=0-1=-1\)
Como el límite existe y es un número finito, la sucesión converge y su límite es \(-1.\)
Podemos verificar con algunos términos:
\(a_1=\dfrac{1}{3}-1=-\dfrac{2}{3}≈-0,667\)
\(a_2=\dfrac{1}{9}-1=-\dfrac{8}{9}≈-0,889\)
\(a_3=\dfrac{1}{27}-1=-\dfrac{26}{27}≈-0,963\)
\(a_4=\dfrac{1}{81}-1=-\dfrac{80}{81}≈-0,988\)
Los términos se acercan cada vez más a \(-1.\)
Solución 2
Consideramos \(a_n=\dfrac{5}{n+2}.\)
Cuando \(n\) tiende a infinito, el denominador \(n+2\) crece sin límite, mientras que el numerador permanece constante. Por tanto, la fracción tiende a 0:
\(\lim_{n→\infty} \dfrac{5}{n+2}=0\)
El límite existe y es finito, así que la sucesión converge a \(0.\)
Solución 3
Estudiamos la convergencia de la sucesión \(a_n=4-\dfrac{3}{n}.\)
Cuando \(n\) crece indefinidamente, el término \(\dfrac{3}{n}\) se hace cada vez más pequeño, tendiendo a 0:
\(\lim_{n→\infty} \dfrac{3}{n}=0\)
Por tanto, el límite de \(a_n\) es:
\(\lim_{n→\infty} a_n=\lim_{n→\infty} \left(4-\dfrac{3}{n}\right)=4-0=4\)
El límite existe y es un número finito, así que la sucesión converge y su límite es \(4.\)
Podemos observar algunos términos para confirmar la tendencia:
\(a_1=4-3=1\)
\(a_2=4-\dfrac{3}{2}=4-1,5=2,5\)
\(a_3=4-1=3\)
\(a_4=4-\dfrac{3}{4}=4-0,75=3,25\)
\(a_5=4-\dfrac{3}{5}=4-0,6=3,4\)
Los términos aumentan acercándose a 4 desde abajo.
Solución 4
Consideramos \(a_n=\dfrac{2}{n!}.\)
El factorial \(n!\) crece muy rápidamente cuando \(n\) aumenta. Para \(n\) grande, \(n!\) se hace arbitrariamente grande, por lo que su inverso tiende a 0:
\(\lim_{n→\infty} \dfrac{2}{n!}=0\)
El límite existe y es finito, luego la sucesión converge a \(0.\)
Observamos los primeros términos:
\(a_1=\dfrac{2}{1!}=2\)
\(a_2=\dfrac{2}{2!}=\dfrac{2}{2}=1\)
\(a_3=\dfrac{2}{6}=\dfrac{1}{3}≈0,333\)
\(a_4=\dfrac{2}{24}=\dfrac{1}{12}≈0,0833\)
\(a_5=\dfrac{2}{120}=\dfrac{1}{60}≈0,0167\)
Efectivamente, los términos decrecen rápidamente hacia 0.
Solución 5
Analizamos la sucesión \(a_n=(-1)^n \dfrac{n}{n+1}.\)
El factor \((-1)^n\) hace que los términos alternen el signo: positivos para \(n\) par, negativos para \(n\) impar. Estudiamos por separado el comportamiento de la fracción \(\dfrac{n}{n+1}.\) Para determinar su límite cuando \(n\) tiende a infinito, dividimos numerador y denominador por \(n,\) que es la máxima potencia presente:
\(\dfrac{n}{n+1}=\dfrac{\dfrac{n}{n}}{\dfrac{n}{n}+\dfrac{1}{n}}=\dfrac{1}{1+\dfrac{1}{n}}\)
Cuando \(n→\infty,\) el término \(\dfrac{1}{n}\) tiende a 0, por lo que:
\(\lim_{n→\infty} \dfrac{n}{n+1}=\lim_{n→\infty} \dfrac{1}{1+\dfrac{1}{n}}=\dfrac{1}{1+0}=1\)
Por tanto, la fracción \(\dfrac{n}{n+1}\) converge a 1. Ahora, al multiplicarla por \((-1)^n,\) los términos para \(n\) par se aproximan a \(1,\) mientras que los términos para \(n\) impar se aproximan a \(-1.\) Al acercarse a dos valores distintos, la sucesión no tiene un límite único.
Podemos escribir algunos términos para visualizarlo:
\(a_1=(-1)^1\cdot \dfrac{1}{2}=-\dfrac{1}{2}=-0,5\)
\(a_2=(-1)^2\cdot \dfrac{2}{3}=\dfrac{2}{3}≈0,667\)
\(a_3=(-1)^3\cdot \dfrac{3}{4}=-\dfrac{3}{4}=-0,75\)
\(a_4=(-1)^4\cdot \dfrac{4}{5}=0,8\)
\(a_5=(-1)^5\cdot \dfrac{5}{6}≈-0,833\)
\(a_6=(-1)^6\cdot \dfrac{6}{7}≈0,857\)
Los términos pares se acercan a 1, los impares a \(-1.\) Como la sucesión oscila sin aproximarse a un único valor, concluimos que diverge (no tiene límite).
Solución 6
Estudiamos \(a_n=1+(-1)^n.\)
El término \((-1)^n\) vale 1 cuando \(n\) es par y \(-1\) cuando \(n\) es impar. Por tanto:
Si \(n\) es par: \(a_n=1+1=2.\)
Si \(n\) es impar: \(a_n=1-1=0.\)
La sucesión toma únicamente los valores 0 y 2, alternándolos:
\(a_1=0, a_2=2, a_3=0, a_4=2, a_5=0,\ldots\)
Al no acercarse a un único número (los términos oscilan constantemente entre 0 y 2), la sucesión no tiene límite. Por tanto, diverge.
Solución 7
Estudiamos la convergencia de la sucesión \(a_n=\dfrac{3^n}{4^n}.\)
Podemos reescribirla como una sola potencia:
\(a_n=\left(\dfrac{3}{4}\right)^n\)
Observamos que la base \(\dfrac{3}{4}\) es un número positivo menor que 1. Cuando \(n\) crece indefinidamente, una potencia con base en el intervalo \((0,1)\) tiende a 0:
\(\lim_{n→\infty} \left(\dfrac{3}{4}\right)^n=0\)
Por tanto, el límite de \(a_n\) es 0. El límite existe y es finito, así que la sucesión converge a \(0.\)
Podemos verificar con algunos términos:
\(a_1=\dfrac{3}{4}=0,75\)
\(a_2=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}=0,5625\)
\(a_3=\left(\dfrac{3}{4}\right)^3=\dfrac{27}{64}≈0,4219\)
\(a_4=\left(\dfrac{3}{4}\right)^4=\dfrac{81}{256}≈0,3164\)
\(a_5=\left(\dfrac{3}{4}\right)^5=\dfrac{243}{1024}≈0,2373\)
Los términos decrecen y se acercan a 0.
Solución 8
Consideramos la sucesión \(a_n=\left(1+\dfrac{1}{n}\right)^n.\)
Esta sucesión es muy conocida: cuando \(n\) tiende a infinito, sus términos se aproximan al número \(e,\) base de los logaritmos naturales. Podemos recordar que:
\(\lim_{n→\infty} \left(1+\dfrac{1}{n}\right)^n=e\)
El valor de \(e\) es aproximadamente \(2,71828\ldots\) Por tanto, la sucesión converge y su límite es \(e.\)
Observamos algunos términos para apreciar la tendencia:
\(a_1=(1+1)^1=2\)
\(a_2=\left(1+\dfrac{1}{2}\right)^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}=2,25\)
\(a_3=\left(1+\dfrac{1}{3}\right)^3=\left(\dfrac{4}{3}\right)^3=\dfrac{64}{27}≈2,370\)
\(a_4=\left(1+\dfrac{1}{4}\right)^4=\left(\dfrac{5}{4}\right)^4=\dfrac{625}{256}≈2,441\)
\(a_5=\left(1+\dfrac{1}{5}\right)^5=\left(\dfrac{6}{5}\right)^5=\dfrac{7776}{3125}≈2,488\)
Los valores aumentan y se acercan a \(e≈2,718.\)
Solución 9
Analizamos \(a_n=\dfrac{\sin n}{n}.\)
Para determinar su convergencia, utilizamos que la función seno está acotada: \(|\sin n| ≤ 1\) para todo \(n.\) Entonces:
\(|a_n|=\dfrac{|\sin n|}{n} ≤ \dfrac{1}{n}\)
Cuando \(n\) tiende a infinito, \(\dfrac{1}{n}\) tiende a 0. Por el teorema del sandwich (o decompresión), como \(0 ≤ |a_n| ≤ \dfrac{1}{n}\) y \(\dfrac{1}{n}→0,\) concluimos que \(|a_n|→0,\) y por tanto \(a_n→0.\)
El límite existe y es finito, así que la sucesión converge a \(0.\)
Observamos algunos términos para ver el comportamiento, aunque el seno introduce oscilaciones:
\(a_1=\sin 1≈0,8415\)
\(a_2=\dfrac{\sin 2}{2}≈\dfrac{0,9093}{2}=0,4547\)
\(a_3=\dfrac{\sin 3}{3}≈\dfrac{0,1411}{3}=0,0470\)
\(a_4=\dfrac{\sin 4}{4}≈\dfrac{-0,7568}{4}=-0,1892\)
\(a_5=\dfrac{\sin 5}{5}≈\dfrac{-0,9589}{5}=-0,1918\)
A pesar de las oscilaciones, los valores se van haciendo más pequeños en magnitud.
Solución 10
Estudiamos \(a_n=\sqrt{n+1}-\sqrt{n}.\)
Nos encontramos con una resta de dos términos que tienden a infinito, por lo que tenemos una indeterminación del tipo \(\infty-\infty.\) Para resolverla, multiplicamos y dividimos por el conjugado:
\(a_n=\left(\sqrt{n+1}-\sqrt{n}\right)\cdot \dfrac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}=\dfrac{(n+1)-n}{\sqrt{n+1}+\sqrt{n}}=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Ahora la expresión es más clara: cuando \(n\) crece, el denominador \(\sqrt{n+1}+\sqrt{n}\) tiende a infinito, por lo que la fracción tiende a 0:
\(\lim_{n→\infty} a_n=\lim_{n→\infty} \dfrac{1}{\sqrt{n+1}+\sqrt{n}}=0\)
El límite existe y es finito, así que la sucesión converge a \(0.\)
Observamos los primeros términos:
\(a_1=\sqrt{2}-1≈1,4142-1=0,4142\)
\(a_2=\sqrt{3}-\sqrt{2}≈1,7321-1,4142=0,3179\)
\(a_3=\sqrt{4}-\sqrt{3}=2-1,7321=0,2679\)
\(a_4=\sqrt{5}-\sqrt{4}≈2,2361-2=0,2361\)
\(a_5=\sqrt{6}-\sqrt{5}≈2,4495-2,2361=0,2134\)
Los términos positivos decrecen hacia 0.
Progresiones aritméticas y geométricas
Una progresión aritmética es aquella donde cada término, luego del primero, se obtiene sumando una constante fija (diferencia común) al término anterior. En una progresión geométrica, en cambio, cada término luego del primero se obtiene multiplicando el anterior por una constante fija distinta de cero, llamada razón común.
Sucesiones aritméticas
Ejercicio 1
Hallar el término general de una progresión aritmética cuya diferencia es 5 y el segundo término es 16.
Solución
En una progresión aritmética conocemos la diferencia \(d=5\) y el segundo término \(a_2=16.\) El término general de una progresión aritmética es \(a_n=a_1+(n-1)d.\) Primero debemos hallar el primer término \(a_1.\)
Sabemos que \(a_2=a_1+d.\) Sustituyendo los valores conocidos:
\(16=a_1+5→a_1=16-5=11\)
Ahora podemos escribir el término general:
\(a_n=11+(n-1)\cdot 5=11+5n-5=5n+6\)
Verificamos para \(n=2:\) \(a_2=5\cdot 2+6=10+6=16,\) que coincide con el dato. Por tanto, el término general es \(a_n=5n+6.\)
Ejercicio 2
Los lados de un cuadrilátero están en progresión aritmética de diferencia 6. Si el perímetro es de 100 cm, calcular las longitudes de sus lados.
Solución
Sea el cuadrilátero con lados en progresión aritmética de diferencia \(d=6.\) Llamamos \(a_1\) al lado menor, entonces los lados son \(a_1,\) \(a_1+6,\) \(a_1+12\) y \(a_1+18.\)
El perímetro es la suma de los cuatro lados:
\(a_1+(a_1+6)+(a_1+12)+(a_1+18)=4a_1+(6+12+18)=4a_1+36\)
Igualamos al perímetro dado, 100 cm:
\(4a_1+36=100→4a_1=64→a_1=16\)
Por tanto, las longitudes de los lados son:
\(16, 22, 28, 34 \text{ cm}\)
Ejercicio 3
Un deportista entrena tres semanas según el siguiente plan: el primer día corre 15 minutos e incrementa la duración de la carrera en 5 minutos cada día. ¿Cuánto tiempo corrió el último día?
Solución
El deportista corre durante 21 días (tres semanas). El primer día corre 15 minutos y cada día aumenta 5 minutos. Se trata de una progresión aritmética con primer término \(a_1=15\) y diferencia \(d=5.\)
El tiempo corrido el último día corresponde al término \(a_{21}.\) Usamos la fórmula del término general:
\(a_n=a_1+(n-1)d→a_{21}=15+(21-1)\cdot 5=15+20\cdot 5=15+100=115\)
Por tanto, el último día corrió 115 minutos, que equivalen a 1 hora y 55 minutos.
Ejercicio 4
Durante 15 días se observó el crecimiento del tallo de una semilla germinada. El primer día medía 10 mm y el último 80. ¿Cuánto creció diariamente si el tallo aumentó en una cantidad fija cada día?
Solución
Observamos el crecimiento del tallo durante 15 días. El primer día mide \(a_1=10\) mm y el último día (día 15) mide \(a_{15}=80\) mm. Suponemos que el aumento diario es constante, es decir, los datos forman una progresión aritmética.
En una progresión aritmética, el término general es \(a_n=a_1+(n-1)d.\) Aplicamos para \(n=15:\)
\(a_{15}=a_1+14d→80=10+14d\)
Despejamos \(d:\)
\(80-10=14d→70=14d→d=\dfrac{70}{14}=5\)
Por tanto, el tallo creció 5 mm diarios.
Sucesiones geométricas
Ejercicio 1
Determinar la razón, el término general y la monotonía de las siguientes progresiones geométricas:
- 5, 15, 45, 135, 405,...
- -2, -4, -8, -16, -32, …
- 2/3, 2, 6, 18, …
Solución 1
Estudiamos la progresión geométrica 5, 15, 45, 135, 405,...
Para hallar la razón, dividimos un término entre el anterior:
\(r=\dfrac{15}{5}=3,\quad \dfrac{45}{15}=3,\quad \dfrac{135}{45}=3,\quad \dfrac{405}{135}=3\)
La razón es constante e igual a \(r=3.\) El primer término es \(a_1=5.\) El término general de una progresión geométrica es \(a_n=a_1\cdot r^{n-1}.\) Sustituyendo:
\(a_n=5\cdot 3^{n-1}\)
Verificamos para algunos valores: \(n=1\) da \(5\cdot 3^0=5;\) \(n=2\) da \(5\cdot 3^1=15;\) \(n=3\) da \(5\cdot 3^2=45;\) correcto.
En cuanto a la monotonía, observamos que todos los términos son positivos y la razón es \(r=3>1.\) En una progresión geométrica con términos positivos y razón mayor que 1, los términos crecen indefinidamente. Por tanto, la sucesión es creciente (estrictamente).
Solución 2
Consideramos la progresión -2, -4, -8, -16, -32,...
Calculamos la razón dividiendo un término entre el anterior:
\(r=\dfrac{-4}{-2}=2,\quad \dfrac{-8}{-4}=2,\quad \dfrac{-16}{-8}=2,\quad \dfrac{-32}{-16}=2\)
La razón es \(r=2.\) El primer término es \(a_1=-2.\) El término general es:
\(a_n=a_1\cdot r^{n-1}=-2\cdot 2^{n-1}\)
Podemos simplificar: \(a_n=-2^n.\) Verificamos: para \(n=1,\) \(-2^1=-2;\) para \(n=2,\) \(-2^2=-4;\) para \(n=3,\) \(-2^3=-8;\) correcto.
Para analizar la monotonía, observamos que los términos son todos negativos y la razón es \(r=2>1.\) Al multiplicar un número negativo por una razón mayor que 1, obtenemos otro número negativo de mayor valor absoluto, pero más negativo. Por ejemplo, \(-2,-4,-8, \ldots\) Cada término es menor que el anterior (en el orden de los números reales, \(-8<-4<-2\)). Por tanto, la sucesión es decreciente (estrictamente).
Solución 3
Estudiamos la progresión geométrica \(\dfrac{2}{3}, 2, 6, 18, \ldots\)
Para hallar la razón, dividimos un término entre el anterior:
\(r=\dfrac{2}{\dfrac{2}{3}}=2\cdot \dfrac{3}{2}=3,\quad \dfrac{6}{2}=3,\quad \dfrac{18}{6}=3\)
La razón es constante e igual a \(r=3.\) El primer término es \(a_1=\dfrac{2}{3}.\) El término general de una progresión geométrica es \(a_n=a_1\cdot r^{n-1}.\) Sustituyendo:
\(a_n=\dfrac{2}{3}\cdot 3^{n-1}\)
Podemos simplificar: \(a_n=2\cdot 3^{n-2}.\) Verificamos para algunos valores:
\(n=1\) da \(\dfrac{2}{3}\cdot 3^{0}=\dfrac{2}{3}\)
\(n=2\) da \(\dfrac{2}{3}\cdot 3^{1}=2\)
\(n=3\) da \(\dfrac{2}{3}\cdot 3^{2}=\dfrac{2}{3}\cdot 9=6;\) correcto.
En cuanto a la monotonía, observamos que todos los términos son positivos y la razón es \(r=3>1.\) En una progresión geométrica con términos positivos y razón mayor que 1, los términos crecen indefinidamente. Por tanto, la sucesión es creciente (estrictamente).
Ejercicio 2
María quiere comprarse una computadora y ahorra $120 el primer mes y cada mes ahorra el doble de lo ahorrado el mes anterior, ¿cuánto tiene después de cuatro meses?
Solución
Las cantidades mensuales forman una progresión geométrica con primer término \(a_1=120\) y razón \(r=2\)
Queremos saber cuánto tiene después de cuatro meses, es decir, la suma de lo ahorrado durante esos cuatro meses. La suma de los primeros \(n\) términos de una progresión geométrica es:
\(S_n=a_1 \dfrac{r^n-1}{r-1}, \quad \text{para } r ≠ 1\)
Aplicamos con \(n=4:\)
\(S_4=120\cdot \dfrac{2^4-1}{2-1}=120\cdot (16-1)=120\cdot 15=1800\)
Por tanto, después de cuatro meses María tiene $1800.
Ejercicio 3
Un tipo de bacteria se reproduce por bipartición cada media hora. ¿Cuántas bacterias habrá después de 3 horas si inicialmente hay cien bacterias?
Solución
La bacteria se reproduce por bipartición cada media hora. Esto significa que cada 30 minutos el número de bacterias se duplica. Comenzamos con 100 bacterias iniciales. Después de 3 horas, calculamos cuántos períodos de media hora han transcurrido.
3 horas equivalen a \(3 \times 60=180\) minutos. Dividimos entre 30:
\(\dfrac{180}{30}=6 \text{ períodos}\)
Cada período la cantidad se multiplica por 2. Por tanto, al cabo de 6 períodos, el número de bacterias es:
\(N=100\cdot 2^{6}=100\cdot 64=6400\)
Por tanto, después de 3 horas habrá 6400 bacterias.
Ejercicio 4
Un material radioactivo pierde un 0,1% de masa cada año. Si la masa inicial es de 340 g, ¿cuál será su masa dentro de 100 años?
Solución
El material radioactivo pierde un 0,1% de su masa cada año. Esto significa que cada año retiene el 99,9% de la masa del año anterior. La masa sigue una progresión geométrica con razón \(r=1-0,001=0,999.\) La masa inicial es \(a_0=340\) g (consideramos \(a_0\) como la masa en el instante inicial, luego \(a_1\) sería la masa después de 1 año).
Después de \(n\) años, la masa es:
\(a_n=a_0\cdot r^n=340\cdot (0,999)^{100}≈340 \cdot 0,9048=307,632\)
Por tanto, dentro de 100 años la masa será aproximadamente de 307,63 g.
Sucesiones recursivas
Una sucesión recursiva es aquella en la que cada término, después de uno o varios iniciales, se obtiene a partir de los términos que le anteceden a través de una fórmula llamada ley de recurrencia.
Ejercicio 1
Supongamos que los conejos viven por siempre y que cada mes cada par produce un nuevo par que se hace productivo a la edad de 2 meses. Si empezamos con un par recién nacido, ¿cuántos pares de conejos tendremos en el décimo mes?
Solución
Condiciones del problema:
- Cada mes, cada par de conejos productivo (edad ≥ 2 meses) produce un nuevo par.
- Los conejos viven para siempre.
- Empezamos con un par recién nacido (0 meses de edad) en el mes 1.
Construimos una tabla mes a mes.
| Mes | Parejas al inicio del mes | Parejas aptas al inicio del mes | Nuevas parejas que nacen durante el mes | Parejas al final del mes |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 |
| 2 | 1 | 0 | 0 | 1 |
| 3 | 1 | 1 | 1 | 2 |
| 4 | 2 | 1 | 1 | 3 |
| 5 | 3 | 2 | 2 | 5 |
| 6 | 5 | 3 | 3 | 8 |
| 7 | 8 | 5 | 5 | 13 |
| 8 | 13 | 8 | 8 | 21 |
| 9 | 21 | 13 | 13 | 34 |
| 10 | 34 | 21 | 21 | 55 |
En la tabla vemos que el décimo mes tendremos 55 pares de conejos. También observamos que a partir del tercer mes, cada término se obtiene sumando los dos anteriores:
2 = 1 + 1
3 = 2 + 1
5 = 3 + 2
8 = 5 + 3
13 = 8 + 5
…
Esta es la conocida sucesión de Fibonacci, definida por \(F_1=1,\) \(F_2=1\) y \(F_n=F_{n-1}+F_{n-2}\) para \(n ≥ 3.\) El décimo término es \(F_{10}=55.\) De hecho, este mismo problema fue el que dio origen a la sucesión.
Ejercicio 2
Considerar la sucesión \(\sqrt{2}, \sqrt{2+\sqrt{2}}, \sqrt{2+\sqrt{2+\sqrt{2}}}.\)
- Calcula los primeros cinco términos de esta sucesión.
- Escribir la fórmula de recurrencia para an, para n ≥ 2.
- Hallar el límite de la sucesión.
Solución
a) Primeros cinco términos
Calculamos directamente, manteniendo las expresiones radicales y también aproximaciones decimales para visualizar la tendencia.
\(a_1=\sqrt{2}≈1,4142\)
\(a_2=\sqrt{2+\sqrt{2}}≈1,8478\)
\(a_3=\sqrt{2+\sqrt{2+\sqrt{2}}}≈1,9616\)
\(a_4=\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}≈1,9904\)
\(a_5=\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}≈1,9976\)
Observamos que los términos aumentan y se acercan a 2.
b) Fórmula de recurrencia
Observamos la construcción: cada término a partir del segundo se obtiene sumando 2 al término anterior y tomando raíz cuadrada. Es decir, dado \(a_1=\sqrt{2},\) para \(n ≥ 2\) se tiene:
\(a_n=\sqrt{2+a_{n-1}}\)
Esta es la relación de recurrencia que define la sucesión.
c) Límite de la sucesión
Supongamos que la sucesión converge a un límite \(L.\) Entonces, cuando \(n\) tiende a infinito, \(a_n\) y \(a_{n-1}\) tienden ambas a \(L.\) Aplicando la recurrencia en el límite:
\(L=\sqrt{2+L}\)
Elevamos al cuadrado ambos miembros (teniendo en cuenta que \(L\) debe ser positivo por ser límite de términos positivos):
\(L^2=2+L→L^2-L-2=0\)
Resolvemos la ecuación de segundo grado:
\(L=\dfrac{1±\sqrt{1+8}}{2}=\dfrac{1±3}{2}\)
Las soluciones son \(L=\dfrac{1+3}{2}=2\) y \(L=\dfrac{1-3}{2}=-1.\) Descartamos \(L=-1\) por ser negativo (la sucesión es de términos positivos). Por tanto, el límite es \(L=2.\) Esto coincide con las aproximaciones de los términos calculados. Concluimos que la sucesión converge y su límite es 2.
Ejercicio 3
La sucesión de Fibonacci se define recursivamente por:
\(F_1=1, F_2 =1, F_n=F_{n-1}+F_{n-2}~ (n ≥ 3)\)
Sea an la sucesión definida por el cociente entre dos términos consecutivos de Fibonacci, es decir:
\(a_n=\dfrac{F_{n+1}}{F_n},\quad n ≥ 1\)
Analizar si la sucesión an es convergente y encontrar el valor de su límite.
Solución
Sabemos que \(F_{n+1}=F_n+F_{n-1}.\) Dividimos ambos miembros entre \(F_n:\)
\(\dfrac{F_{n+1}}{F_n}=1+\dfrac{F_{n-1}}{F_n}\)
Pero \(\dfrac{F_{n-1}}{F_n}=\dfrac{1}{F_n / F_{n-1}}=\dfrac{1}{a_{n-1}}.\) Por tanto:
\(a_n=1+\dfrac{1}{a_{n-1}}\)
Esta es la relación de recurrencia para \(a_n,\) válida para \(n ≥ 2.\)
Para estudiar la monotonía y acotación, primero calculamos los primeros términos:
\(a_1=\dfrac{F_2}{F_1}=\dfrac{1}{1}=1\)
\(a_2=\dfrac{F_3}{F_2}=\dfrac{2}{1}=2\)
\(a_3=\dfrac{F_4}{F_3}=\dfrac{3}{2}=1,5\)
\(a_4=\dfrac{F_5}{F_4}=\dfrac{5}{3}≈1,6667\)
\(a_5=\dfrac{F_6}{F_5}=\dfrac{8}{5}=1,6\)
\(a_6=\dfrac{F_7}{F_6}=\dfrac{13}{8}=1,625\)
Observamos que la sucesión oscila alrededor de un valor, pero parece que se estabiliza. Se puede demostrar que \(a_n\) está acotada entre 1 y 2 (por ejemplo, por inducción) y que es una sucesión que alterna: \(a_{2k}\) decrece, \(a_{2k+1}\) crece, y ambas subsucesiones convergen al mismo límite.
Cálculo del límite
Supongamos que \(\lim_{n→\infty} a_n=L.\) Aplicamos el límite a la recurrencia \(a_n=1+\dfrac{1}{a_{n-1}}:\)
\(L=1+\dfrac{1}{L}\)
Multiplicamos por \(L:\)
\(L^2=L+1→L^2-L-1=0\)
Resolvemos:
\(L=\dfrac{1±\sqrt{1+4}}{2}=\dfrac{1±\sqrt{5}}{2}\)
Como \(a_n>0,\) tomamos la raíz positiva:
\(L=\dfrac{1+\sqrt{5}}{2}\)
Este número es la conocida razón áurea \(\varphi≈1,6180,\) muy presente en la naturaleza y en la arquitectura, entre otros contextos.
Problemas de la vida real
Los siguientes problemas consisten en algunos usos de las sucesiones numéricas en la vida cotidiana.
Ejercicio 1: Interés compuesto
Juan deposita $2000 en una cuenta de ahorros que paga 2,4% de interés al año capitalizado mensualmente.
- Encontrar una fórmula que diga la cantidad en cuenta después de n meses.
- Calcular la cantidad de dinero después de 3 años.
Solución
a) Necesitamos modelar el crecimiento del dinero mediante interés compuesto. El depósito inicial es 2000 dólares y la tasa anual es del 2,4%, pero como se capitaliza mensualmente debemos trabajar con la tasa mensual. Dividimos la tasa anual entre 12: 2,4% / 12 = 0,2% mensual, que en forma decimal es 0,002. Cada mes el capital se multiplica por 1 + 0,002 = 1,002. Después de n meses, la cantidad acumulada es:
\(A_n=2000\cdot (1,002)^n\)
Esta es la fórmula buscada.
b) Ahora calculamos la cantidad después de 3 años, que equivalen a \(n=36\) meses:
\(A_{36}=2000\cdot (1,002)^{36}≈2000\cdot 1,0746=2149,20\)
Por lo tanto, después de 3 años hay unos \(2149,20\) dólares.
Ejercicio 2: Población de una ciudad
En el año 2004, una ciudad tenía una población de 35 000. Se espera que la población aumente a razón de 2% al año.
- Obtener una fórmula para la población n años después de 2004.
- ¿De cuánto sería la población en 2024?
Solución
La población inicial en 2004 es 35 000 y crece un 2% anual. Un aumento del 2% significa multiplicar por \(1+\dfrac{2}{100}=1,02\) cada año. Si n representa los años transcurridos desde 2004, la población al cabo de n años es:
\(P_n=35\,000\cdot (1,02)^n\)
Para 2024 han pasado n = 2024 - 2004 = 20 años. Sustituimos:
\(P_{20}=35\,000\cdot (1,02)^{20}≈35\,000\cdot 1,4859=52\,006,50\)
La población estimada en 2024 es de 52 007 habitantes.
Ejercicio 3: Inflación
La proporción de inflación es de 5% por año y el precio medio de un automóvil es actualmente $25 000.
- Encontrar una fórmula para el precio medio después de n años.
- Calcular los precios medios durante los próximos 5 años.
Solución
a) El precio medio actual del automóvil es 25 000 dólares y la inflación anual es del 5%, lo que significa que cada año el precio se multiplica por 1,05. Después de n años, el precio medio será:
\(P_n=25\,000\cdot (1,05)^n\)
b) Para los próximos 5 años, calculamos P1, P2, P3, P4, P5:
\(P_1=25\,000\cdot (1,05)^1=26\,250\)
\(P_2=25\,000\cdot (1,05)^2=27\,562,50\)
\(P_3=25\,000\cdot (1,05)^3≈28\,940,63\)
\(P_4=25\,000\cdot (1,05)^4≈30\,387,66\)
\(P_5=25\,000\cdot (1,05)^5≈31\,907,04\)
Ejercicio 4: Gastos gubernamentales
Un programa de gobierno que actualmente cuesta $4,5 mil millones por año, se va a reducir 20% por año.
- Escribir una expresión para la cantidad presupuestada para este programa después de n años.
- Calcular los presupuestos durante los primeros 4 años.
- Determinar la convergencia o divergencia de la sucesión de presupuestos reducidos. Si la sucesión converge, encontrar su límite.
Solución
a) El gasto inicial del programa es 4,5 mil millones de dólares y se reduce un 20% anual. Una reducción del 20% significa que cada año se conserva el 80% del año anterior, es decir, se multiplica por 0,8. Después de n años, el presupuesto será:
\(G_n=4,5\cdot (0,8)^n \quad \text{(en miles de millones de dólares)}\)
b) Tomando \(G_0=4,5\) como el gasto actual, calculamos los primeros 4 años:
\(G_1=4,5\cdot 0,8=3,6\)
\(G_2=4,5\cdot (0,8)^2=2,88\)
\(G_3=4,5\cdot (0,8)^3=2,304\)
\(G_4=4,5\cdot (0,8)^4=1,8432\)
Estos valores están en miles de millones de dólares.
c) La sucesión es geométrica con razón r = 0,8, que tiene valor absoluto menor que 1, por lo tanto la sucesión converge a 0. El límite cuando \(n → ∞\) es:
\(\lim_{n→\infty} G_n=\lim_{n→\infty} 4,5\cdot (0,8)^n=0\)
Es decir, el presupuesto tiende a cero con el paso de los años.
Ejercicio 5: Sueldo de un empleado
Una empresa ofrece a un empleado un sueldo de $1000 y una subida de $100 al año. Otra le ofrece el mismo sueldo con una subida del 10% anual. Determinar cuál de las dos es mejor comparando el sueldo dentro de 10 años.
Solución
Analizamos las dos ofertas por separado. En la primera, el sueldo inicial es 1000 dólares y aumenta 100 dólares cada año. Esto corresponde a una progresión aritmética. El sueldo después de n años es:
\(S_n^{\text{(arit)}}=1000+100n\)
Para n = 10:
\(S_{10}^{\text{(arit)}}=1000+100\cdot 10=2000\)
En la segunda oferta, el sueldo inicial es también 1000 pero aumenta un 10% anual, lo que significa una progresión geométrica con razón 1,10. El sueldo después de n años es:
\(S_n^{\text{(geom)}}=1000\cdot (1,1)^n\)
Para n = 10:
\(S_{10}^{\text{(geom)}}=1000\cdot (1,1)^{10}≈2593,74\)
Comparando ambos resultados, el sueldo con aumento del 10% anual (2593,74 dólares) es superior al sueldo con aumento fijo de 100 dólares anuales (2000 dólares). Por tanto, a largo plazo resulta mejor la opción del aumento porcentual.
Bibliografía
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2026, 20 de febrero). Ejercicios resueltos de sucesiones numéricas. Dexmath. https://dexmath.com/ejercicios-sucesiones
Deja una respuesta

Otros artículos que pueden interesarte