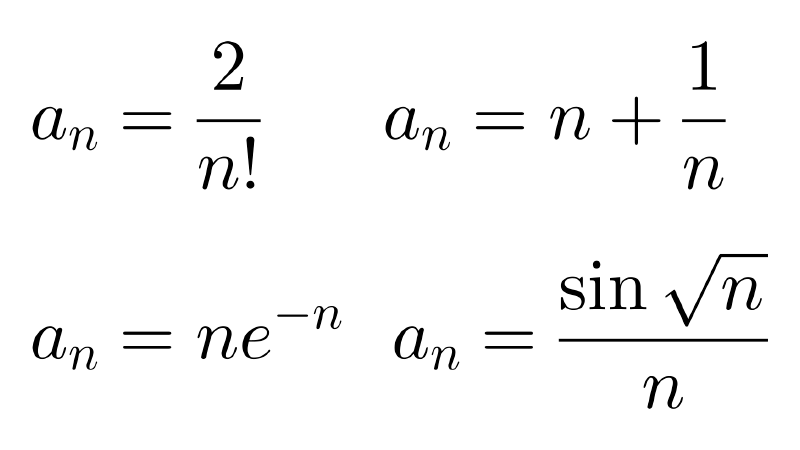
Término general de una sucesión
El término general de una sucesión es una fórmula que nos permite obtener cualquier término de la sucesión a partir de su posición en la secuencia. Se representa generalmente como an y se llama "enésimo término".
Por ejemplo:
- \(a_n=2n\) es el término general de la sucesión de números pares (2, 4, 6, 8, 10, …).
- \(a_n=\dfrac{1}{n}\) es una fórmula para la secuencia de fracciones \((a_n)=\left(1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, …\right).\)
- \(c_n=2n-1\) es un término general que define la sucesión de números impares \((c_n)=(1, 3, 5, 7, 9, 11, …).\)
- El término \(d_n=3+(-1)^n\) genera la secuencia (2, 4, 2, 4, 2, 4, …).
No todas las sucesiones pueden tener un término general, por ejemplo, para la sucesión de números primos (2, 3, 5, 7, 11, 13, 17, 19, 23, …) no existe una fórmula conocida que permita obtener el n-ésimo término.
El término general de una sucesión sirve, principalmente, para calcular cualquier término sin tener que conocer los anteriores. Además, permite analizar el comportamiento de la sucesión, como si crece, decrece o se estabiliza, y estudiar su convergencia mediante el cálculo de límites.
Índice
Cómo calcular el término general
Para encontrar el término general, tenemos que buscar el patrón o regla que relacione el valor de cada término con su posición en la sucesión y expresarlo como una fórmula.
Estos son los pasos que podemos seguir para hallar la fórmula general:
- Comprobar si se trata de una progresión aritmética: para esto, restamos pares de términos consecutivos; si la diferencia es constante, se trata de una secuencia aritmética, y su término general tiene la forma an = a1 + (n - 1) ⋅ d, donde a1 es el primer término y d es la diferencia común.
- Comprobar si se trata de una progresión geométrica: dividimos pares de términos consecutivos; si el cociente es constante, es una sucesión geométrica y su término general tiene la forma an = a1 ⋅ rn-1 donde a1 es el primer término y r es el cociente común, llamado razón.
- Comprobar si es una sucesión conocida: verificamos si es una secuencia de potencias perfectas como cuadrados o cubos o números muy cercanos a esos.
- Detectar cambios de signo: si los términos cambian de signo alternativamente, el término general debe ser multiplicado por la forma (-1)n o (-1)n+1, dependiendo de cuál se ajuste a la secuencia.
- Sucesiones de fracciones: si los términos de la sucesión son fraccionarios, debemos hallar la fórmula general del numerador y del denominador por separado y luego formar la fracción.
Es recomendable probar si el término general hallado es correcto calculando con él los primeros términos de la sucesión y viendo si coinciden con los dados por el problema. También puedes usar esta herramienta online para validar tus resultados:
Ejercicios resueltos
Sucesiones de números enteros
Calcular el término general de las siguientes sucesiones dados sus primeros términos.
- 3, 8, 13, 18, 23, …
- -3, -1, 1, 3, 5, 7, …
- 1, -1, 1, -1, …
- 1, 2, 4, 8, 16, …
- 5, 15, 45, 135, …
- -2, 4, -8, 16, …
- 1, 4, 9, 16, …
- 1, 3, 6, 10, …
- 1, 8, 27, 64, …
- -2, -5, -10, -17, …
- 2, 6, 12, 20, …
- 0, 3, 8, 15, …
- 5, 10, 17, 26, 37, …
- 3, 6, 11, 18, …
- 1, 2, 4, 7, 11, …
Soluciones
Solución 1
Para calcular el término general de la sucesión dada 3, 8, 13, 18, 23, …, primero observamos la diferencia entre términos consecutivos. Al restar cada término con su anterior, obtenemos:
\(8-3=5\)
\(13-8=5\)
\(18-13=5\)
\(23-18=5\)
Vemos que la diferencia es constante e igual a 5, lo que indica que se trata de una sucesión aritmética.
En una sucesión aritmética, el término general \(a_n\) se expresa como:
\(a_n=a_1+(n-1) \cdot d\)
donde \(a_1\) es el primer término y \(d\) es la diferencia común. En este caso, \(a_1=3\) y \(d=5.\) Sustituyendo estos valores, obtenemos:
\(a_n=3+(n-1) \cdot 5\)
Simplificando la expresión:
\(a_n=3+5n-5\)
\(a_n=5n-2\)
Para verificar la fórmula, probamos con los primeros cuatro términos:
Para \(n=1\): \(a_1=5(1)-2=3\)
Para \(n=2\): \(a_2=5(2)-2=8\)
Para \(n=3\): \(a_3=5(3)-2=13\)
Para \(n=4\): \(a_4=5(4)-2=18\)
La fórmula \(a_n=5n-2\) genera correctamente los términos de la sucesión.
Solución 2
En la secuencia -3, -1, 1, 3, 5, 7, … comenzamos analizando las diferencias entre términos consecutivos. Al restar cada término con su anterior, obtenemos:
\(-1-(-3)=2, \quad 1-(-1)=2, \quad 3-1=2, \quad 5-3=2, \quad 7-5=2\)
La diferencia es constante e igual a \(2,\) lo que confirma que es una sucesión aritmética.
En una sucesión aritmética, el término general \(a_n\) se expresa como:
\(a_n=a_1+(n-1) \cdot d\)
donde \(a_1\) es el primer término y \(d\) es la diferencia común. En este caso, \(a_1=-3\) y \(d=2.\) Sustituyendo estos valores, obtenemos:
\(a_n=-3+(n-1) \cdot 2\)
Simplificando la expresión:
\(a_n=-3+2n-2=2n-5\)
Para verificar la fórmula, probamos con los primeros cuatro términos:
Para \(n=1\): \(a_1=2(1)-5=-3,\)
Para \(n=2\): \(a_2=2(2)-5=-1,\)
Para \(n=3\): \(a_3=2(3)-5=1,\)
Para \(n=4\): \(a_4=2(4)-5=3.\)
La fórmula \(a_n=2n-5\) genera correctamente los términos de la sucesión.
Solución 3
La sucesión 1, -1, 1, -1, … alterna entre 1 y -1. Este comportamiento periódico sugiere una dependencia de \((-1)^{n+1}\) o similar.
Proponemos el término general:
\(a_n=(-1)^{n+1}\)
Verificación:
Para \(n=1\): \(a_1=(-1)^{2}=1\)
Para \(n=2\): \(a_2=(-1)^{3}=-1\)
Para \(n=3\): \(a_3=(-1)^{4}=1\)
La fórmula \(a_n=(-1)^{n+1}\) reproduce la sucesión.
Solución 4
La sucesión 1, 2, 4, 8, 16, … muestra que cada término es el doble del anterior. Esto indica una progresión geométrica con razón \(r=2.\)
El término general de una sucesión geométrica es:
\(a_n=a_1 \cdot r^{n-1}\)
Con \(a_1=1\) y \(r=2:\)
\(a_n=1 \cdot 2^{n-1}=2^{n-1}\)
Verificación:
Para \(n=1\): \(a_1=2^{0}=1\)
Para \(n=2\): \(a_2=2^{1}=2\)
Para \(n=3\): \(a_3=2^{2}=4\)
La fórmula \(a_n=2^{n-1}\) es válida.
Solución 5
La sucesión 5, 15, 45, 135, … evidencia que cada término se multiplica por 3 respecto al anterior (\(r=3\)). Es una progresión geométrica.
Aplicando la fórmula \(a_n=a_1 \cdot r^{n-1},\) con \(a_1=5\) y \(r=3:\)
\(a_n=5 \cdot 3^{n-1}\)
Verificación:
Para \(n=1\): \(a_1=5 \cdot 3^{0}=5\)
Para \(n=2\): \(a_2=5 \cdot 3^{1}=15\)
Para \(n=3\): \(a_3=5 \cdot 3^{2}=45\)
La fórmula \(a_n=5 \cdot 3^{n-1}\) es correcta.
Solución 6
La sucesión -2, 4, -8, 16, … combina un cambio de signo alternado con una duplicación en valor absoluto. Esto sugiere una progresión geométrica con razón \(r=-2.\)
Usando \(a_n=a_1 \cdot r^{n-1},\) con \(a_1=-2\) y \(r=-2:\)
\(a_n=-2 \cdot (-2)^{n-1}\)
Simplificando:
\(a_n=(-2)^1 \cdot (-2)^{n-1}=(-2)^n\)
Verificación:
Para \(n=1\): \(a_1=(-2)^1=-2\)
Para \(n=2\): \(a_2=(-2)^2=4\)
Para \(n=3\): \(a_3=(-2)^3=-8\)
La fórmula \(a_n=(-2)^n\) describe la sucesión.
Solución 7
La sucesión dada es 1, 4, 9, 16,... Observamos que estos términos corresponden a los cuadrados de los números naturales:
\(1=1^2, \quad 4=2^2, \quad 9=3^2, \quad 16=4^2\)
Por lo tanto, el término general \(a_n\) se puede expresar como:
\(a_n=n^2\)
Verificamos la fórmula con los primeros términos:
Para \(n=1\): \(a_1=1^2=1,\)
Para \(n=2\): \(a_2=2^2=4,\)
Para \(n=3\): \(a_3=3^2=9.\)
La fórmula \(a_n=n^2\) genera correctamente la sucesión.
Solución 8
La sucesión 1, 3, 6, 10,... presenta diferencias consecutivas no constantes pero con un patrón reconocible. Calculamos las diferencias entre términos:
\(3-1=2, \quad 6-3=3, \quad 10-6=4\)
Las diferencias aumentan en \(1\) cada vez, lo que sugiere una relación con los números triangulares. El término general de los números triangulares es:
\(a_n=\dfrac{n(n+1)}{2}\)
Verificamos la fórmula:
Para \(n=1\): \(a_1=\dfrac{1 \cdot 2}{2}=1,\)
Para \(n=2\): \(a_2=\dfrac{2 \cdot 3}{2}=3,\)
Para \(n=3\): \(a_3=\dfrac{3 \cdot 4}{2}=6.\)
La fórmula \(a_n=\dfrac{n(n+1)}{2}\) es correcta.
Solución 9
La sucesión 1, 8, 27, 64,... está formada por los cubos de los números naturales:
\(1=1^3, \quad 8=2^3, \quad 27=3^3, \quad 64=4^3\)
Así, el término general es:
\(a_n=n^3\)
Comprobamos:
Para \(n=1\): \(a_1=1^3=1,\)
Para \(n=2\): \(a_2=2^3=8,\)
Para \(n=3\): \(a_3=3^3=27.\)
La fórmula \(a_n=n^3\) reproduce la sucesión.
Solución 10
La sucesión negativa -2, -5, -10, -17,... muestra términos que siguen un patrón cuadrático. Analizamos su comportamiento:
\(-2=-(1^2+1)\)
\(-5=-(2^2+1)\)
\(-10=-(3^2+1)\)
\(-17=-(4^2+1)\)
Esto sugiere que el término general es:
\(a_n=-(n^2+1)\)
Verificación:
Para \(n=1\): \(a_1=-(1+1)=-2,\)
Para \(n=2\): \(a_2=-(4+1)=-5,\)
Para \(n=3\): \(a_3=-(9+1)=-10.\)
La fórmula \(a_n=-(n^2+1)\) es válida.
Solución 11
La sucesión 2, 6, 12, 20,... presenta el producto de números enteros consecutivos. Observamos:
\(2=1 \times 2\)
\(6=2 \times 3\)
\(12=3 \times 4\)
\(20=4 \times 5\)
Por lo tanto, el término general es:
\(a_n=n(n+1)\)
Comprobamos:
Para \(n=1\): \(a_1=1 \times 2=2,\)
Para \(n=2\): \(a_2=2 \times 3=6,\)
Para \(n=3\): \(a_3=3 \times 4=12.\)
La fórmula \(a_n=n(n+1)\) genera la sucesión correctamente.
Solución 12
La sucesión 0, 3, 8, 15,... puede analizarse restando cada término con su anterior:
\(3-0=3, \quad 8-3=5, \quad 15-8=7\)
Las diferencias son \(3, 5, 7,...,\) una sucesión aritmética con diferencia \(2.\) Esto sugiere una relación cuadrática. Observamos que los términos coinciden con \(n^2-1:\)
\(0=1^2-1, \quad 3=2^2-1, \quad 8=3^2-1, \quad 15=4^2-1\)
Por lo tanto, el término general es:
\(a_n=n^2-1\)
Verificación:
Para \(n=1\): \(a_1=1-1=0,\)
Para \(n=2\): \(a_2=4-1=3,\)
Para \(n=3\): \(a_3=9-1=8.\)
La fórmula \(a_n=n^2-1\) es correcta.
Solución 13
La sucesión 5, 10, 17, 26, 37,... muestra diferencias consecutivas crecientes:
\(10-5=5, \quad 17-10=7, \quad 26-17=9, \quad 37-26=11\)
Las diferencias (\(5, 7, 9, 11,...\)) aumentan en \(2,\) lo que indica un comportamiento cuadrático. Buscamos un patrón similar a \(n^2+\text{algo}.\) Notamos que:
\(5=2^2+1, \quad 10=3^2+1, \quad 17=4^2+1, \quad 26=5^2+1\)
Por lo tanto, el término general es:
\(a_n=(n+1)^2+1=n^2+2n+2\)
Verificación:
Para \(n=1\): \(a_1=1+2+2=5,\)
Para \(n=2\): \(a_2=4+4+2=10,\)
Para \(n=3\): \(a_3=9+6+2=17.\)
La fórmula \(a_n=n^2+2n+2\) genera la sucesión.
Solución 14
La sucesión 3, 6, 11, 18,... tiene diferencias:
\(6-3=3, \quad 11-6=5, \quad 18-11=7\)
Las diferencias (\(3, 5, 7,...\)) son impares consecutivos, lo que sugiere una relación cuadrática. Observamos que:
\(3=1^2+2, \quad 6=2^2+2, \quad 11=3^2+2, \quad 18=4^2+2\)
Así, el término general es:
\(a_n=n^2+2\)
Verificación:
Para \(n=1\): \(a_1=1+2=3,\)
Para \(n=2\): \(a_2=4+2=6,\)
Para \(n=3\): \(a_3=9+2=11.\)
La fórmula \(a_n=n^2+2\) es válida.
Solución 15
La sucesión 1, 2, 4, 7, 11,... tiene diferencias:
\(2-1=1, \quad 4-2=2, \quad 7-4=3, \quad 11-7=4\)
Las diferencias aumentan en \(1,\) lo que sugiere una relación cuadrática. Esta sucesión corresponde a los números triangulares desplazados:
\(1=1, \quad 2=1+1, \quad 4=1+2+1, \quad 7=1+2+3+1\)
El término general es:
\(a_n=1+\dfrac{n(n-1)}{2}\)
Verificación:
Para \(n=1\): \(a_1=1+0=1,\)
Para \(n=2\): \(a_2=1+1=2,\)
Para \(n=3\): \(a_3=1+3=4.\)
La fórmula \(a_n=1+\dfrac{n(n-1)}{2}\) genera la sucesión.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Sucesiones de fracciones
Hallar el término general de las siguientes sucesiones con fracciones dados sus primeros términos:
- \(1, \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \dfrac{1}{16}\)
- \(\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{6}, \dfrac{7}{8}, …\)
- \(1, \dfrac{2}{3}, \dfrac{3}{5}, \dfrac{4}{7}, \dfrac{5}{9}, …\)
- \(0, \dfrac{1}{4}, \dfrac{2}{9}, \dfrac{3}{16}, …\)
- \(-1, \dfrac{1}{2}, -\dfrac{1}{3}, \dfrac{1}{4}, -\dfrac{1}{5},...\)
- \(-\dfrac{1}{2}, \dfrac{1}{5}, \dfrac{3}{8}, \dfrac{5}{11},...\)
- \(\dfrac{3}{5}, -\dfrac{4}{25}, \dfrac{5}{125}, -\dfrac{6}{625}, \dfrac{7}{3125}, …\)
- \(\dfrac{3}{4}, \dfrac{6}{9}, \dfrac{9}{16}, \dfrac{12}{25}, \dfrac{5}{36}, \dfrac{18}{49}, …\)
Soluciones
Solución 1
Para hallar el término general de la sucesión dada \(1, \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \dfrac{1}{16}, \ldots,\) observamos que cada término parece ser una fracción cuyo numerador es siempre 1 y cuyo denominador sigue un patrón específico.
Analizando los términos:
\(a_1=1=\dfrac{1}{2^0}\)
\(a_2=\dfrac{1}{2}=\dfrac{1}{2^1}\)
\(a_3=\dfrac{1}{4}=\dfrac{1}{2^2}\)
\(a_4=\dfrac{1}{8}=\dfrac{1}{2^3}\)
Se deduce que el denominador del n-ésimo término sigue la potencia de 2 con exponente \(n-1.\) Por lo tanto, el término general \(a_n\) de la sucesión puede expresarse como:
\(a_n=\dfrac{1}{2^{n-1}}\)
Se trata de una progresión geométrica decreciente de razón \(\dfrac{1}{2}\) y primer término \(1.\)
Solución 2
La sucesión dada es \(\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{6}, \dfrac{7}{8}, \ldots,\) analizamos por separado los numeradores y denominadores.
Los numeradores son \(1, 3, 5, 7, \ldots,\) que corresponden a los números impares. El n-ésimo número impar puede expresarse como \(2n-1.\) Por otro lado, los denominadores son \(2, 4, 6, 8, \ldots,\) que son los números pares, y su n-ésimo término es \(2n.\)
Combinando ambas observaciones, el término general \(a_n\) de la sucesión queda definido como:
\(a_n=\dfrac{2n-1}{2n}\)
Solución 3
La sucesión dada es \(1, \dfrac{2}{3}, \dfrac{3}{5}, \dfrac{4}{7}, \dfrac{5}{9}, \ldots.\) Al examinar los numeradores y denominadores por separado, identificamos lo siguiente:
Los numeradores siguen la secuencia \(1, 2, 3, 4, 5, \ldots,\) que claramente corresponde a \(n.\) Los denominadores son \(1, 3, 5, 7, 9, \ldots,\) los números impares, cuyo n-ésimo término es \(2n-1.\)
Por lo tanto, el término general \(a_n\) de esta sucesión es:
\(a_n=\dfrac{n}{2n-1}\)
Solución 4
La sucesión \(0, \dfrac{1}{4}, \dfrac{2}{9}, \dfrac{3}{16}, \ldots\) muestra un patrón donde los numeradores aumentan linealmente y los denominadores son cuadrados perfectos.
Los numeradores son \(0, 1, 2, 3, \ldots,\) que pueden expresarse como \(n-1\) (para \(n \geq 1\)). Los denominadores son \(1, 4, 9, 16, \ldots,\) es decir, los cuadrados de los números naturales: \(n^2.\)
Así, el término general \(a_n\) de esta sucesión está dado por:
\(a_n=\dfrac{n-1}{n^2}\)
Solución 5
La sucesión dada es \(-1, \dfrac{1}{2},-\dfrac{1}{3}, \dfrac{1}{4},-\dfrac{1}{5}, \ldots.\) Observamos que los términos alternan en signo y que los denominadores aumentan de manera lineal, mientras que los numeradores son siempre 1 (en valor absoluto).
Para expresar la alternancia de signos, utilizamos \((-1)^n.\) El denominador del n-ésimo término es simplemente \(n.\) Por lo tanto, el término general \(a_n\) se puede escribir como:
\(a_n=(-1)^n \cdot \dfrac{1}{n}\)
Solución 6
La sucesión dada es \(-\dfrac{1}{2}, \dfrac{1}{5}, \dfrac{3}{8}, \dfrac{5}{11}, \ldots.\) Analizaremos por separado los numeradores y denominadores para encontrar el término general.
Los numeradores son \(-1, 1, 3, 5, \ldots,\) que corresponden a una progresión aritmética donde cada término aumenta en \(2.\) El primer término es \(-1\) y la diferencia común es \(2,\) por lo que el n-ésimo numerador puede expresarse como \(2n-3\) (para \(n \geq 1\)).
Los denominadores son \(2, 5, 8, 11, \ldots,\) otra progresión aritmética con primer término \(2\) y diferencia común \(3.\) Así, el n-ésimo denominador es \(3n-1.\)
Combinando ambas expresiones, el término general \(a_n\) de la sucesión es:
\(a_n=\dfrac{2n-3}{3n-1}\)
Solución 7
La sucesión dada es \(\dfrac{3}{5},-\dfrac{4}{25}, \dfrac{5}{125},-\dfrac{6}{625}, \dfrac{7}{3125}, \ldots.\) Observamos que los signos alternan entre positivo y negativo, y los numeradores y denominadores siguen patrones distintos.
Los numeradores son \(3,-4, 5,-6, 7, \ldots.\) Notamos que los valores absolutos aumentan en \(1\) y el signo alterna. Esto puede expresarse como \((-1)^{n+1} \cdot (n+2)\) (para \(n \geq 1\)), donde \((-1)^{n+1}\) maneja la alternancia.
Los denominadores son \(5, 25, 125, 625, 3125, \ldots,\) que son potencias de \(5\): \(5^1, 5^2, 5^3, \ldots.\) Por lo tanto, el n-ésimo denominador es \(5^n.\)
Así, el término general \(a_n\) de la sucesión es:
\(a_n=\dfrac{(-1)^{n+1} \cdot (n+2)}{5^n}\)
Solución 8
La sucesión fraccionaria dada es \(\dfrac{3}{4}, \dfrac{6}{9}, \dfrac{9}{16}, \dfrac{12}{25}, \dfrac{15}{36}, \dfrac{18}{49}, \ldots.\) Analizaremos los numeradores y denominadores por separado para identificar el patrón.
La secuencia de numeradores es \(3, 6, 9, 12, 15, 18, \ldots.\) Observamos que cada término aumenta en \(3,\) lo que corresponde a una progresión aritmética con primer término \(3\) y diferencia común \(3.\) Por lo tanto, el n-ésimo numerador se expresa como \(3n.\)
Los denominadores son \(4, 9, 16, 25, 36, 49, \ldots,\) que son cuadrados perfectos de los números naturales empezando desde \(2:\)
\(2^2, 3^2, 4^2, 5^2, 6^2, 7^2, \ldots\)
Así, el n-ésimo denominador es \((n+1)^2.\)
Combinando ambas expresiones, el término general \(a_n\) de la sucesión es:
\(a_n=\dfrac{3n}{(n+1)^2}\)
Verificación:
Para \(n=1\): \(\dfrac{3 \cdot 1}{(1+1)^2}=\dfrac{3}{4}.\)
Para \(n=2\): \(\dfrac{6}{(2+1)^2}=\dfrac{6}{9}.\)
Para \(n=3\): \(\dfrac{9}{16}.\)
Para \(n=4\): \(\dfrac{12}{25}.\)
Para \(n=5\): \(\dfrac{15}{36}.\)
Para \(n=6\): \(\dfrac{18}{49}.\)
Todos coinciden con los términos dados, confirmando que la fórmula es correcta.
Bibliografía
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

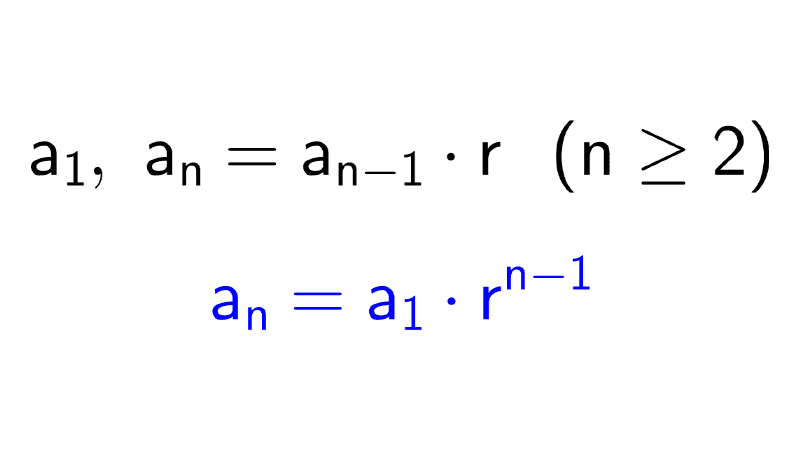
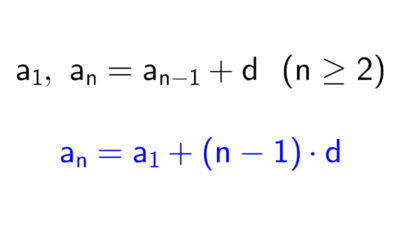
Otros artículos que pueden interesarte