Sucesiones recursivas
Una sucesión recursiva o recurrente es aquella en la que cada término, después de uno o varios iniciales, se obtiene a partir de los términos que le anteceden. A diferencia de una sucesión definida por una fórmula directa, donde se puede calcular cualquier elemento de forma independiente, aquí el avance requiere conocer los valores previos.
Para definir completamente una sucesión de este tipo, se requieren dos elementos fundamentales:
- El término o términos iniciales: son los primeros valores de la sucesión, que sirven como punto de partida para aplicar la regla, también se llaman "condiciones iniciales".
- La relación de recurrencia: es una fórmula que establece cómo se calcula cada nuevo término en función de uno o más de los términos que le preceden inmediatamente.
Índice
Ejemplos
A continuación, veremos algunos ejemplos concretos de sucesiones definidas por recurrencia.
La sucesión de Fibonacci
Esta sucesión es, sin duda, el ejemplo más famoso de sucesión recursiva. Se define típicamente con los dos primeros términos y una regla que relaciona cada término con los dos inmediatamente anteriores.
- Términos iniciales: F1 = 1, F2 = 1
- Relación de recurrencia: Fn = Fn-1 + Fn-2, para n ≥ 3
Esto significa que cada término, a partir del tercero, es la suma de los dos que le preceden. Podemos calcular los primeros términos aplicando la regla:
\(F_3=F_2+F_1=1+1=2\)
\(F_4=F_3+F_2=2+1=3\)
\(F_5=F_4+F_3=3+2=5\)
Por lo tanto, la sucesión comienza así: 1, 1, 2, 3, 5, 8, 13, 21... Esta sucesión aparece en contextos muy diversos, como el crecimiento de poblaciones en biología y patrones en la naturaleza.
Sucesiones aritméticas
Las sucesiones aritméticas son aquellas en las que cada término se obtiene sumando una cantidad constante (llamada diferencia) al término anterior. Es decir, tenemos:
- Término inicial: a1 = k (un valor cualquiera, por ejemplo, a1 = 5)
- Regla recursiva: an = an-1 + d, para n ≥ 2
Por ejemplo, si elegimos \(a_1=5\) y una diferencia \(d=4,\) los términos se calculan así:
\(a_2=a_1+4=5+4=9\)
\(a_3=a_2+4=9+4=13\)
\(a_4=a_3+4=13+4=17\)
La sucesión generada es 5, 9, 13, 17..., avanzando de 4 en 4 a partir del término inicial.
Sucesiones geométricas
Las sucesiones geométricas son aquellas en las que cada término se obtiene multiplicando el término anterior por una cantidad fija (la razón). Es decir:
- Término inicial: a1 = k (por ejemplo, a1 = 2)
- Relación de recursividad: an = r ⋅ an-1, para n ≥ 2
Por ejemplo, si tomamos \(a_1=3\) y una razón \(r=2,\) obtenemos:
\(a_2=2 \cdot a_1=2 \cdot 3=6\)
\(a_3=2 \cdot a_2=2 \cdot 6=12\)
\(a_4=2 \cdot a_3=2 \cdot 12=24\)
La sucesión resultante es 3, 6, 12, 24..., que comienza en 3 y cada término se obtiene multiplicando el anterior por 2.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
La sucesión factorial
El factorial, fundamental en combinatoria y análisis matemático, se obtiene multiplicando todos los números enteros positivos desde 1 hasta un número dado n. Se puede definir de forma recursiva de la siguiente manera:
- Condición inicial: a1 = 1
- Regla de recurrencia: an = n ⋅ an-1, para n ≥ 2
La clave aquí es que la regla de recurrencia depende directamente del índice \(n\) del término que se quiere calcular. Veamos cómo se construyen los primeros términos:
\(a_2=2 \cdot a_1=2 \cdot 1=2\)
\(a_3=3 \cdot a_2=3 \cdot 2=6\)
\(a_4=4 \cdot a_3=4 \cdot 6=24\)
Así, la sucesión factorial comienza con 1, 2, 6, 24, 120..., donde cada término representa el producto de todos los enteros positivos menores o iguales a n.
Tipos de sucesiones recurrentes
Las sucesiones definidas recursivamente pueden clasificarse de diferentes maneras, pero las más comunes son según su orden y según la forma de la relación de recurrencia.
Según el orden
El orden de una sucesión recursiva es el número de términos anteriores necesarios para calcular el término enésimo.
- Sucesiones de primer orden: son las más simples, para calcular \(a_n\) solo se necesita conocer el término inmediatamente anterior, \(a_{n-1}.\) La relación de recurrencia tiene la forma general \(a_n=f(a_{n-1}),\) donde f es una función que define la regla. Los ejemplos más claros son las sucesiones aritméticas (\(a_n=a_{n-1}+d\)) y las sucesiones geométricas (\(a_n=r \cdot a_{n-1}\)).
- Sucesiones de segundo orden: en este caso, el cálculo de \(a_n\) depende de los dos términos que le preceden, \(a_{n-1}\) y \(a_{n-2}.\) La fórmula general es \(a_n=f(a_{n-1}, a_{n-2}).\) El ejemplo por excelencia es la sucesión de Fibonacci (\(F_n=F_{n-1}+F_{n-2}\)).
- Sucesiones de orden k: de forma general, una sucesión es de orden k si para definir \(a_n\) se necesitan los k términos anteriores: \(a_{n-1}, a_{n-2},..., a_{n-k}.\) La relación de recurrencia se expresa como \(a_n=f(a_{n-1}, a_{n-2},..., a_{n-k}).\) Naturalmente, para poder comenzar a aplicar la regla, se deben conocer los k primeros términos o valores iniciales.
Según la forma de la relación
Otra forma de clasificar las sucesiones recursivas es atendiendo a la naturaleza de la función f que define la regla de recurrencia. Según esto, las principales categorías son las sucesiones lineales y las no lineales.
Recurrencias lineales
Una sucesión recursiva es lineal si su relación de recurrencia expresa el término \(a_n\) como una combinación lineal de un número fijo de términos anteriores. Esto significa que no aparecen potencias (como \(a_{n-1}^2\)), productos entre términos anteriores (como \(a_{n-1} \cdot a_{n-2}\)) ni otras funciones complejas de ellos.
La forma general de una sucesión lineal de orden \(k\) es:
\(a_n=c_1 \cdot a_{n-1}+c_2 \cdot a_{n-2}+... +c_k \cdot a_{n-k}+g(n)\)
donde \(c_1, c_2,..., c_k\) son constantes y \(g(n)\) es una función que depende solo de \(n.\)
Dentro de las sucesiones lineales, se distingue entre homogéneas y no homogéneas. La sucesión es lineal homogénea si la función \(g(n)\) es cero para todo \(n,\) es decir, no existe un término independiente que dependa de \(n\) (por ejemplo, \(a_n=2a_{n-1}-a_{n-2}\) o la sucesión de Fibonacci \(F_n=F_{n-1}+F_{n-2}\)). Por el contrario, es lineal no homogénea cuando \(g(n) ≠ 0,\) añadiendo un término extra que puede ser una constante o una función de \(n\) (por ejemplo, \(a_n=a_{n-1}+2n\)).
Sucesiones recursivas no lineales
Una sucesión recursiva es no lineal si la relación de recurrencia involucra términos anteriores de una manera que no es una combinación lineal. Esto incluye la presencia de productos entre términos, potencias, funciones trigonométricas, u otras operaciones no lineales. Estas sucesiones suelen ser más complejas de analizar y resolver que las lineales.
Algunos ejemplos son:
- \(a_n=a_{n-1} \cdot a_{n-2}\) (producto de términos anteriores).
- \(a_n=(a_{n-1})^2+c\) (término anterior elevado al cuadrado).
- \(a_n=\dfrac{1}{2} \left(a_{n-1}+\dfrac{A}{a_{n-1}}\right),\) utilizada para aproximar la raíz cuadrada de A, conocida como método babilónico o de Herón.
Cómo encontrar una fórmula explícita
El principal inconveniente de una definición recursiva es su ineficacia para calcular términos muy avanzados. Por ejemplo, hallar el término a100 requiere calcular los 99 anteriores. Para solucionarlo, se busca una fórmula explícita o cerrada, que exprese an en función solo de n y de los valores iniciales, este proceso se conoce como resolver una sucesión recursiva.
Esto no solo agiliza los cálculos, sino que también facilita el análisis de propiedades como la convergencia de la sucesión. Existen varios métodos para encontrar esta fórmula, veremos dos a continuación.
Método de iteración o sustitución hacia atrás
Este es el método más sencillo y se aplica principalmente a sucesiones recurrentes de primer orden. La idea es aplicar repetidamente la relación de recurrencia, expresando \(a_n\) en términos de \(a_{n-1},\) luego \(a_{n-1}\) en términos de \(a_{n-2},\) y así sucesivamente hasta llegar al término inicial, con el objetivo de detectar un patrón.
Los pasos generales son:
- Escribir an en función de an-1 usando la relación de recurrencia.
- Sustituir la expresión de an-1 (que estará en función de an-2) en la ecuación del paso anterior.
- Repetir este proceso de sustitución "hacia atrás" hasta expresar an en función del término inicial a1.
- Simplificar la expresión resultante para obtener la fórmula explícita.
- Para más rigurosidad, probar la fórmula mediante inducción matemática.
Ejemplo 1
Aplicar el método de iteración para encontrar la fórmula general de una progresión aritmética.
Solución
Partimos de la definición recursiva general de una sucesión aritmética: un primer término \(a_1\) y la relación de recurrencia \(a_n=a_{n-1}+d\) para \(n ≥ 2.\) Aplicamos el método de iteración hacia atrás:
Comenzamos con la expresión para un término general \(a_n:\)
\(a_n=a_{n-1}+d\)
Sustituimos la expresión de \(a_{n-1},\) que es \(a_{n-1}=a_{n-2}+d:\)
\(a_n=(a_{n-2}+d)+d=a_{n-2}+2d\)
Sustituimos ahora \(a_{n-2}=a_{n-3}+d:\)
\(a_n=(a_{n-3}+d)+2d=a_{n-3}+3d\)
Continuamos este patrón. Tras la cuarta sustitución, tendríamos \(a_n=a_{n-4}+4d.\) Podemos observar que, después de \((n-1)\) sustituciones, el subíndice del término \(a\) se reduce hasta llegar a \(a_1,\) y el coeficiente de \(d\) se convierte en \((n-1).\) Esto nos lleva a la fórmula general:
\(a_n=a_1+(n-1)d\)
Por lo tanto, la fórmula explícita para cualquier sucesión aritmética es \(a_n=a_1+(n-1)d.\)
Para ilustrar con un caso particular, si tenemos \(a_1=3\) y \(d=5,\) la fórmula se convierte en \(a_n=3+(n-1)\cdot5=5n-2.\) Esto nos permite calcular, por ejemplo, \(a_{100}=5\cdot100-2=498\) de forma inmediata.
Ejemplo 2
Utilizar la iteración para hallar la fórmula cerrada de una sucesión geométrica.
Solución
Consideremos la definición recursiva general de una sucesión geométrica: un primer término \(a_1\) y la relación \(a_n=r \cdot a_{n-1}\) para \(n ≥ 2.\) Procedemos a iterar hacia atrás:
Empezamos con la relación fundamental:
\(a_n=r \cdot a_{n-1}\)
Sustituimos \(a_{n-1}\) por su expresión equivalente, \(a_{n-1}=r \cdot a_{n-2}:\)
\(a_n=r \cdot (r \cdot a_{n-2})=r^2 \cdot a_{n-2}\)
Sustituimos \(a_{n-2}=r \cdot a_{n-3}:\)
\(a_n=r^2 \cdot (r \cdot a_{n-3})=r^3 \cdot a_{n-3}\)
En una cuarta iteración, obtendríamos \(a_n=r^4 \cdot a_{n-4}.\) El patrón es claro: cada sustitución incrementa el exponente de la razón \(r\) en una unidad y disminuye el subíndice de \(a\) en una unidad. Después de \((n-1)\) iteraciones, llegamos al término inicial:
\(a_n=r^{n-1} \cdot a_1\)
Entonces, la fórmula explícita universal para una sucesión geométrica es: \(a_n=a_1 \cdot r^{n-1}.\)
Aplicando esta fórmula a un caso concreto, si \(a_1=2\) y \(r=3,\) la fórmula es \(a_n=2 \cdot 3^{n-1}.\) Así, podemos hallar directamente el décimo término: \(a_{10}=2 \cdot 3^{9}=39366.\)
Ejemplo 3
Obtener la fórmula explícita del factorial mediante el método de sustitución hacia atrás.
Solución
Partimos de la definición recursiva del factorial: \(a_1=1\) y la relación de recurrencia \(a_n=n \cdot a_{n-1}\) para \(n ≥ 2.\) Aplicamos el proceso de sustitución hacia atrás para expresar \(a_n\) en términos del valor inicial.
Comenzamos con la relación para un término general:
\(a_n=n \cdot a_{n-1}\)
Sustituimos la expresión de \(a_{n-1},\) que es \(a_{n-1}=(n-1) \cdot a_{n-2}:\)
\(a_n=n \cdot [(n-1) \cdot a_{n-2}]=n(n-1) \cdot a_{n-2}\)
Sustituimos ahora \(a_{n-2}=(n-2) \cdot a_{n-3}:\)
\(a_n=n(n-1) \cdot [(n-2) \cdot a_{n-3}]=n(n-1)(n-2) \cdot a_{n-3}\)
Continuando con una cuarta sustitución, \(a_{n-3}=(n-3) \cdot a_{n-4},\) obtenemos:
\(a_n=n(n-1)(n-2)(n-3) \cdot a_{n-4}\)
Al observar el patrón, vemos que con cada iteración se incorpora un factor entero decreciente al producto. Después de \((n-1)\) sustituciones, el subíndice de \(a\) se reduce a 1, y habremos multiplicado por todos los números enteros desde \(n\) hasta \(2.\) Esto nos conduce a la fórmula explícita:
\(a_n=n(n-1)(n-2) \cdots (3) \cdot (2) \cdot a_1\)
Dado que \(a_1=1,\) la fórmula final para el término general, que reconocemos como el factorial de \(n,\) es:
\(a_n=n!=n \cdot (n-1) \cdot (n-2) \cdots 3 \cdot 2 \cdot 1\)
Por ejemplo, para calcular \(5!\) usando esta fórmula, simplemente realizamos el producto: \(5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120.\)
Es importante entender que el método de iteración nos permite conjeturar una fórmula explícita a partir de un patrón observado. Sin embargo, para demostrar de manera formal y rigurosa que esta fórmula es válida para todo número natural n, es necesario utilizar el principio de inducción matemática.
La inducción es un método de demostración que consta de dos pasos esenciales. Primero, se verifica que la fórmula es cierta para el caso inicial, normalmente n = 1. Segundo, se supone que la fórmula es válida para un valor arbitrario n = k (esta suposición se llama hipótesis de inducción) y, utilizando esta suposición, se demuestra que la fórmula también se cumple para el siguiente valor, n = k + 1. Al completar estos pasos, se prueba que la fórmula es correcta para todos los números naturales n.
Método de la ecuación característica
Este método es una potente herramienta para encontrar una fórmula explícita de sucesiones definidas por relaciones de recurrencia lineales, homogéneas y con coeficientes constantes. Estas relaciones tienen la forma general:
\(a_n=c_1 a_{n-1}+c_2 a_{n-2}+\dots+c_k a_{n-k}\)
donde \(c_1, c_2, \dots, c_k\) son constantes. Para simplificar la explicación, nos centraremos en el caso de segundo orden (\(k=2\)), cuya forma es:
\(a_n=c_1 a_{n-1}+c_2 a_{n-2}\)
El procedimiento se basa en suponer que la fórmula general es una potencia, es decir, \(a_n=r^n,\) donde \(r\) es un número (real o complejo) a determinar. Si sustituimos esta solución tentativa en la relación de recurrencia, obtenemos:
\(r^n=c_1 r^{n-1}+c_2 r^{n-2}\)
Podemos simplificar esta ecuación dividiendo ambos lados por \(r^{n-2}\) (asumiendo \(r ≠ 0\)), lo que nos lleva a la ecuación característica:
\(r^2-c_1 r-c_2=0\)
La naturaleza de las raíces de esta ecuación cuadrática determina la forma de la solución general.
1) Raíces reales y distintas (\(r_1 ≠ r_2\)): la solución general es una combinación lineal de las potencias de ambas raíces:
\(a_n=A r_1^n+B r_2^n\)
donde las constantes A y B se determinan usando los valores iniciales de la sucesión.
2) Raíz real doble (\(r_1=r_2\)): cuando la ecuación característica tiene una única solución \(r,\) la solución general incorpora un factor lineal en \(n:\)
\(a_n=A r^n+B n r^n\)
Nuevamente, A y B se calculan a partir de los términos iniciales.
3) Raíces complejas conjugadas: Si las raíces son de la forma \(r_{1,2}=p±qi,\) es útil expresarlas en forma polar. Sean \(\rho=\sqrt{p^2+q^2}\) el módulo y \(\theta=\arctan(q/p)\) el argumento. La solución general se escribe como:
\(a_n=\rho^n (A \cos(n\theta)+B \sin(n\theta))\)
donde las constantes A y B se determinan usando los valores iniciales.
El proceso completo consiste, por tanto, en:
- Plantear la ecuación característica.
- Encontrar las raíces.
- Escribir la solución general según el tipo de raíces.
- Calcular las constantes usando los valores iniciales para obtener la solución particular.
Ejemplo
Encontrar una fórmula general para la sucesión de Fibonacci.
Solución
Partimos de la definición de la sucesión de Fibonacci: \(F_1=1\), \(F_2=1\) y \(F_n=F_{n-1}+F_{n-2}\) para \(n ≥ 3.\) Esta es una relación de recurrencia lineal, homogénea y de segundo orden. Para aplicar el método, suponemos una solución de la forma \(F_n=r^n.\)
Sustituyendo en la recurrencia \(F_n-F_{n-1}-F_{n-2}=0,\) obtenemos:
\(r^n-r^{n-1}-r^{n-2}=0\)
Dividimos toda la ecuación por \(r^{n-2}\) (válido para \(r ≠ 0\)) para llegar a la ecuación característica:
\(r^2-r-1=0\)
Resolvemos esta ecuación cuadrática, cuyas soluciones son:
\(r_1=\dfrac{1+\sqrt{5}}{2}=\varphi, \quad r_2=\dfrac{1-\sqrt{5}}{2}=\psi\)
Estas son las famosas proporción áurea \(\varphi\) y su conjugado \(\psi.\) Como son raíces reales y distintas, la solución general es una combinación lineal:
\(F_n=A \varphi^n+B \psi^n\)
Ahora determinamos las constantes \(A\) y \(B\) usando las condiciones iniciales. Para \(n=1:\)
\(F_1=A \varphi+B \psi=1\)
Para \(n=2:\)
\(F_2=A \varphi^2+B \psi^2=1\)
Resolviendo este sistema de ecuaciones y aprovechando las propiedades \(\varphi^2=\varphi+1\) y \(\psi^2=\psi+1,\) encontramos que:
\(A=\dfrac{1}{\sqrt{5}}, \quad B=-\dfrac{1}{\sqrt{5}}\)
Sustituyendo estos valores en la solución general, llegamos a la fórmula de Binet:
\(F_n=\dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1+\sqrt{5}}{2} \right)^n-\left(\dfrac{1-\sqrt{5}}{2} \right)^n \right]\)
Esta fórmula es notable por varias razones. Primero, nos permite calcular cualquier término de Fibonacci directamente, sin necesidad de calcular todos los anteriores. Por ejemplo, para hallar \(F_{10}:\)
\(F_{10}=\dfrac{1}{\sqrt{5}} \left[ \varphi^{10}-\psi^{10} \right]=55\)
Segundo, a pesar de que la fórmula contiene números irracionales (\(\sqrt{5}\)), las potencias y la resta se combinan de tal manera que el resultado final es siempre un número entero para cualquier valor natural de n.
Convergencia de sucesiones recursivas
Podemos estudiar la convergencia de una sucesión recurrente incluso sin tener una fórmula explícita para el término general. Un teorema fundamental establece que toda sucesión monótona (creciente o decreciente) y acotada es convergente. Por lo tanto, la estrategia para demostrar la convergencia suele seguir estos pasos:
- Acotación: probar que la sucesión está acotada superiormente o inferiormente.
- Monotonía: demostrar que la sucesión es siempre creciente o siempre decreciente.
- Conclusión de convergencia: una vez verificadas la acotación y la monotonía, podemos afirmar que la sucesión converge a un límite L.
- Cálculo del límite: suponiendo que \(\lim_{n \to ∞} a_n=L,\) sustituimos este límite en la relación de recurrencia. Dado que para n grande, \(a_n\) y \(a_{n-1}\) se aproximan a L, podemos plantear una ecuación en L y resolverla para encontrar su valor.
Ejemplo
Analizar la convergencia de la sucesión definida por la fórmula babilónica para aproximar \(\sqrt{3}.\)
Solución
Consideremos la sucesión definida para \(A=3\) con un valor inicial \(a_1=2:\)
\(a_n=\dfrac{1}{2} \left(a_{n-1}+\dfrac{3}{a_{n-1}} \right) \text{ para } n ≥ 2\)
Primero demostramos que la sucesión está acotada inferiormente. Para cualquier término positivo \(a_{n-1}>0,\) podemos comparar las expresiones \(a_{n-1}\) y \(3/a_{n-1}.\) Notamos que su media aritmética siempre es mayor o igual que su media geométrica:
\(\dfrac{a_{n-1}+\dfrac{3}{a_{n-1}}}{2} ≥ \sqrt{a_{n-1} \cdot \dfrac{3}{a_{n-1}}}=\sqrt{3}\)
Como \(a_n\) es precisamente esta media aritmética, tenemos que \(a_n ≥ \sqrt{3}\) para todo \(n ≥ 2.\) Dado que \(a_1=2>\sqrt{3},\) la sucesión está acotada inferiormente por \(\sqrt{3}.\)
Ahora estudiamos la monotonía. Calculamos la diferencia:
\(a_n-a_{n-1}=\dfrac{1}{2} \left(a_{n-1}+\dfrac{3}{a_{n-1}} \right)-a_{n-1}=\dfrac{3-a_{n-1}^2}{2a_{n-1}}\)
Dado que \(a_{n-1} ≥ \sqrt{3}\) para \(n ≥ 2,\) entonces \(a_{n-1}^2 ≥ 3,\) por lo que el numerador \(3-a_{n-1}^2 ≤ 0.\) Como el denominador \(2a_{n-1}>0,\) tenemos \(a_n-a_{n-1} ≤ 0 → a_n ≤a_{n-1}.\) Esto prueba que la sucesión es decreciente para \(n ≥ 2.\)
Al ser decreciente y estar acotada inferiormente, concluimos que la sucesión converge. Sea L su límite. Para calcular L, tomamos el límite de la relación de recurrencia:
\(\lim_{n \to ∞} a_n=\lim_{n \to ∞} \dfrac{1}{2} \left(a_{n-1}+\dfrac{3}{a_{n-1}} \right)\)
Lo cual implica que:
\(L=\dfrac{1}{2} \left(L+\dfrac{3}{L} \right)\)
Multiplicamos ambos lados por \(2L\) (suponiendo \(L ≠ 0,\) lo cual es cierto porque \(L ≥ \sqrt{3}>0\)):
\(2L^2=L^2+3\)
Simplificando, obtenemos \(L^2=3.\) Dado que sabemos que \(L>0,\) la única solución posible es \(L=\sqrt{3}.\) Así, hemos demostrado que la sucesión converge efectivamente a la raíz cuadrada de 3.
Bibliografía
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

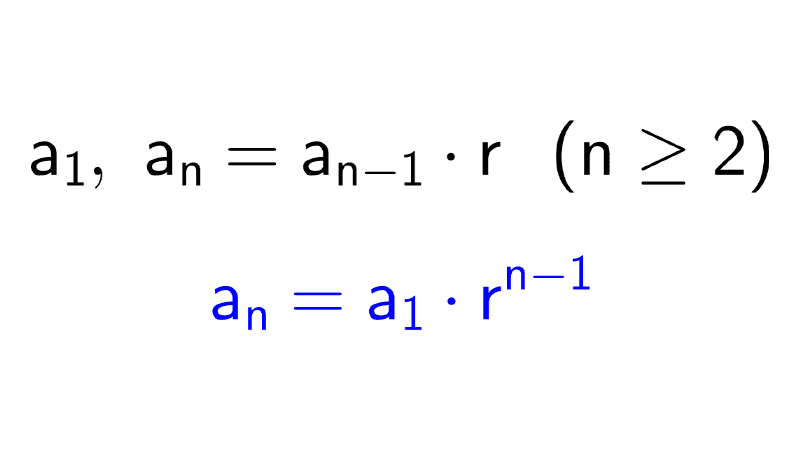
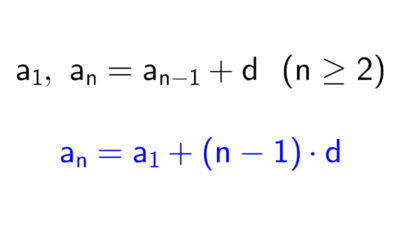
Otros artículos que pueden interesarte