Sucesión oscilante

Una sucesión oscilante es un tipo de sucesión divergente que no posee límite finito ni infinito. Su característica principal es que sus términos fluctúan sin estabilizarse en ningún valor específico, ni se alejan indefinidamente hacia el infinito o menos infinito, por ese motivo la secuencia recibe el nombre de “oscilante”.

Existen dos formas de oscilación: la oscilación finita (o periódica), donde los términos alternan entre un conjunto finito de valores, y la oscilación infinita, cuando los términos van creciendo en valor absoluto pero alternando su signo.

Ejemplos

Algunos ejemplos de sucesiones oscilantes son:  

• ( (-1)ⁿ ) = (-1, 1, -1, 1, -1, …), los valores de esta sucesión saltan entre -1 y 1, diverge por oscilación finita.  
• (0, 1, 2, 0, 1, 2, …), en esta sucesión los términos alternan entre tres valores que se repiten constantemente: 0, 1 y 2.  
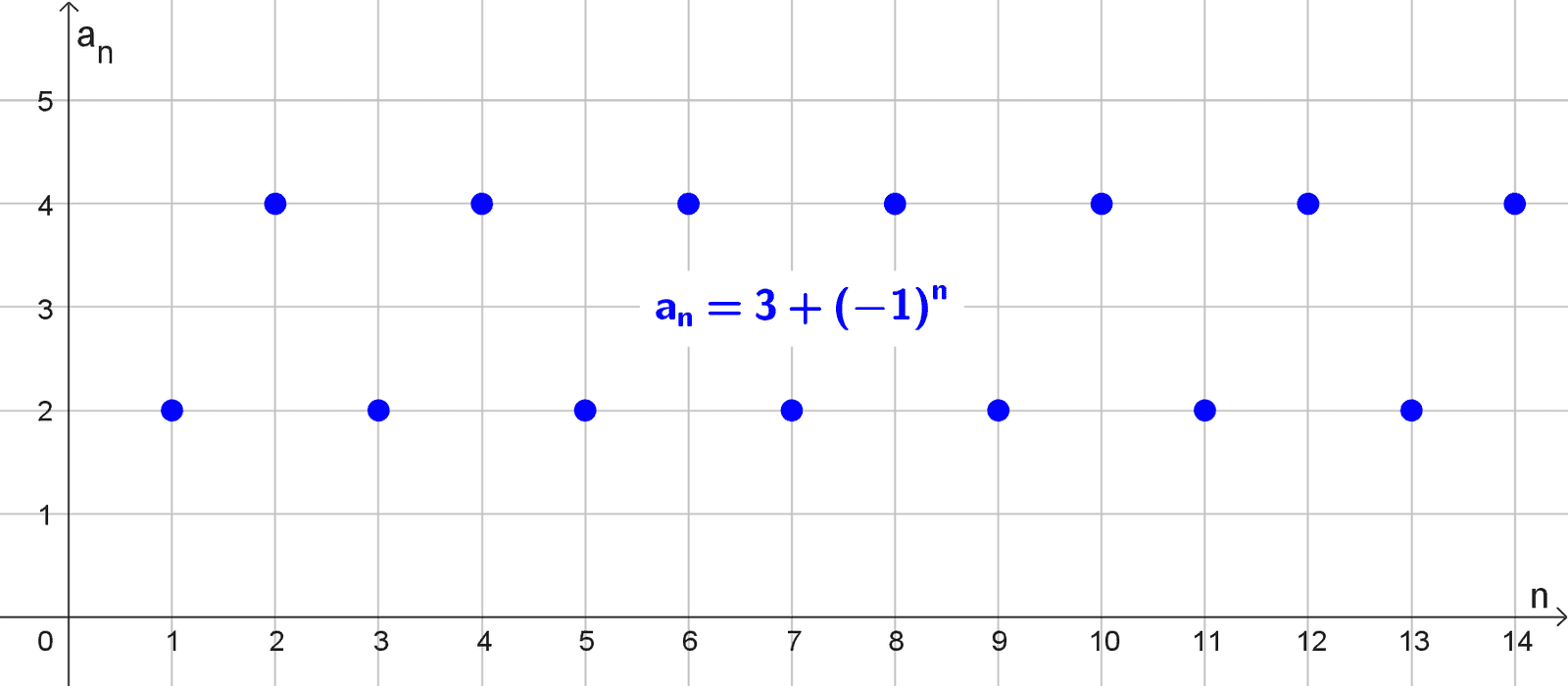
• ( 3 + (-1)ⁿ ) = (4, 2, 4, 2, 4, 2, …), es una sucesión oscilante entre los valores 4 y 2.  
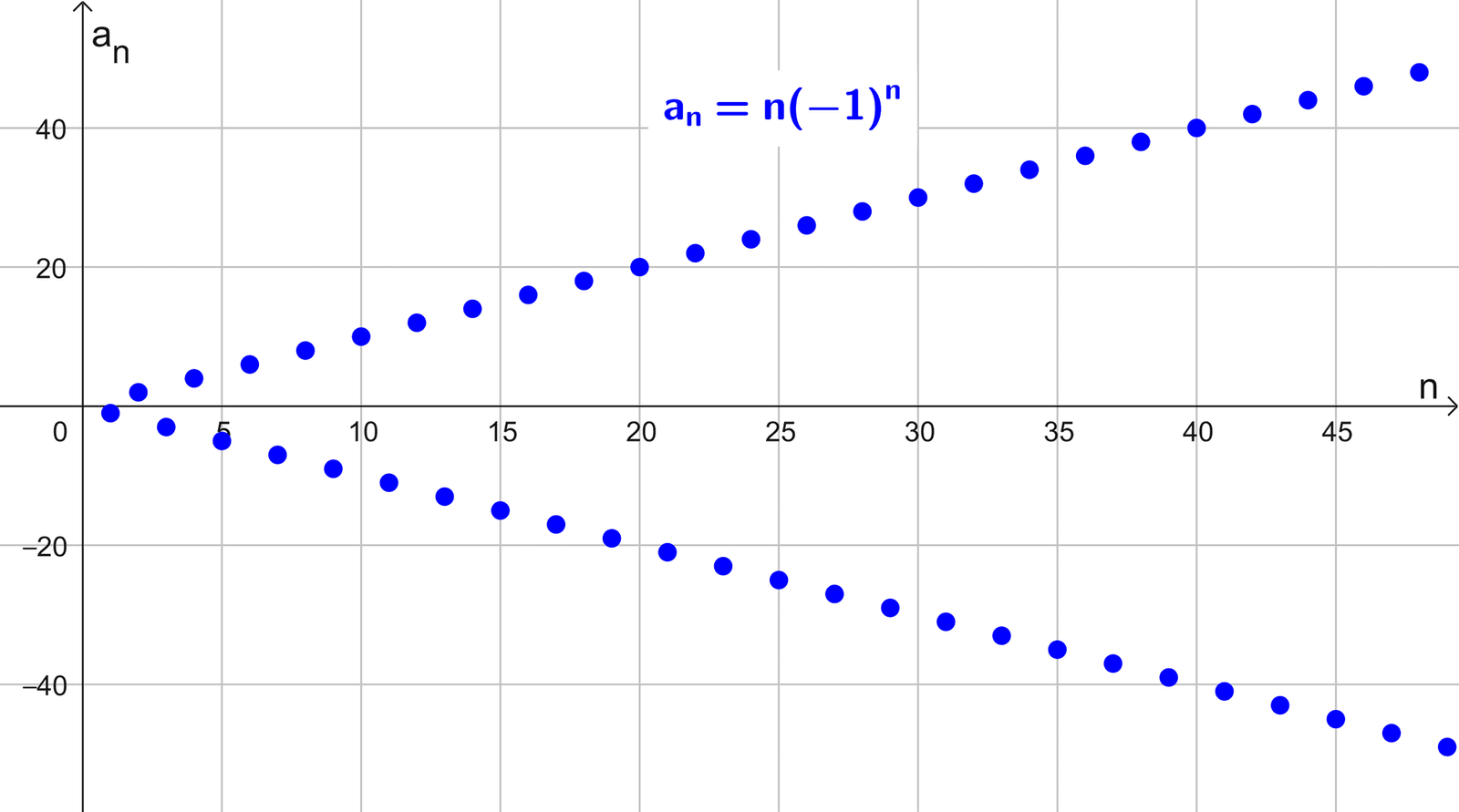
• ( n(-1)ⁿ ) = (-1, 2, -3, 4, -5, 6, -7, …), los términos crecen en valor absoluto pero alternan de signo en cada paso, por lo que no diverge a infinito ni menos infinito, sino que diverge por oscilación infinita.  
• La sucesión definida por a_n = (-1)ⁿ (1 + 1/n) es oscilante.
• Los términos de las sucesiones definidas por sin(n) y cos(n) (seno y coseno) oscilan continuamente en el intervalo [-1, 1] sin repetir un patrón periódico.  

Es fundamental no confundir sucesión oscilante con sucesión alternada. Una sucesión alternada es aquella en la que cada término tiene signo contrario al anterior, es decir, cambia de positivo a negativo de manera sistemática. Pero esto no implica necesariamente divergencia: por ejemplo, ( (-1)ⁿ / n ) = (-1, 1/2, -1/3, 1/4, -1/5, …) es alternada y converge a cero. 

En cambio, una sucesión oscilante, por definición, no converge jamás. Además, mientras que toda sucesión alternada cambia de signo, una oscilante puede hacerlo o no: el ejemplo (0, 1, 2, 0, 1, 2, …) no alterna signos, pues todos sus términos son no negativos, mientras que en (-1, 1, -1, 1, -1, …) los términos sí alternan signos.

Características

• Inexistencia de límite: la característica fundamental es que una sucesión oscilante carece de límite. Esto significa que no se aproxima de manera definitiva a un único valor finito, ni diverge hacia infinito o menos infinito. Su comportamiento permanece indefinido a medida que avanzamos en sus términos.
• Comportamiento no monótono: por definición, una sucesión oscilante no puede ser monótona. Esto descarta que sea exclusivamente creciente, exclusivamente decreciente o constante.
• Comportamiento impredecible: los términos de la sucesión "saltan" o "alternan" entre diferentes valores o rangos de valores, sin seguir un patrón que establezca una tendencia clara y única a largo plazo.
• Pueden ser acotadas o no acotadas: una sucesión oscilante puede ser acotada, es decir, todos sus términos se encuentran confinados entre dos valores reales fijos. Por el contrario, también puede ser no acotada, donde los términos crecen en valor absoluto de manera ilimitada.

Cómo identificar una sucesión oscilante

A continuación, detallamos los pasos a seguir para identificar una sucesión oscilante.

1) Analizar el comportamiento de los primeros términos

Comenzamos calculando los primeros cinco o seis términos de la sucesión. Nos fijamos si hay un patrón repetitivo en los signos (por ejemplo, positivo, negativo, positivo) o si los valores suben y bajan sin acercarse a un número concreto. Este análisis inicial nos dará una intuición numérica del comportamiento. Podemos complementar esta observación con una representación gráfica.

2) Calcular el límite de la sucesión

Intentamos calcular el límite *\lim_{n \to ∞} a_n.* Si este límite no existe (es decir, la sucesión no se acerca a ningún valor real, ni tampoco diverge a *+∞* o *-∞*) o no se puede calcular de la forma habitual (por ejemplo, si aparece un factor (-1)ⁿ), entonces tenemos un fuerte indicio de que la sucesión es oscilante.

3) Estudiar el comportamiento de subsucesiones

Una técnica para demostrar la no existencia del límite es analizar subsucesiones. Si encontramos dos subsucesiones que tienen límites diferentes, habremos probado que el límite de la sucesión principal no existe. Esto se debe a que, si una sucesión tiene límite (finito o infinito), todas sus subsucesiones deben tener el mismo límite.

Las subsucesiones más comunes para este fin son la de los términos de índice par (*a_{2k}*) y la de los términos de índice impar (*a_{2k-1}*). Calculamos el límite de cada una por separado y, si estos límites son distintos, la sucesión original es oscilante. 

Ejemplo

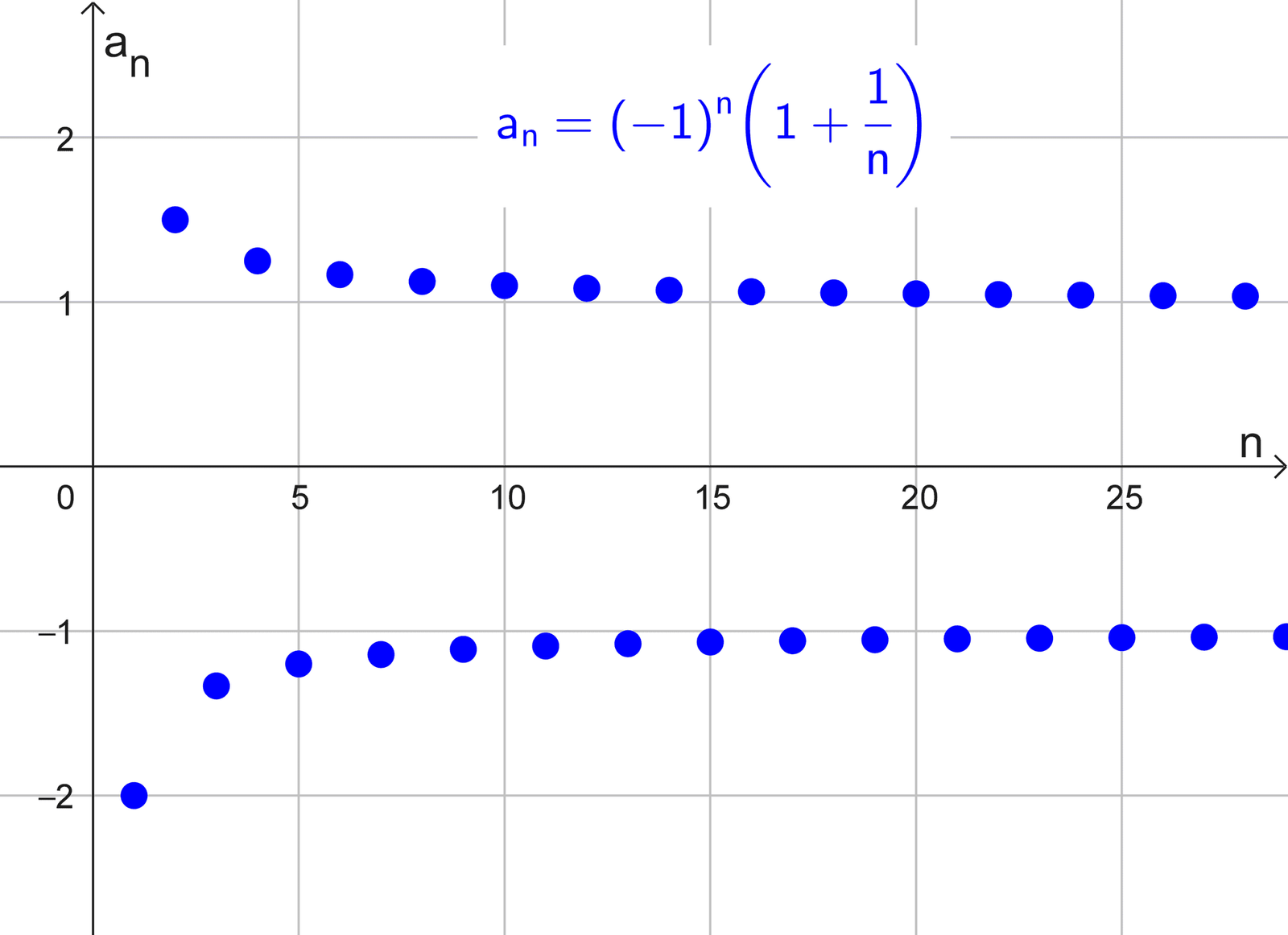
Analizar si la sucesión definida por *a_n=(-1)^n \left(1+\dfrac{1}{n}\right)* es oscilante.

Solución

Comenzamos calculando los primeros términos para *n=1, 2, 3, 4, 5:*

*a_1=(-1)^1 (1+1)=-2*

*a_2=(-1)^2 (1+1/2)=1,5*

*a_3=(-1)^3 (1+1/3) ≈-1,33*

*a_4=(-1)^4 (1+1/4)=1,25*

*a_5=(-1)^5 (1+1/5)=-1,2*

*a_6=(-1)^6 (1+1/6)≈1,17*

Observamos que los signos alternan y los valores absolutos decrecen, acercándose a -1 y 1 respectivamente. En la gráfica podemos ver este mismo comportamiento:

Intentamos calcular el límite de la sucesión: 

*\lim_{n \to ∞} (-1)^n \left(1+\dfrac{1}{n}\right)*

Aquí ocurre que *\left(1+\dfrac{1}{n}\right) \to 1,* pero el factor *(-1)^n* oscila entre -1 y 1, impidiendo que el límite exista. No diverge a infinito, por lo que es candidata a oscilante.

Finalmente, analizamos las subsucesiones de pares e impares:

• Límite de los pares: *\lim_{k \to ∞} a_{2k}=\lim_{k \to ∞} (1)\left(1+\dfrac{1}{2k}\right)=1*
• Límite de los impares: *\lim_{k \to ∞} a_{2k-1}=\lim_{k \to ∞} (-1)\left(1+\dfrac{1}{2k-1}\right)=-1*

Como los límites de las subsucesiones son diferentes (1 y -1), concluimos formalmente que la sucesión definida por el término general *a_n=(-1)^n \left(1+\dfrac{1}{n}\right)* es oscilante.

Bibliografía

• Apostol, T. (1984). Calculus: Cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
• Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
• Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación. 
• Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15.ª ed.). El Ateneo. 
• Stewart, J. (2012). Cálculo de una variable: Trascendentes tempranas (7.ª ed.). Cengage Learning. 
• Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: Matemáticas para el cálculo (6.ª ed.). Cengage Learning. 
• Zill, D. y Wright, W. (2011). Cálculo: Trascendentes tempranas (4.ª ed.). McGraw-Hill Education.