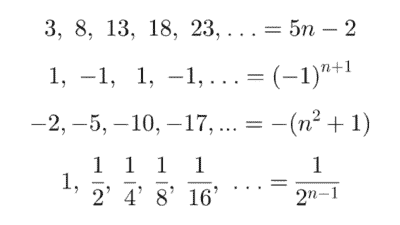
Sucesiones numéricas
Una sucesión es un conjunto ordenado de números, llamados términos, dispuestos según una regla que determina su posición en la secuencia. Cada término ocupa un lugar específico, indicado por un número natural. Las sucesiones pueden ser finitas, si tienen un número limitado de términos, o infinitas, si continúan indefinidamente.
Por ejemplo:
- La secuencia 2, 4, 6, 8, 10 es una sucesión finita: tiene un número limitado de términos y un último elemento claramente definido. El primer término es 2 y el último es 10.
- La sucesión de números impares 1, 3, 5, 7, 9, 11, … es una sucesión infinita, ya que no tiene un término final. Usamos los puntos suspensivos (...) para indicar que continúa indefinidamente.
- La secuencia de fracciones 1, 1/2, 1/3, 1/4, 1/5, … es otra sucesión infinita.
En el lenguaje cotidiano, las palabras «sucesión» y «serie» suelen usarse como sinónimos, pero en Matemática tienen significados distintos. Una sucesión es un conjunto ordenado de números, donde cada elemento ocupa una posición específica. En cambio, una serie es la suma de los términos de una sucesión. En este artículo nos enfocaremos exclusivamente en el estudio de las sucesiones numéricas infinitas.
Índice
Definición matemática
Debido a que una sucesión es una lista ordenada y cada elemento puede ser asociado con un número natural (1, 2, 3, 4, …), podemos definir a una sucesión como una función entre el conjunto de los números naturales (enteros positivos) y el conjunto de los números reales. Es decir, cada número natural se asocia con un número real, que representa el valor del término correspondiente en la sucesión.
Formalmente, una sucesión es una función a cuyo dominio es el conjunto de los números naturales y cuyo codominio es el conjunto de los números reales. Simbólicamente:
\(a: \mathbb{N}~ \to ~ \mathbb{R}~ /~ ∀n \in \mathbb{N}: a(n)=a_n\)
En lugar de simbolizar a los términos de la sucesión con la notación habitual de funciones como a(1), a(2), a(3), …, a(n), … utilizaremos una forma más compacta con subíndices: a1, a2, a3, …, an, … donde el subíndice indica la posición del término en la secuencia. El elemento an se denomina n-ésimo término de la sucesión. Además, en lugar de usar las letras tradicionales para funciones como f, g, h, es habitual emplear las letras a, b, c, etc. para las distintas sucesiones. La letra n se llama índice de an y es habitual también usar la letra k.
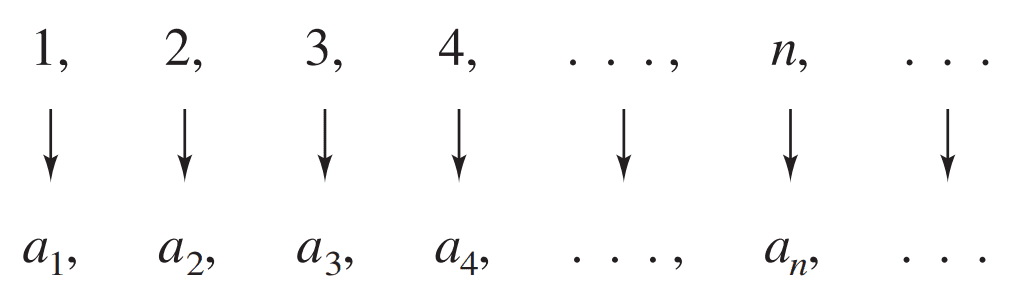
Las sucesiones se escriben utilizando paréntesis o llaves: (an) o {an}, también son válidas las formas \((a_n)_{n=1}^{\infty}\) y \(\{a_n\}_{n=1}^{\infty}.\) Por ejemplo:
(an) = (a1, a2, a3, …, an, …)
(bn) = (b1, b2, b3, …, bn, …)
Es importante tener cuidado, porque an es el enésimo término de la sucesión, mientras que (an) denota a la sucesión completa.
Ejemplos
Los ejemplos más comunes de sucesiones se pueden construir dando una regla o fórmula que defina el término n-ésimo. Esta se conoce como una fórmula general.
- La fórmula \(a_n=\dfrac{1}{n}\) define a la sucesión \((a_n)=\left(1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, …\right).\)
- La regla \(b_n=5n\) forma la secuencia \((b_n)=(5, 10, 15, 20, 25, 30, …).\)
- La fórmula \(c_n=2n-1\) define la sucesión de números impares \((c_n)=(1, 3, 5, 7, 9, 11, …).\)
- La fórmula \(d_n=n\) define la sucesión de números naturales \((d_n)=(1, 2, 3, 4, 5, 6, …).\)
Si una sucesión está dada por una fórmula general, para conocer el término que ocupa la posición n, basta con sustituir su valor en la fórmula, del mismo modo que hacemos con las funciones de variable real.
Por ejemplo, con la fórmula \(a_n=2n+1\) podemos encontrar todos los términos de la sucesión:
\(a_{\color{red}1}=2\cdot {\color{red}1}+1=3\)
\(a_{\color{red}2}=2\cdot {\color{red}2}+1=5\)
\(a_{\color{red}3}=2\cdot {\color{red}3}+1=7\)
\(a_{\color{red}4}=2\cdot {\color{red}4}+1=9\)
Para hallar el término que ocupa el lugar 157 de esta sucesión, usamos n = 157 en la fórmula:
\(a_{\color{red}157}=2\cdot {\color{red}157}+1=314+1=315\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
4,8 / 5 — 6 votos
Una sucesión también puede estar definida por distintas reglas, dependiendo del valor de n, por ejemplo:
\(a_n=\begin{cases}n,~\text{si n es par} \\ -n, ~\text{si n es impar} \end{cases}\)
La sucesión es:
(-1, 2, -3, 4, -5, 6, …)
Ahora bien, no todas las sucesiones tienen fórmula general, por ejemplo, la sucesión de números primos:
(2, 3, 5, 7, 11, 13, 17, 19, 23, …)
Hasta ahora no se ha encontrado una fórmula que permita obtener en n-ésimo número primo.
Una lista como (..., -3, -2, -1, 0, 1, 2, 3, …) no es una sucesión porque no tiene primer elemento, sino que se extiende infinitamente en ambos sentidos. En cambio, (0, 1, -1, 2, -2, 3, -3, …) sí es una sucesión. Nótese que el conjunto de valores de esta sucesión es el conjunto Z de los números enteros.
Otra forma de determinar una sucesión es por recurrencia o recursividad, que consiste en definir el primer término (o algunos iniciales) y una regla que permita obtener los siguientes a partir de uno o varios anteriores. Por ejemplo:
\(a_1=1, a_{n}=a_{n-1}+2~ \text{para n > 1}\)
La expresión anterior dice: "el primer término es 1, el enésimo término es igual al término anterior (n-1) más dos". Aplicando la regla:
\(a_1=1\)
\(a_2=a_1+2=1+2=3\)
\(a_3=a_2+2=3+2=5\)
\(a_4=a_3+2=5+2=7\)
Es decir, la sucesión es: (1, 3, 5, 7, …). Para obtener el n-ésimo término ya no se puede sustituir directamente en la fórmula, sino que hace falta conocer los términos anteriores.
Un caso conocido es la sucesión de Fibonacci, donde los primeros dos términos son iguales a 1 y los siguientes se obtienen sumando los dos anteriores:
\(F_1=1,~ F_2=1,~ F_n=F_{n-1}+F_{n-2}~ \text{para n > 2}\)
Escribimos los primeros términos:
\(F_1=1\)
\(F_2=1\)
\(F_3=F_2+F_1=1+1=2\)
\(F_4=F_3+F_2=2+1=3\)
\(F_5=F_4+F_3=3+2=5\)
\(F_6=F_5+F_4=5+3=8\)
\(F_7=F_6+F_5=8+5=13\)
La sucesión de Fibonacci es:
(1, 1, 2, 3, 5, 8, 13, …)
Esta sucesión surgió cuando un matemático italiano del siglo XIII, conocido como Fibonacci, resolvió un problema relacionado con la cría de conejos.
Una misma sucesión puede definirse de formas diferentes, por ejemplo, la sucesión (5, 10, 15, 20, 25, 30, …) puede definirse por el término general \(a_n=5n,\) pero también podría pensarse como "comenzamos en 5 y sumamos 5 al término anterior cada vez", de este modo obtenemos la definición por recurrencia:
\(a_1=5,~ a_n=a_{n-1}+5\)
Ejercicio 1
Obtener los primeros seis términos de cada sucesión.
- \((a_n)=(3+(-1)^n)\)
- \((b_n)=n^2-1\)
- \((c_n)=\left(\dfrac{n}{1-2n}\right)\)
- \((d_n)=\left(\dfrac{n^2}{2^n-1}\right)\)
- \((e_n)\) donde \(d_1=25\) y \(d_n=d_{n-1}-5\)
- \(t_1=1\) y \(t_n=3(t_{n-1}+2)\)
Solución 1
Queremos obtener los primeros seis términos de la sucesión definida por:
\(a_n=3+(-1)^n\)
Esta es una sucesión explícita, es decir, el valor de cada término depende directamente del número n. El término \((-1)^n\) alterna entre 1 y -1, dependiendo de si n es par o impar. Por lo tanto, los valores de \(a_n\) para los primeros seis términos son:
\(a_1=3+(-1)^1=3-1=2\)
\(a_2=3+(-1)^2=3+1=4\)
\(a_3=3+(-1)^3=3-1=2\)
\(a_4=3+(-1)^4=3+1=4\)
\(a_5=3+(-1)^5=3-1=2\)
\(a_6=3+(-1)^6=3+1=4\)
Entonces, la sucesión es:
(2, 4, 2, 4, 2, 4, …)
Solución 2
La sucesión está definida por: \(b_n=n^2-1\)
Evaluamos para n = 1 hasta n = 6:
\(b_1=1^2-1=1-1=0\)
\(b_2=2^2-1=4-1=3\)
\(b_3=3^2-1=9-1=8\)
\(b_4=4^2-1=16-1=15\)
\(b_5=5^2-1=25-1=24\)
\(b_6=6^2-1=36-1=35\)
Entonces, la sucesión es:
(0, 3, 8, 15, 24, 35, …)
Solución 3
Calculamos los primeros seis términos de la sucesión dada por:
\(c_n=\dfrac{n}{1-2n}\)
Sustituimos n desde 1 hasta 6:
\(c_1=\dfrac{1}{1-2 \cdot 1}=\dfrac{1}{-1}=-1\)
\(c_2=\dfrac{2}{1-4}=\dfrac{2}{-3} ≈-0,67\)
\(c_3=\dfrac{3}{1-6}=\dfrac{3}{-5}=-0,6\)
\(c_4=\dfrac{4}{1-8}=\dfrac{4}{-7} ≈-0,57\)
\(c_5=\dfrac{5}{1-10}=\dfrac{5}{-9} ≈-0,56\)
\(c_6=\dfrac{6}{1-12}=\dfrac{6}{-11} ≈-0,55\)
La sucesión es:
\(\left(-1, -\dfrac{2}{3}, -\dfrac{3}{5}, -\dfrac{4}{7}, -\dfrac{5}{9}, -\dfrac{6}{11}, … \right)\)
En notación decimal:
(-1; -0,67; -0,6; -0,57; -0,56; -0,55; …)
Solución 4
Hallamos los primeros seis términos de la sucesión:
\(d_n=\dfrac{n^2}{2^n-1}\)
Evaluamos para n = 1 hasta n = 6:
\(d_1=\dfrac{1^2}{2^1-1}=\dfrac{1}{1}=1\)
\(d_2=\dfrac{4}{4-1}=\dfrac{4}{3} ≈ 1,33\)
\(d_3=\dfrac{9}{8-1}=\dfrac{9}{7} ≈ 1,28\)
\(d_4=\dfrac{16}{16-1}=\dfrac{16}{15} ≈ 1,07\)
\(d_5=\dfrac{25}{32-1}=\dfrac{25}{31} ≈ 0,81\)
\(d_6=\dfrac{36}{64-1}=\dfrac{36}{63} ≈ 0,57\)
La sucesión es:
\(\left(1, \dfrac{4}{3}, \dfrac{9}{7}, \dfrac{16}{15}, \dfrac{25}{31}, \dfrac{36}{63}, … \right)\)
En notación decimal:
(1; 1,33; 1,28; 1,07; 0,81; 0,57; …)
Solución 5
Determinamos los primeros seis términos de la sucesión recursiva definida por:
\(d_1=25\) y \(d_n=d_{n-1}-5\)
Partiendo del primer término, calculamos los siguientes restando 5 cada vez:
\(d_1=25\)
\(d_2=d_1-5=25-5=20\)
\(d_3=d_2-5=20-5=15\)
\(d_4=d_3-5=15-5=10\)
\(d_5=d_4-5=10-5=5\)
\(d_6=d_5-5=5-5=0\)
La sucesión es:
(25, 20, 15, 10, 5, 0, …)
Solución 6
Obtenemos los primeros seis términos de la sucesión recursiva definida por:
\(t_1=1\) y \(t_n=3(t_{n-1}+2)\)
Calculamos cada término aplicando la fórmula recursiva:
\(t_1=1\)
\(t_2=3(t_1+2)=3(1+2)=9\)
\(t_3=3(t_2+2)=3(9+2)=33\)
\(t_4=3(t_3+2)=3(33+2)=105\)
\(t_5=3(t_4+2)=3(105+2)=321\)
\(t_6=3(t_5+2)=3(321+2)=969\)
La sucesión es:
(1, 9, 33, 105, 321, 969, …)
Un ejercicio común en Cálculo es, a partir de una sucesión dada en forma de lista, obtener una fórmula general. Esto se consigue identificando el patrón que siguen los términos en la secuencia.
Ejercicio 2
Encuentre una fórmula para el término general de cada sucesión.
- \((-2, 4, -8, 16, -32, …)\)
- \(\left(\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{6}, \dfrac{7}{8}, …\right)\)
- \(\left(0, \dfrac{1}{4}, \dfrac{2}{9}, \dfrac{3}{16}, …\right)\)
- \(\left(\dfrac{3}{5}, -\dfrac{4}{25}, \dfrac{5}{125}, -\dfrac{6}{625}, \dfrac{7}{3125}, …\right)\)
Solución 1
La sucesión dada es: (-2, 4, -8, 16, -32, …)
Observamos que los valores absolutos siguen la progresión 2, 4, 8, 16, 32, que corresponde a una secuencia de las potencias de 2: \(2^n.\)
Notamos también que el primer término es negativo, el segundo positivo, el tercero negativo, etc., por lo tanto hay un patrón de alternancia de signo: \((-1)^n\) o \((-1)^{n+1}\) según cómo se defina. Debido a que el primer término es negativo, \((-1)^n\) es el factor correcto.
El término general de la sucesión es:
\(a_n=(-1)^n \cdot 2^n\)
Verificamos con algunos valores:
Para \(n=1:\) \((-1)^1 \cdot 2^1=-2\)
Para \(n=2:\) \((-1)^2 \cdot 2^2=1 \cdot 4=4\)
Para \(n=3:\) \((-1)^3 \cdot 2^3=-8\)
Para \(n=4:\) \((-1)^4 \cdot 2^4=16\)
Como los términos coinciden, el término general obtenido es correcto.
Solución 2
La sucesión dada es \(\left(\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{6}, \dfrac{7}{8}, …\right).\)
Cada término tiene numerador impar creciente y denominador par creciente. Observamos los patrones:
Numerador: \(1, 3, 5, 7, …=2n-1\)
Denominador: \(2, 4, 6, 8, …=2n\)
Por tanto, el término general se obtiene como:
\(a_n=\dfrac{2n-1}{2n}\)
Verificamos:
Para \(n=1\): \(\dfrac{1}{2}\)
Para \(n=2\): \(\dfrac{3}{4}\)
Para \(n=3\): \(\dfrac{5}{6}\)
Todos coinciden. Por lo tanto, una fórmula del término general es:
\(a_n=\dfrac{2n-1}{2n}\)
Solución 3
La sucesión dada es \(\left(0, \dfrac{1}{4}, \dfrac{2}{9}, \dfrac{3}{16}, …\right).\)
En esta sucesión los numeradores crecen linealmente: \(0, 1, 2, 3, …=n-1.\)
Los denominadores son los cuadrados de los naturales: \(1, 4, 9, 16, …=n^2\)
Así, el término general se puede escribir como:
\(a_n=\dfrac{n-1}{n^2}\)
Comprobamos:
Para \(n=1\): \(\dfrac{0}{1}=0\)
Para \(n=2\): \(\dfrac{1}{4}\)
Para \(n=3\): \(\dfrac{2}{9}\)
Para \(n=4\): \(\dfrac{3}{16}\)
Coincide en todos los casos, por tanto:
\(a_n=\dfrac{n-1}{n^2}\)
Solución 4
La sucesión dada es: \(\left(\dfrac{3}{5}, -\dfrac{4}{25}, \dfrac{5}{125}, -\dfrac{6}{625}, \dfrac{7}{3125}, …\right).\)
Esta sucesión alterna signos y los valores absolutos siguen el patrón:
Numeradores: \(3, 4, 5, 6, 7, …=n+2\)
Denominadores: \(5, 25, 125, 625, 3125, …=5^n\)
El signo alterna empezando con positivo, lo que sugiere un factor: \((-1)^{n+1}\)
Entonces podemos formular el término general como:
\(a_n=(-1)^{n+1} \cdot \dfrac{n+2}{5^n}\)
Verificación:
Para \(n=1\): \((-1)^2 \cdot \dfrac{3}{5}=\dfrac{3}{5}\)
Para \(n=2\): \((-1)^3 \cdot \dfrac{4}{25}=-\dfrac{4}{25}\)
Para \(n=3\): \((-1)^4 \cdot \dfrac{5}{125}=\dfrac{5}{125}\)
Todos los términos coinciden, así que una fórmula general es:
\(a_n=(-1)^{n+1} \cdot \dfrac{n+2}{5^n}\)
Formas de determinar una sucesión
A partir de los ejemplos anteriores, resumimos a continuación las formas de definir una sucesión:
| Método | Descripción | Ejemplos |
|---|---|---|
| Lista de los primeros términos | Consiste en dar una lista de los primeros términos de la sucesión, asumiendo que el patrón que siguen es evidente. | (2, 4, 6, 8, 10, 12, …) (5, 10, 15, 20, 25, 30, …) |
| Definición por una fórmula general (forma explícita) | Consiste en dar una fórmula para el enésimo término de la sucesión. | an = 5n bn = 3n + 1 |
| Definición por partes | Consiste en dar ciertas reglas que permiten obtener los términos dependiendo del valor del índice. | an = n (si n es par) an = n + 1 (si n es impar) |
| Definición recursiva | Consiste en definir uno o varios términos iniciales y una regla que permite obtener los siguientes a partir de uno o varios de los anteriores. | a1 = 1 an = an-1 + 2 (para n > 1) Sucesión de Fibonacci: F1 = F2 = 1 Fn = Fn-1 + Fn-2 (para n > 2) |
| Definición verbal o descriptiva | Consiste en describir con palabras la regla de formación de la sucesión. | "Sucesión de los números primos". "Sucesión de las potencias de 2". |
Gráfica de una sucesión
Una sucesión es una función, por tanto puede representarse gráficamente en el plano cartesiano. Sin embargo, a diferencia de las funciones reales, cuya gráfica suele ser una curva continua, la gráfica de una sucesión está formada por puntos aislados, ya que solo los números naturales tienen imagen.
Por ejemplo, la sucesión de fracciones (1, 1/2, 1/3, 1/4, 1/5, 1/6, …) se muestra en la siguiente gráfica.
Otra forma común es representar los términos de la sucesión en una recta numérica, esta gráfica nos permite ver "hacia dónde va" la sucesión. Así, la misma secuencia de fracciones se representa de esta forma:
Tipos de sucesiones
Existen diferentes clases de sucesiones, veremos algunas de ellas con ejemplos a continuación.
Sucesiones acotadas
Una sucesión está acotada superiormente (o mayorada) si existe un número real que es mayor o igual que todos los términos de la sucesión. Es decir, ningún término de la sucesión supera ese valor. A ese número se lo llama cota superior. Formalmente, una sucesión (an) está acotada superiormente si existe un número real M tal que an ≤ M para todo n natural.
Una sucesión está acotada inferiormente (o minorada) si existe un número real que es menor o igual que todos los términos de la sucesión. En otras palabras, ningún término de la sucesión es menor que ese valor. A ese número se lo llama cota inferior. Formalmente, una sucesión (an) está acotada inferiormente si existe un número real m tal que an ≥ m para todo n natural.
Una sucesión se dice que está acotada si está acotada inferior y superiormente a la vez, es decir, tiene cota inferior y cota superior. En otras palabras, una sucesión (an) está acotada si existen números reales m y M tales que m ≤ an ≤ M para todo n natural. Todos los términos de la sucesión están comprendidos entre dos valores. A la menor de las cotas superiores se le llama extremo superior o supremo y a la mayor de las cotas inferiores se le llama extremo inferior o ínfimo.
Ejemplos
- (an) = (2, 4, 6, 8, 10, …) es una sucesión acotada inferiormente ya que todos sus términos son mayores o iguales a 2, siendo este valor el ínfimo.
- (bn) = (-1, -2, -3, -4, …) es una sucesión acotada superiormente debido a que todos sus términos son menores o iguales a -1, siendo este el supremo de la sucesión.
- (cn) = (1, 1/2, 1/3, 1/4, 1/5, 1/6, …) es una sucesión acotada ya que todos sus términos se encuentran entre 0 y 1: 0 ≤ cn ≤ 1.
Sucesiones crecientes, decrecientes y monótonas
Una sucesión es creciente si cada término es mayor o igual que el anterior. Es decir, los valores no disminuyen a medida que avanzamos en la sucesión. En símbolos: una sucesión (an) es creciente si ocurre que an+1 ≥ an para todo n natural. La sucesión es estrictamente creciente si cada término es mayor al anterior, en símbolos: an+1 > an para todo n.
Una sucesión es decreciente si cada término es menor o igual que el anterior. Es decir, los valores no aumentan al avanzar en la sucesión. En otros términos: una sucesión (an) es decreciente si ocurre que an+1 ≤ an para todo n natural. La sucesión es estrictamente decreciente si cada término es menor al anterior, en símbolos: an+1 < an para todo n.
Una sucesión es monótona si es creciente o decreciente en todo su dominio. En otras palabras, mantiene siempre el mismo sentido.
Ejemplos
- La sucesión (1, 3, 5, 7, 9, 11, …) es monótona creciente.
- La sucesión (1, 1/2, 1/3, 1/4, 1/5, 1/6, …) es monótona decreciente.
- La sucesión (1, -1, 2, -2, 3, -3,...) no es ni creciente ni decreciente, por tanto, no es monótona.
Sucesiones convergentes
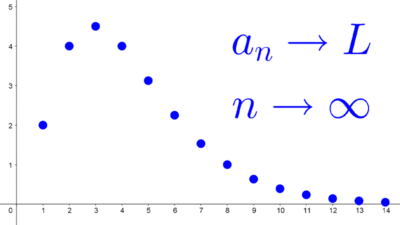
Una sucesión es convergente si, a medida que avanzamos en los términos, sus valores se acercan cada vez más a un número fijo. Ese número se llama límite de la sucesión. Aunque los términos no lleguen a ser exactamente iguales al límite, se acercan tanto como queramos al avanzar hacia el infinito.
Ejemplos
- La sucesión (1, 1/2, 1/3, 1/4, 1/5, 1/6, …) converge a cero porque los términos se acercan cada vez más a ese valor. Esto lo podemos comprobar analizando el término general \(a_n=1/n.\) Cuando \(n → ∞,\) \(a_n → 0.\)
- La sucesión con término general \(a_n=\dfrac{n}{n+1}\) converge a 1 como podemos ver: (1/2, 2/3, 3/4, 4/5, 5/6, 6/7, …). Cuanto más grandes sean los números, más cercano a 1 será el resultado de la división entre el número y su siguiente, por ejemplo, 1000/1001 ≈ 0,999. También podemos analizar el término general dividiendo numerador y denominador entre n: \(a_n=\dfrac{n}{n+1}=\dfrac{n/n}{n/n+1/n}=\dfrac{1}{1+1/n}.\) Cuando \(n → ∞\), \( \dfrac{1}{n} → 0\) provocando que \(a_n → \dfrac{1}{1+0}=1.\)
Determinar si una sucesión converge o no es una cuestión central en el análisis matemático. En ese contexto, existe un teorema útil que establece una condición suficiente para garantizar la convergencia:
Teorema: si una sucesión es monótona y está acotada, entonces es convergente.
Este resultado nos permite concluir que ciertas sucesiones convergen sin necesidad de calcular su límite explícitamente. Además, el teorema se puede enunciar de forma más precisa según el tipo de monotonía:
- Toda sucesión monótona creciente y acotada superiormente es convergente, y su límite es igual al supremo de la sucesión.
- Toda sucesión monótona decreciente y acotada inferiormente es convergente, y su límite es igual al ínfimo de la sucesión.
Es importante destacar que esta condición es suficiente, pero no necesaria. Aunque este teorema nos da una forma práctica de asegurar la convergencia, no implica que toda sucesión convergente deba ser monótona o acotada, ni que el cumplimiento de solo una de esas condiciones sea suficiente:
- Una sucesión puede estar acotada y no converger. Por ejemplo, \((a_n=(-1)^n)\) está acotada entre -1 y 1, pero no converge porque oscila indefinidamente.
- Una sucesión puede no ser monótona y aun así converger. Por ejemplo, \(\left(a_n=\dfrac{(-1)^n}{n}\right)\) no es monótona, pero converge a 0.
- Una sucesión puede ser monótona y no converger si no está acotada. Un ejemplo es la sucesión de Fibonacci, que es creciente pero no acotada, y por lo tanto no converge.
Por otro lado, toda sucesión convergente debe ser acotada. Es decir, la acotación es una condición necesaria para la convergencia, pero no suficiente.
Sucesiones divergentes
Una sucesión divergente es aquella que no se acerca a ningún valor fijo cuando avanzamos hacia términos cada vez mayores. Esto puede ocurrir porque sus términos crecen o decrecen sin límite (tienden a infinito o menos infinito), o porque oscilan entre distintos valores sin estabilizarse en ninguno.
Ejemplos
- La sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, …) es divergente porque sus términos crecen sin límite, se simboliza como \(F_n → ∞.\)
- La sucesión (an = -5n) = (-5, -10, -15, -20, -25, -30, …) es divergente porque sus términos tienden a infinito negativo a medida que n crece: \(a_n → -∞.\)
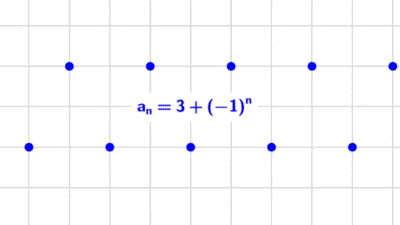
- La sucesión (3 + (-1)n) = (2, 4, 2, 4, 2, …) no converge hacia ningún valor fijo porque sus términos oscilan entre 2 y 4, por tanto, la sucesión es divergente.
Sucesiones oscilantes
Una sucesión oscilante es aquella que no se aproxima a ningún valor determinado ni al infinito, es decir no tiene límite finito ni infinito. En lugar de estabilizarse o crecer sin límite, sus términos cambian entre distintos valores.
Ejemplos
- La sucesión (-1, 1, -1, 1, -1, 1,...) es oscilante porque sus valores alternan entre -1 y 1. Su término general es (-1)n.
- La sucesión (1, 2, 3, 1, 2, 3, 1, 2, 3,...) es oscilante porque repite constantemente los mismos valores.
Nota: en matemáticas de nivel medio es común clasificar las sucesiones en tres tipos: convergentes (si tienen límite finito), divergentes (si tienden al infinito) y oscilantes (si no tienen límite finito ni infinito, sino que sus términos alternan entre distintos valores). Sin embargo, en contextos universitarios más formales, se suele considerar que toda sucesión que no converge es divergente, lo que incluye tanto a las que tienden al infinito como a las que oscilan. En este artículo adoptamos el segundo enfoque.
Otros tipos
- Sucesión alternante: es aquella cuyos términos cambian de signo en forma sucesiva, es decir, positivos y negativos se intercalan. Este tipo de sucesiones pueden converger o no converger. Por ejemplo, la sucesión (1, -1, 1, -1, …) es alternante y diverge mientras que (1, -1/2, 1/3, -1/4, 1/5, -1/6, …) es alternante y converge a cero.
- Sucesión constante: es aquella que tiene todos sus términos iguales, es decir, no cambian a medida que avanza la sucesión. Por ejemplo: (2, 2, 2, 2, …). Una sucesión constante converge al mismo valor que su constante.
- Progresión aritmética: es una sucesión en la que cada término se obtiene sumando un mismo número constante al término anterior. A esa constante se la llama diferencia común. Por ejemplo, la sucesión (3, 7, 11, 15, 19, …) es una sucesión aritmética porque a cada término se le suma 4 para obtener el siguiente; en este caso, la diferencia común es 4.
- Progresión geométrica: es una sucesión en la que cada término se obtiene multiplicando el anterior por una misma constante, llamada razón. Por ejemplo, la sucesión (2, 4, 8, 16, 32, …) es geométrica porque cada término se obtiene multiplicando el anterior por 2.
- Sucesiones iguales: dos sucesiones son iguales si coinciden término a término. Puede ocurrir que dos sucesiones tengan los mismos elementos pero no sean iguales, por ejemplo (1, 0, 1, 0,...) y (0, 1, 0, 1, …) tienen los mismos elementos pero son sucesiones diferentes porque los elementos no están en el mismo orden.
Operaciones con sucesiones
Debido a que las sucesiones son funciones, podemos operarlas entre ellas. Sean (an) = (a1, a2, …) y (bn) = (b1, b2, …) dos sucesiones de números reales, definimos las siguientes operaciones:
| Operación | Definición |
|---|---|
| Valor absoluto | ( |an| ) = (|a1|, |a2|, …) |
| Suma | (an) + (bn) = (an + bn) = (a1 + b1, a2 + b2, …) |
| Resta | (an) - (bn) = (an - bn) = (a1 - b1, a2 - b2, …) |
| Multiplicación | (an) ⋅ (bn) = (an ⋅ bn) = (a1 ⋅ b1, a2 ⋅ b2, …) |
| División | (an) / (bn) = (an / bn) = (a1 / b1, a2 / b2, …) siempre que bn ≠ 0 para toda n. |
Si (an) y (bn) son sucesiones convergentes, entonces:
- La sucesión suma (o resta) (an ± bn) también converge y su límite es la suma (o resta) de los límites.
- La sucesión producto (an ⋅ bn) también converge y el límite es el producto de los límites.
- La sucesión cociente (an / bn) converge y el límite es el cociente de los límites (siempre que el límite de (bn) no sea cero).
Aplicaciones de las sucesiones
Las sucesiones numéricas no solo son herramientas teóricas, sino que también se pueden utilizar para modelar fenómenos reales que evolucionan paso a paso en el tiempo. A continuación veremos tres casos prácticos donde el uso de sucesiones resulta esencial: el crecimiento de una población, el interés compuesto en finanzas y la amortización de deudas.
Crecimiento poblacional
El crecimiento de una población puede modelarse mediante una sucesión geométrica si se asume una tasa de crecimiento constante año tras año.
Ejemplo
Supongamos que una ciudad tiene actualmente 10 000 habitantes y crece a una tasa del 2 % anual. Si denotamos por Pk la población al cabo de k años, entonces:
\(P_k=10 000 \cdot (1,02)^k\)
Los primeros términos de la sucesión serían:
\(P_0=10 000\)
\(P_1=10 000 \cdot 1,02=10 200\)
\(P_2=10 000 \cdot (1,02)^2=10 404\)
y así sucesivamente.
Interés compuesto
En el ámbito financiero, una de las aplicaciones más directas de las sucesiones es el cálculo del interés compuesto, donde el capital inicial genera intereses que se reinvierten, haciendo crecer el monto de forma acumulativa.
Ejemplo
Supongamos que depositamos 5000 dólares en una cuenta bancaria con una tasa del 6 % anual, y no retiramos nada. El capital acumulado al cabo de \(n\) años se puede modelar como:
\(C_n=5 000 \cdot (1,06)^n\)
Esto genera una sucesión del tipo:
5000, 5300, 5618, 5955, …
Cada año, el monto total crece no solo por los intereses sobre el capital inicial, sino también sobre los intereses acumulados de años anteriores. Este es el principio del interés sobre interés.
Amortización de deudas
Cuando se toma un préstamo y se acuerda pagarlo en cuotas fijas periódicas, el capital adeudado disminuye a lo largo del tiempo. Este proceso se puede modelar mediante una sucesión decreciente, que describe el saldo restante después de cada pago.
Ejemplo
Imaginemos que pedimos un préstamo de 100.000 dólares, a devolver en 5 años con una tasa fija del 10 % anual, mediante pagos iguales una vez por año. El saldo de la deuda al final de cada año forma una sucesión que depende tanto del monto abonado como de los intereses generados.
El valor de cada cuota se calcula con una fórmula financiera (por ejemplo, usando anualidades), y el saldo restante al año n, denotado por Dn, se puede expresar de forma recursiva:
\(D_{n+1}=D_n \cdot (1,10)-\text{cuota}\)
Este modelo permite predecir cómo disminuye la deuda con el tiempo y cuánto se paga en intereses en cada periodo.
Recursos adicionales
Graficar una sucesión es muy útil para visualizar su comportamiento, detectar patrones, analizar si converge o diverge, y comparar distintos tipos de crecimiento. Herramientas gratuitas como GeoGebra y Desmos permiten representar sucesiones de forma rápida. A continuación, explicamos paso a paso cómo hacerlo en cada una de estas plataformas.
Graficar en GeoGebra
- Escribir la fórmula de la sucesión como una función de variable real f(x) y ocultar su gráfica.
- Escribir y ejecutar el comando "L = Secuencia(1,100)", esto dará como resultado una lista "L" con los primeros cien números naturales.
- Escribir y ejecutar "(L, f(L))", esto graficará en pantalla los primeros cien puntos de la sucesión.
GeoGebra también permite conocer la lista de términos de una sucesión utilizando este comando:
Secuencia( <Expresión>, <Variable>, <Valor inicial>, <Valor final> )
Por ejemplo, el comando "Secuencia( 1/n, n, 1, 100 )" arrojará una lista con los primeros cien términos de la sucesión con término general 1/n.
Graficar en Desmos
- Escribir la fórmula de la sucesión como una función de variable real f(x) y ocultar su gráfica.
- Escribir y ejecutar "L = [1… 100]", esto dará como resultado una lista "L" con los primeros cien números naturales.
- Escribir y ejecutar "(L, f(L))", esto graficará en pantalla los primeros cien puntos de la sucesión.
Bibliografía
Los siguientes libros fueron consultados para redactar este contenido.
- Apostol, T. (1984). Calculus: cálculo con funciones de una variable, con una introducción al álgebra lineal (2.ª ed.). Editorial Reverté S. A.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9.ª ed.). McGraw-Hill Education.
- Leithold, L. (1994). El cálculo (7.ª ed.). Oxford Educación.
- Rabuffetti, H. (1999). Introducción al análisis matemático: cálculo 1 (15.ª ed.). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable: trascendentes tempranas (7.ª ed.). Cengage Learning.
- Stewart, J., Redlin, L. y Watson, S. (2012). Precálculo: matemáticas para el cálculo (6.ª ed.). Cengage Learning.
- Zill, D. y Wright, W. (2011). Cálculo: trascendentes tempranas (4.ª ed.). McGraw-Hill Education.
Más contenido sobre sucesiones
¿Te ha servido este contenido? ¡Califícalo!
4,8 / 5 — 6 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 27 de julio). Sucesiones numéricas. Dexmath. https://dexmath.com/sucesiones-numericas
2 Comentarios
Deja una respuesta

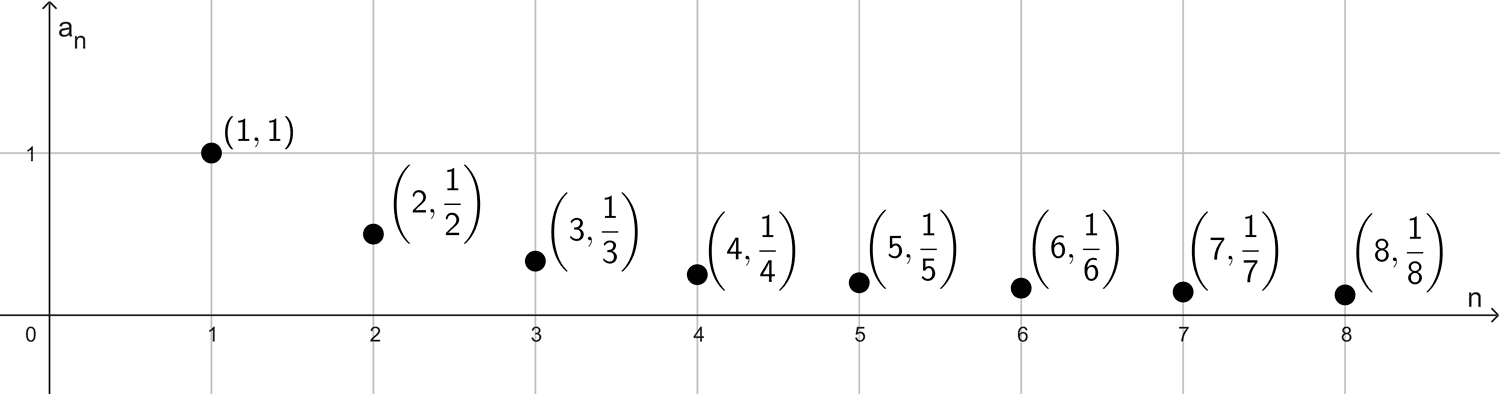

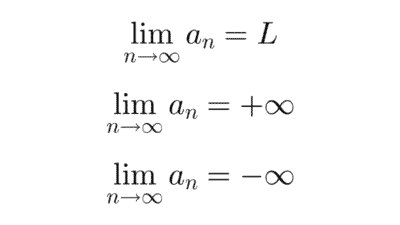

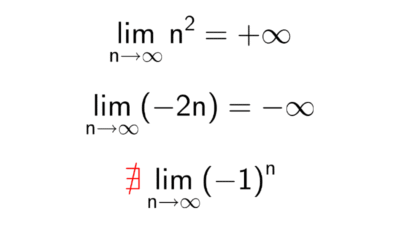
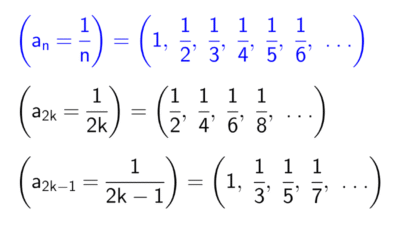
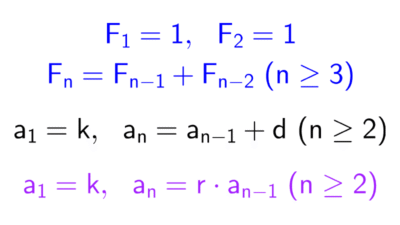
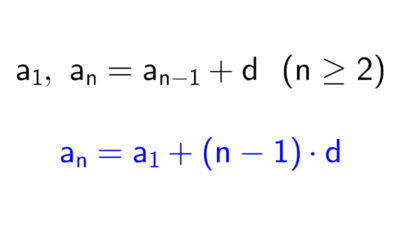
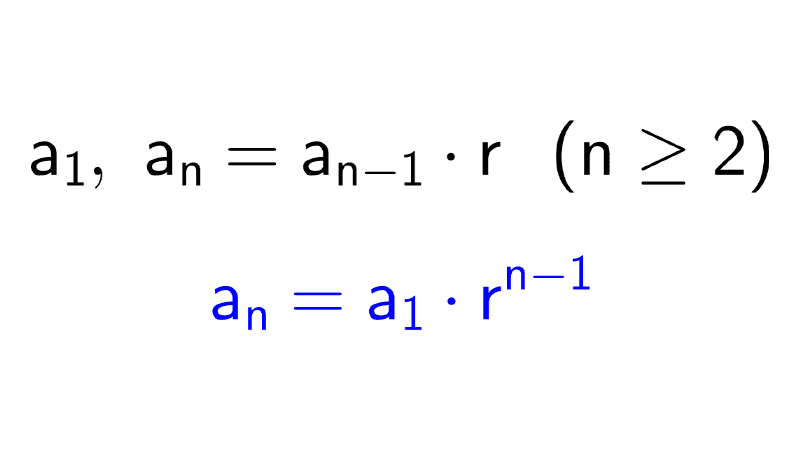
Buen articulo, bien detallado, bien definido para aprender y enseñar las sucesiones